Уравнение движения. Тензор напряжений
При выводе уравнения движения деформируемого твердого тела будем действовать аналогично рассмотренному в разделе 4.3 уравнению движения жидкости и газа. Выделим в деформируемом твердом теле некоторый объем
Напомним, что в правой части уравнения фигурирует полная объемная сила и полная поверхностная сила, возникающая как результат воздействия со стороны пограничных с рассматриваемым объемов. Полная поверхностная сила может быть сведена к объемному интегралу.
где Представим плотность внутренних сил покомпонентно
Тогда
Для того чтобы каждый из трех интегралов в правой части последнего выражения мог быть преобразован в поверхностный, подынтегральную скалярную функцию можно представить в виде дивергенции некоторого вектора
где векторы

Числа
Первый индекс у компонента По аналогии с тензором деформаций тензор напряжений можно разложить на шаровую часть и девиатор
где
Конкретные механические свойства среды, составляющей деформируемое твердое тело, определяются уравнениями, связывающими тензоры напряжений и деформаций, являющиеся аналогами уравнения состояния, задающими свойства газов и жидкостей. Простейшей и широко распространенной моделью деформируемого твердого тела при малых деформациях является закон Гука, формулирующий линейную зависимость между указанными тензорами. При этом удобно использовать раздельные связи между шаровыми и девиаторными составляющими тензоров напряжений и деформаций
 , ,
где постоянные K — модуль объемного сжатия, G — модуль сдвига. Эти характеристики среды связаны с известными из курса «Сопротивление материалов» модулем Юнга E и коэффициентом Пуассона ν соотношениями
Возвращаясь к уравнению движения выделенного объема (64), мы можем теперь представить его правую часть в виде объемных интегралов
Разделим каждое из этих уравнений на
Подставляя эти пределы в предыдущие уравнения и раскрывая выражения для
Наконец вспоминая, что скорость точек тела v связана с перемещением u очевидным образом
Здесь учтено, что при малых деформациях конвективные слагаемые в выражении для полной производной по времени имеют второй порядок малости. Поэтому
|

 , массой Δ m (рис. 25) и запишем для него уравнение второго закона Ньютона, разделяя действующие на него силы на поверхностные и объемные
, массой Δ m (рис. 25) и запишем для него уравнение второго закона Ньютона, разделяя действующие на него силы на поверхностные и объемные

 — поверхностная плотность силы,
— поверхностная плотность силы,  — объемная плотность внутренних сил (сил, действующих между элементами среды внутри выделенного объема). Физическое обоснование преобразования объемного интеграла внутренних сил в поверхностный состоит в том, что для любой пары граничащих друг с другом элементов внутри выделенного объема среды силы взаимного действия их друг на друга равны и противоположны по знаку. Поэтому отличная от нуля составляющая полной поверхностной силы возникает только как результат действия сил со стороны элементов среды, окружающих выделенный объем.
— объемная плотность внутренних сил (сил, действующих между элементами среды внутри выделенного объема). Физическое обоснование преобразования объемного интеграла внутренних сил в поверхностный состоит в том, что для любой пары граничащих друг с другом элементов внутри выделенного объема среды силы взаимного действия их друг на друга равны и противоположны по знаку. Поэтому отличная от нуля составляющая полной поверхностной силы возникает только как результат действия сил со стороны элементов среды, окружающих выделенный объем.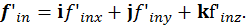
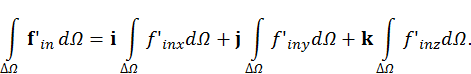
 ,
,  ,
,  ,
, ,
,  ,
,  в проекциях имеют вид
в проекциях имеют вид

 Рис. 32. К определению компонент тензора механических напряжений
Рис. 32. К определению компонент тензора механических напряжений
 образуют матрицу, называемую тензором напряжений
образуют матрицу, называемую тензором напряжений
 , где
, где  — шар:
— шар: ,
,  ,
, — среднее напряжение, равное с обратным знаком гидростатическому давлению.
— среднее напряжение, равное с обратным знаком гидростатическому давлению.  — девиатор
— девиатор .
.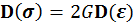 ,
,



 будем иметь
будем иметь
 , получим следующие уравнения
, получим следующие уравнения


 , преобразуем уравнения движения к окончательному виду
, преобразуем уравнения движения к окончательному виду
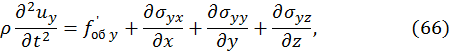

 .
.


