Формирование и распространение ударных волн. Уравнения стационарной ударной волны Рэнкина-Гюгонио
Для слабых возмущений имеем скорость распространения колебаний
или, поскольку где Ударные волны широко распространены в природе. Они формируются при взрывах, при ударах тела о мишень, при мощных импульсных электрических разрядах, при силовом взаимодействии электромагнитного поля со средами. Поскольку на фронте ударной волны имеет место скачек параметров среды (скорости плотности давления, температуры), уравнения гидродинамики могут быть использованы для описания течения до и после скачка. Для того чтобы связать параметры среды до и после фронта ударной волны, следует вернуться к законам сохранения массы, импульса и энергии. Рассмотрим модель стационарного течения за фронтом ударной волны, предполагая, что скорость движения фронта постоянна. Такой режим устанавливается, в частности, при одномерном движении газа в трубе постоянного сечения под действием поршня, движущегося с некоторой постоянной скоростью
 — скорость направленного движения частиц газа (массовая скорость). Если толщина фронта очень мала (в нашей модели она бесконечно мала), то при переходе через него параметры газа меняются скачком (рис. 30). Таким образом, поршень толкает газ, сообщая ему скорость, увеличивая его плотность и внутреннюю энергию в области 1. В рассматриваемой модельной задаче, когда скорость поршня — скорость направленного движения частиц газа (массовая скорость). Если толщина фронта очень мала (в нашей модели она бесконечно мала), то при переходе через него параметры газа меняются скачком (рис. 30). Таким образом, поршень толкает газ, сообщая ему скорость, увеличивая его плотность и внутреннюю энергию в области 1. В рассматриваемой модельной задаче, когда скорость поршня 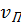 постоянна, и течение является одномерным в области между поршнем и фронтом, параметры среды не изменяются, следовательно, постоянна, и течение является одномерным в области между поршнем и фронтом, параметры среды не изменяются, следовательно, 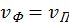 . В общем случае это может не иметь место (например, при точечном взрыве). Однако непосредственно вблизи фронта ударной волны можно установить связь между параметрами среды до и после скачка. Таким образом, результаты, которые будут получены в модели поршня, можно перенести и на более общий случай, понимая под . В общем случае это может не иметь место (например, при точечном взрыве). Однако непосредственно вблизи фронта ударной волны можно установить связь между параметрами среды до и после скачка. Таким образом, результаты, которые будут получены в модели поршня, можно перенести и на более общий случай, понимая под  , скорость течения непосредственно за фронтом ударной волны. Для того чтобы связать параметры среды на скачке воспользуемся основными законами механики. Рассмотрим процесс в системе координат, связанной с фронтом и движущейся со скоростью D, приняв площадь сечения трубы, равной 1. В этой системе наблюдаемая скорость газа есть v–D. За время , скорость течения непосредственно за фронтом ударной волны. Для того чтобы связать параметры среды на скачке воспользуемся основными законами механики. Рассмотрим процесс в системе координат, связанной с фронтом и движущейся со скоростью D, приняв площадь сечения трубы, равной 1. В этой системе наблюдаемая скорость газа есть v–D. За время 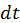 фронт переместится на фронт переместится на 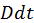 и масса газа и масса газа 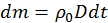 включается в движение за это время и присоединяется к области 2. Наблюдатель в системе координат, связанной с фронтом видит, что его границу в области 2 пересекает поток массы, равный включается в движение за это время и присоединяется к области 2. Наблюдатель в системе координат, связанной с фронтом видит, что его границу в области 2 пересекает поток массы, равный 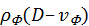 . Приравнивая выражения для одного и того же потока, получим . Приравнивая выражения для одного и того же потока, получим
Это уравнение выражает закон сохранения массы. Закон изменения импульса можно записать в виде
где в левой части записано приращение количества движения, а справа изменения импульса силы. Сокращая на
За время
Равенства (60)–(62) называются уравнениями Рэнкина–Гюгонио. Эти уравнения носят общий характер, т. к. в них использованы только законы сохранения. Из первых двух уравнений имеем
При
Следовательно, ударная волна малой амплитуды есть акустическая (звуковая) волна. Из (61) для акустической волны получаем В качестве примера применения уравнений Рэнкина–Гюгонио рассчитаем скачок давления в воде при падении на ее поверхность плоского твердого тела. При В качестве второго примера применения уравнений Рэнкина–Гюгонио найдем связь давления и плотности за фронтом ударной волны. Для этого к уравнениям (60)–(62) добавим еще и уравнение состояния газа
где s — число степеней свободы молекул газа. Из (60) и (61) получаем
С помощью последнего соотношения и уравнения состояния (63) преобразуем уравнение энергии
откуда можно получить
Эта формула описывает ударную адиабату (адиабату Гюгонио). Ударная адиабата связывает давление и плотность идеального газа при его быстром сжатии в ударной волне. Когда давление в невозмущенном газе много меньше давления за фронтом
|

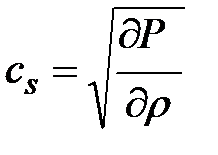 ,
, ,
, 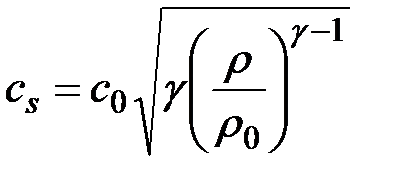 ,
, — скорость звука при нормальной плотности газа. Поскольку показатель адиабаты
— скорость звука при нормальной плотности газа. Поскольку показатель адиабаты 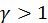 , то чем выше плотность ρ, тем выше
, то чем выше плотность ρ, тем выше 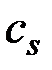 . Если
. Если 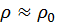 (
(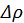 — мало), то влияние изменения плотности в волне на скорость распространения волны незначительно. Ситуация меняется, когда возмущение становится конечным. И хотя анализ, выполненный ранее, относится к малым возмущениям, его можно использовать для качественных рассуждений. Каждой точке среды можно приписать свою локальную скорость звука, пропорциональную, как было показано
— мало), то влияние изменения плотности в волне на скорость распространения волны незначительно. Ситуация меняется, когда возмущение становится конечным. И хотя анализ, выполненный ранее, относится к малым возмущениям, его можно использовать для качественных рассуждений. Каждой точке среды можно приписать свою локальную скорость звука, пропорциональную, как было показано  , которая тем больше, чем выше плотность ρ. Рассмотрим некоторый произвольный профиль волны (рис. 29) в последовательные моменты времени
, которая тем больше, чем выше плотность ρ. Рассмотрим некоторый произвольный профиль волны (рис. 29) в последовательные моменты времени 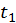 и
и 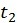 . Приращение плотности, соответствующее точкам N и M, распространяется с различной фазовой скоростью: для точки M она больше, чем для точки N. Поэтому точка M «догоняет» точку N, и вначале пологий фронт волны, по мере ее продвижения становится все более крутым. В пределе фронт превращается в скачок, возникает ударная волна — возмущение конечной амплитуды с крутым профилем плотности и давления. Ударная волна может иметь фронт, реальная толщина которого есть величина порядка длины свободного пробега частиц в газе. Отметим также, что точка M не может перегнать точку N, потому что в этом случае в одной и той же точке среды имело бы место два значения скорости, что не имеет физического смысла в рамках механики сплошной среды, оперирующей усредненными по бесконечно малому объему параметрами вещества.
. Приращение плотности, соответствующее точкам N и M, распространяется с различной фазовой скоростью: для точки M она больше, чем для точки N. Поэтому точка M «догоняет» точку N, и вначале пологий фронт волны, по мере ее продвижения становится все более крутым. В пределе фронт превращается в скачок, возникает ударная волна — возмущение конечной амплитуды с крутым профилем плотности и давления. Ударная волна может иметь фронт, реальная толщина которого есть величина порядка длины свободного пробега частиц в газе. Отметим также, что точка M не может перегнать точку N, потому что в этом случае в одной и той же точке среды имело бы место два значения скорости, что не имеет физического смысла в рамках механики сплошной среды, оперирующей усредненными по бесконечно малому объему параметрами вещества.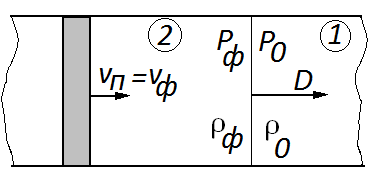 Рис. 30. К выводу уравнений Рэнкина–Гюгонио
Рис. 30. К выводу уравнений Рэнкина–Гюгонио
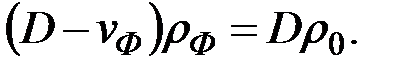 (60)
(60)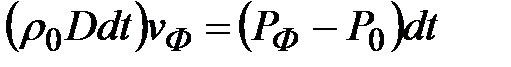 ,
, (61)
(61)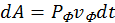 . Частицы, подхваченные поршнем (прошедшие через фронт ударной волны) приобретают направленную скорость
. Частицы, подхваченные поршнем (прошедшие через фронт ударной волны) приобретают направленную скорость  . Кроме того они приобретают еще внутреннюю энергию
. Кроме того они приобретают еще внутреннюю энергию 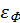 на единицу массы. Таким образом, приращение полной энергии составит
на единицу массы. Таким образом, приращение полной энергии составит 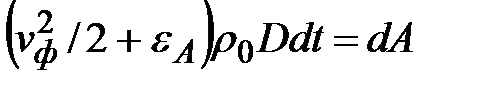 . Приравнивая это приращение к совершенной поршнем работе, получим уравнение энергии для скачка ударной волны
. Приравнивая это приращение к совершенной поршнем работе, получим уравнение энергии для скачка ударной волны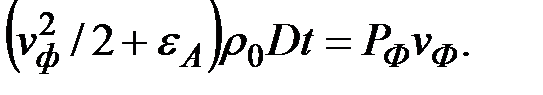 (62)
(62) .
.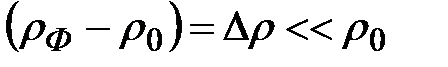 (малые возмущения)
(малые возмущения)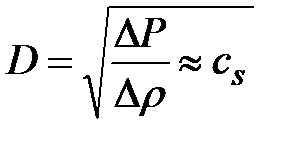 .
. .
.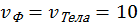 м/с, получим
м/с, получим  (
( кг/м3,
кг/м3, 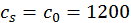 м/с),
м/с), 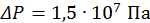 .
.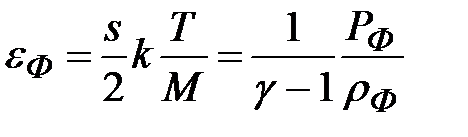 , (63)
, (63)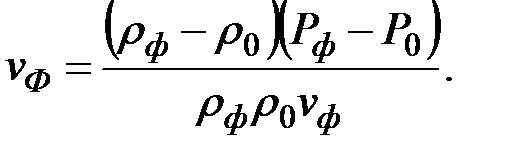
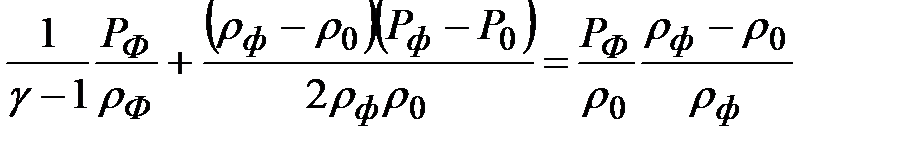 ,
,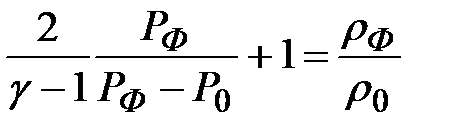 .
.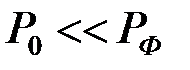 , имеем
, имеем 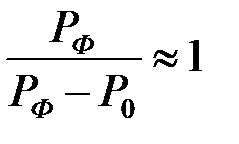 . Тогда при
. Тогда при 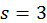 ,
, 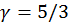 ,
, 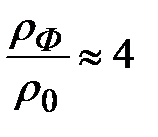 . Это предельная плотность, которая может быть достигнута в одиночной ударной волне. Заметим, что для случая медленного адиабатического сжатия ранее нами было получено выражение, из которого следует непрерывный рост плотности в процессе увеличения давления согласно соотношению
. Это предельная плотность, которая может быть достигнута в одиночной ударной волне. Заметим, что для случая медленного адиабатического сжатия ранее нами было получено выражение, из которого следует непрерывный рост плотности в процессе увеличения давления согласно соотношению 



