Наряду с уравнениями сохранения массы и импульса, которые были использованы выше для вывода уравнений неразрывности и движения, при описании сплошной среды используется также и уравнение энергии. Уравнение энергии рассмотрим для частного случае адиабатического процесса, когда отсутствует теплообмен между элементами сплошной среды. В этом случае изменение внутренней энергии Е элемента сплошной среды с массой  (жидкой частицы) связано только с изменением его объема (при отсутствии объемных источников тепловыделения):
(жидкой частицы) связано только с изменением его объема (при отсутствии объемных источников тепловыделения):  . Вводя в рассмотрение энергию на единицу массы вещества
. Вводя в рассмотрение энергию на единицу массы вещества  , получим
, получим

Поскольку  , то
, то
 .
.
В соответствии с уравнением неразрывности  , поэтому
, поэтому
 .
.
Данное уравнение описывает распределение объемной плотности внутренней энергии 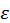 и его изменение, вызываемое деформацией и движением среды. Вместе с тем к изменению внутренней энергии могут приводить процессы, связанные с выделением или поглощением энергии, например при нагреве электрическим током или при химических реакциях. Для учета этих явлений модифицируем последнее уравнение добавлением в его правую часть слагаемого
и его изменение, вызываемое деформацией и движением среды. Вместе с тем к изменению внутренней энергии могут приводить процессы, связанные с выделением или поглощением энергии, например при нагреве электрическим током или при химических реакциях. Для учета этих явлений модифицируем последнее уравнение добавлением в его правую часть слагаемого 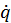 , имеющего размерность Вт/м3, описывающего скорость выделения или поглощения, в зависимости от знака, энергии в точках сплошной среды.
, имеющего размерность Вт/м3, описывающего скорость выделения или поглощения, в зависимости от знака, энергии в точках сплошной среды.
Таким образом, полная система уравнений динамики идеальной жидкости (газа) в адиабатическом режиме имеет вид




Последнее равенство есть уравнение состояния, замыкающее систему и определяющее конкретные физические свойства среды. Приведем примеры уравнения состояния:
1. Идеальный газ:  , где
, где  — постоянная Больцмана, n — концентрация частиц в газе, M — масса частицы.
— постоянная Больцмана, n — концентрация частиц в газе, M — масса частицы.
2. Несжимаемая жидкость: 
3. Вода при высоких давлениях  , где
, где  ,
,  — давление и плотность при нормальных условиях.
— давление и плотность при нормальных условиях.
Последний пример показывает, что для увеличения плотности воды на 20 % необходимо избыточное давление  . Возвращаясь к уравнению энергии, получаем
. Возвращаясь к уравнению энергии, получаем
 ,
,
где вместо  взято произведение концентрации частиц на массу частицы. Частицы газа в общем случае имеют s степеней свободы. На каждую степень свободы при термодинамическом равновесии приходится энергия
взято произведение концентрации частиц на массу частицы. Частицы газа в общем случае имеют s степеней свободы. На каждую степень свободы при термодинамическом равновесии приходится энергия  . Тогда после подстановки выражения для внутренней энергии единицы массы идеального газа
. Тогда после подстановки выражения для внутренней энергии единицы массы идеального газа 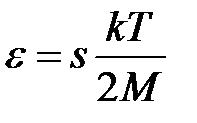 в уравнение энергии получим
в уравнение энергии получим
 ,
,
откуда
 ,
,  ,
,
где 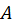 и
и 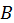 — постоянные. Последнему равенству можно придать вид
— постоянные. Последнему равенству можно придать вид  , где
, где  — показатель адиабаты. Постоянную
— показатель адиабаты. Постоянную 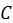 можно определить из начальных условий
можно определить из начальных условий  . В результате уравнение адиабаты получит вид
. В результате уравнение адиабаты получит вид

У газа с тремя степенями свободы  . На практике степенная зависимость давления от плотности, удобная при расчетах, используется для аппроксимации реальных характеристик газов, получаемых экспериментально. Параметр
. На практике степенная зависимость давления от плотности, удобная при расчетах, используется для аппроксимации реальных характеристик газов, получаемых экспериментально. Параметр  при этом называется эффективным показателем адиабаты, а число
при этом называется эффективным показателем адиабаты, а число  — эффективное число степеней свободы. Например, водяной пар при температуре около 10000оК и давлении
— эффективное число степеней свободы. Например, водяной пар при температуре около 10000оК и давлении  Па имеет
Па имеет  . Этому показателю адиабаты соответствует
. Этому показателю адиабаты соответствует  . Столь высокое число степеней свободы свидетельствует о том, что молекулы помимо поступательного движения совершают вращение и испытывают колебания, т. е. у них возбуждены «внутренние» степени свободы.
. Столь высокое число степеней свободы свидетельствует о том, что молекулы помимо поступательного движения совершают вращение и испытывают колебания, т. е. у них возбуждены «внутренние» степени свободы.


 (жидкой частицы) связано только с изменением его объема (при отсутствии объемных источников тепловыделения):
(жидкой частицы) связано только с изменением его объема (при отсутствии объемных источников тепловыделения):  . Вводя в рассмотрение энергию на единицу массы вещества
. Вводя в рассмотрение энергию на единицу массы вещества  , получим
, получим
 , то
, то .
. , поэтому
, поэтому .
.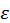 и его изменение, вызываемое деформацией и движением среды. Вместе с тем к изменению внутренней энергии могут приводить процессы, связанные с выделением или поглощением энергии, например при нагреве электрическим током или при химических реакциях. Для учета этих явлений модифицируем последнее уравнение добавлением в его правую часть слагаемого
и его изменение, вызываемое деформацией и движением среды. Вместе с тем к изменению внутренней энергии могут приводить процессы, связанные с выделением или поглощением энергии, например при нагреве электрическим током или при химических реакциях. Для учета этих явлений модифицируем последнее уравнение добавлением в его правую часть слагаемого 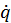 , имеющего размерность Вт/м3, описывающего скорость выделения или поглощения, в зависимости от знака, энергии в точках сплошной среды.
, имеющего размерность Вт/м3, описывающего скорость выделения или поглощения, в зависимости от знака, энергии в точках сплошной среды.


 , где
, где  — постоянная Больцмана, n — концентрация частиц в газе, M — масса частицы.
— постоянная Больцмана, n — концентрация частиц в газе, M — масса частицы.
 , где
, где  ,
,  — давление и плотность при нормальных условиях.
— давление и плотность при нормальных условиях. . Возвращаясь к уравнению энергии, получаем
. Возвращаясь к уравнению энергии, получаем ,
, взято произведение концентрации частиц на массу частицы. Частицы газа в общем случае имеют s степеней свободы. На каждую степень свободы при термодинамическом равновесии приходится энергия
взято произведение концентрации частиц на массу частицы. Частицы газа в общем случае имеют s степеней свободы. На каждую степень свободы при термодинамическом равновесии приходится энергия  . Тогда после подстановки выражения для внутренней энергии единицы массы идеального газа
. Тогда после подстановки выражения для внутренней энергии единицы массы идеального газа 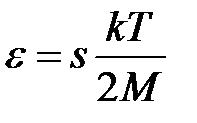 в уравнение энергии получим
в уравнение энергии получим ,
, ,
,  ,
,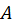 и
и 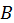 — постоянные. Последнему равенству можно придать вид
— постоянные. Последнему равенству можно придать вид  , где
, где  — показатель адиабаты. Постоянную
— показатель адиабаты. Постоянную 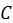 можно определить из начальных условий
можно определить из начальных условий  . В результате уравнение адиабаты получит вид
. В результате уравнение адиабаты получит вид
 . На практике степенная зависимость давления от плотности, удобная при расчетах, используется для аппроксимации реальных характеристик газов, получаемых экспериментально. Параметр
. На практике степенная зависимость давления от плотности, удобная при расчетах, используется для аппроксимации реальных характеристик газов, получаемых экспериментально. Параметр  при этом называется эффективным показателем адиабаты, а число
при этом называется эффективным показателем адиабаты, а число  — эффективное число степеней свободы. Например, водяной пар при температуре около 10000оК и давлении
— эффективное число степеней свободы. Например, водяной пар при температуре около 10000оК и давлении  Па имеет
Па имеет  . Этому показателю адиабаты соответствует
. Этому показателю адиабаты соответствует  . Столь высокое число степеней свободы свидетельствует о том, что молекулы помимо поступательного движения совершают вращение и испытывают колебания, т. е. у них возбуждены «внутренние» степени свободы.
. Столь высокое число степеней свободы свидетельствует о том, что молекулы помимо поступательного движения совершают вращение и испытывают колебания, т. е. у них возбуждены «внутренние» степени свободы.


