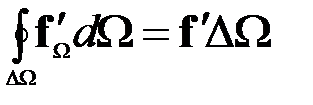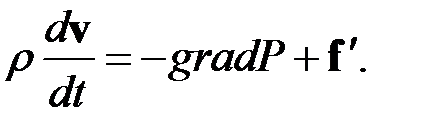УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
Условие сплошности среды означает отсутствие разрывов в ней. Исходя из этого, можно получить уравнение, выражающее собой закон сохранения массы. Для этого в декартовой системе неподвижных (эйлеровых) координат выделим малый элемент в форме параллелепипеда с гранями
 — нормальная составляющая к площадке — нормальная составляющая к площадке  . Масса, вытекающая через противоположную грань, есть . Масса, вытекающая через противоположную грань, есть  . К изменению массы вещества, содержащегося в выделенном элементе пространства приводит разность между втекающей и вытекающей массой. Изменение, обусловленное потоком, вдоль оси x есть . К изменению массы вещества, содержащегося в выделенном элементе пространства приводит разность между втекающей и вытекающей массой. Изменение, обусловленное потоком, вдоль оси x есть
Раскрывая скобки в последнем выражении и пренебрегая слагаемыми высшего порядка малости, получим:
Вычисляя аналогично разности потоков массы через остальные грани, находим полное изменение массы вещества в единицу времени
Откуда, сокращая на
Факт «неразрывности среды», отсутствие скачков потока вещества
Выражение, стоящее слева, определяет полную субстанциональную производную плотности по времени. Поэтому уравнение (53) можно записать, используя полную производную плотности по времени:
В качестве примера, иллюстрирующего физический смысл полной производной Наличие субстанциональной производной характерно для эйлеровой системы отсчета, в которой
где
Пусть элемент среды имеет вид параллелепипеда со сторонами
 и т. д., длины сторон и т. д., длины сторон  , ,  , ,  . При движении элемента среды . При движении элемента среды  , а предел отношения , а предел отношения  при при  есть есть  , где , где  — скорость элемента среды, находящегося в точке с фиксированными (эйлеровыми) координатами — скорость элемента среды, находящегося в точке с фиксированными (эйлеровыми) координатами  . Аналогично преобразуются и другие слагаемые в уравнении (56), и в сумме они дают . Аналогично преобразуются и другие слагаемые в уравнении (56), и в сумме они дают 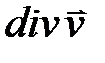 . Закон сохранения массы (55) примет, таким образом, вид . Закон сохранения массы (55) примет, таким образом, вид
Второй член уравнения в полученном уравнении записан уже в эйлеровой системе координат: в нем фигурируют величины
В полученной формуле 4.3. УРАВНЕНИЕ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ Уравнение движения сплошной среды можно получить исходя из второго закона Ньютона. Для этого выделим в движущейся среде элемент объема
Поверхностные силы, напротив, действуют на данный малый элемент среды через его границы. Они могут быть направлены по нормали к данной поверхности (гидростатическое давление) и по касательной к ней (силы трения). В силу того, что произвольно выделенный малый элемент сплошной среды имеет множество возможных направлений нормали и касательной к своей поверхности, для полного описания поверхностных сил следует вводить тензорные величины, характеризующиеся шестью независимыми компонентами, например тензор механических напряжений. В простейшем случае идеальной жидкости, когда внутреннее трение отсутствует, поверхностные силы создаются только гидростатическим давлением и направлены всегда по нормали. Для идеальной жидкости справедлив закон Паскаля: на каждый элемент поверхности S действует сила, направленная по нормали внутрь этой поверхности и равная
Полная поверхностная сила есть
Представим выражение для поверхностной силы в виде
где
В соответствии с теоремой Остроградского–Гаусса для любой векторной величины
где
Полная объемная сила, действующая на выделенный объем, есть
где
При стягивании объема
И с учетом последних выражений получим
Последнее уравнение описывает движение идеальной (невязкой) жидкости.
|

 (рис. 26). Изменение массы вещества в параллелепипеде с объёмом
(рис. 26). Изменение массы вещества в параллелепипеде с объёмом 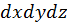 равно
равно  , где
, где  — плотность. Оно обусловлено разностью потоков вещества, втекающего в выделенный объём и вытекающего из него. Рассмотрим эти потоки. Масса вещества, втекающего в единицу времени в данный объем через грань АВСD площадью
— плотность. Оно обусловлено разностью потоков вещества, втекающего в выделенный объём и вытекающего из него. Рассмотрим эти потоки. Масса вещества, втекающего в единицу времени в данный объем через грань АВСD площадью  есть
есть  ,
,  Рис. 26. К выводу уравнения неразрывности в координатах Эйлера
Рис. 26. К выводу уравнения неразрывности в координатах Эйлера



 =0. (53)
=0. (53) существенным образом использован при выводе уравнения (53): только для непрерывной функции
существенным образом использован при выводе уравнения (53): только для непрерывной функции  , имеем
, имеем (53ʹ)
(53ʹ) (54)
(54) , можно рассмотреть стационарный во времени поток, когда
, можно рассмотреть стационарный во времени поток, когда  . Полная производная при этом
. Полная производная при этом  , т. к. изменение параметров элемента среды, находящегося в данной точке эйлеровой системы координат, происходит за счет того, что элемент смещается в эту точку из той, в которой он находился, и где значения дифференцируемого параметра были иными.
, т. к. изменение параметров элемента среды, находящегося в данной точке эйлеровой системы координат, происходит за счет того, что элемент смещается в эту точку из той, в которой он находился, и где значения дифференцируемого параметра были иными. суть координаты точки наблюдения, через которую проходят разные элементы среды. Напротив, в лагранжевой системе отсчета координаты
суть координаты точки наблюдения, через которую проходят разные элементы среды. Напротив, в лагранжевой системе отсчета координаты  характеризуют положение выделенного («окрашенного») элемента жидкости и, если он движется, они зависят от времени. Закон сохранения массы в форме Лагранжа принимает простой вид:
характеризуют положение выделенного («окрашенного») элемента жидкости и, если он движется, они зависят от времени. Закон сохранения массы в форме Лагранжа принимает простой вид: , (55)
, (55) ,
,  — элемент объема. Покажем, что уравнение неразрывности (54) может быть получено из лагранжевой формулировки (55) путем формальных преобразований. После дифференцирования в (55) и деления на
— элемент объема. Покажем, что уравнение неразрывности (54) может быть получено из лагранжевой формулировки (55) путем формальных преобразований. После дифференцирования в (55) и деления на  получим
получим
 ,
,  ,
,  (рис. 27). Тогда
(рис. 27). Тогда . (56)
. (56) Рис. 27. К выводу уравнения неразрывности в координатах Эйлера
Рис. 27. К выводу уравнения неразрывности в координатах Эйлера
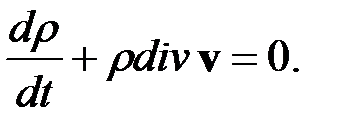
 , относящиеся к фиксированной точке среды, в которой элемент
, относящиеся к фиксированной точке среды, в которой элемент  находится в момент времени t. Сравнивая полученное уравнение и (53ʹ), видим, что субстанциональная производная плотности есть ее полная производная по времени. В этом можно убедиться и другим способом
находится в момент времени t. Сравнивая полученное уравнение и (53ʹ), видим, что субстанциональная производная плотности есть ее полная производная по времени. В этом можно убедиться и другим способом
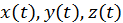 — лагранжевы координаты элемента среды. Таким образом, обе формы закона сохранения массы равноценны.
— лагранжевы координаты элемента среды. Таким образом, обе формы закона сохранения массы равноценны. с фиксированной массой
с фиксированной массой  (рис. 28). Применяя к выделенному (достаточно малому) элементу второй закон Ньютона, запишем:
(рис. 28). Применяя к выделенному (достаточно малому) элементу второй закон Ньютона, запишем: .
. Рис. 28. К выводу уравнения движения сплошной среды
Рис. 28. К выводу уравнения движения сплошной среды
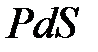 , где P — давление:
, где P — давление:

 ,
, ,
, 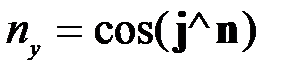 ,
,  . Поэтому выражение для поверхностной силы можно представить как
. Поэтому выражение для поверхностной силы можно представить как . (57)
. (57) справедливо равенство:
справедливо равенство: ,
, — замкнутый объем, ограниченный поверхностью
— замкнутый объем, ограниченный поверхностью  . Применяя последнее свойство векторной величины к каждому слагаемому в правой части (57)
. Применяя последнее свойство векторной величины к каждому слагаемому в правой части (57) =
= .
. ,
, — плотность объемной силы. Уравнение движения теперь принимает вид
— плотность объемной силы. Уравнение движения теперь принимает вид
 ,
,  ,
,