ИСХОДНЫЕ ПОЛОЖЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
Анализ движения отдельных частиц дает наиболее полное описание физической системы. Аппаратом, используемым для такого описания, является кинетическая теория газов. В рамках этой теории на основе решения специальных кинетических уравнений в каждой точке пространства и в каждый момент времени определяется функция распределения по скоростям. По найденной в результате решения кинетического уравнения волновой функции можно найти все необходимые интегральные параметры, такие, как, например, давление, среднюю энергию и т. п. Однако такие задачи являются крайне сложными для аналитического решения. Они сводятся к интегро-дифференциальным с частными производными уравнениям, точное решение которых без заметных упрощений получить не удается. Однако в большом числе практически важных частных случаев возможен упрощенный подход, который реализуется в рамках механики сплошной среды. В этом случае оперируют характеристиками, усредненными по большому числу частиц. Среда может быть описана, как сплошная, если выполнено два условия: - можно ввести понятие физически бесконечно малого объема, - скорость процессов в среде много меньше скорости установления локального (в каждом физически бесконечно малом объеме) термодинамического равновесия с локальными, т. е. зависящими от пространственных координат, параметрами — температура, плотность, давление. Физически бесконечно малый объем обладает размерами намного меньшими размеров области, в которой анализируется движение, и в то же время он содержит много частиц, составляющих среду. При таких условиях столкновения частиц, находящихся в пределах физически бесконечно малого объема быстро приводят к установлению локального термодинамического равновесия. Время установления термодинамического равновесия Критерием возможности использовать понятие физически бесконечно малого объема является соотношение
где В качестве примера рассмотрим течение газа при нормальных условиях, когда концентрация частиц В качестве второго примера рассмотрим течение газа в трубке диаметром 1 см при давлении Подходы Эйлера и Лагранжа к описанию движения сплошной При описании движения сплошной среды существует два метода, один из которых принадлежит Эйлеру, другой — Лагранжу. Метод Эйлера использует фиксированную систему координат. При этом во всех точках пространства в произвольный момент времени наблюдатель фиксирует характеристики течения (скорость, температуру и т. д.) тех элементов среды, которые находятся в этих точках. В методе Лагранжа элементы сплошной среды («жидкие частицы») индивидуализированы. То есть в рамках подхода Лагранжа прослеживается движение и характеристики (скорость, температура и т. д.) каждой частицы. При этом в каждый момент времени могут быть зафиксированы пространственные координаты «жидкой частицы». Индивидуализация «жидких частиц» осуществляется путем задания их начальных координат или, как часто делается при численных расчетах, частицы нумеруются. Сравнивая оба подхода, можно заметить, что эйлеров метод дает меняющуюся во времени пространственную картину процесса, а в лагранжевом подходе определяется «история» каждого фиксированного заранее элемента среды. Первый метод традиционно применяется при аналитическом решении уравнений механики сплошной среды, второй — используется в численных методах. Современные численные методы часто используют комбинацию обоих подходов. Для движения сплошной среды характерно наличие деформации ее элементов («жидких частиц»). Это вносит определенные особенности в уравнения, описывающие движение, хотя при построении системы уравнений механики сплошной среды используются три основных и хорошо известных физических законов сохранения: сохранение массы, импульса и энергии.
|

 по порядку величины совпадает с обратной величиной частоты столкновения
по порядку величины совпадает с обратной величиной частоты столкновения  .
. ,
,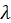 — длина свободного пробега частицы в среде (газе),
— длина свободного пробега частицы в среде (газе),  — характерный размер объема, принятого, как малый, L — характерный размер области движения среды (газа).
— характерный размер объема, принятого, как малый, L — характерный размер области движения среды (газа). при комнатной температуре
при комнатной температуре  . Ранее мы установили, что для таких условий длина свободного пробега частицы газа составит
. Ранее мы установили, что для таких условий длина свободного пробега частицы газа составит  . Средняя скорость теплового движения частиц в воздухе
. Средняя скорость теплового движения частиц в воздухе  . Среднее время между столкновениями составит
. Среднее время между столкновениями составит  . Поэтому для процессов, время протекания которых характеризуется временами
. Поэтому для процессов, время протекания которых характеризуется временами  с и более, существенно меньшее относительно указанного значения время установления локального термодинамического равновесия позволяет применять модель механики сплошной среды. Если характерный размер области течения составляет
с и более, существенно меньшее относительно указанного значения время установления локального термодинамического равновесия позволяет применять модель механики сплошной среды. Если характерный размер области течения составляет  м, то малым с точки зрения анализа течения можно считать объем с линейным размером порядка
м, то малым с точки зрения анализа течения можно считать объем с линейным размером порядка  м, что на два порядка выше длины свободного пробега. Это означает, что выбранный малый объем содержит достаточное число частиц. В нашем случае оно составит около
м, что на два порядка выше длины свободного пробега. Это означает, что выбранный малый объем содержит достаточное число частиц. В нашем случае оно составит около  штук. Таким образом, оба условия применимости модели механики сплошной среды в этом примере оказываются выполненными.
штук. Таким образом, оба условия применимости модели механики сплошной среды в этом примере оказываются выполненными. Па. При таких условиях длина свободного пробега
Па. При таких условиях длина свободного пробега  . Поэтому выделить физически бесконечно малый объем невозможно, так как характерный размер области течения (диаметр трубки) сравним с длиной пробега
. Поэтому выделить физически бесконечно малый объем невозможно, так как характерный размер области течения (диаметр трубки) сравним с длиной пробега 


