РАССЕЯНИЕ ПУЧКА ЧАСТИЦ В СЛОЕ ГАЗА
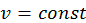 ) поток частиц, причем сечение потока равно единице. Пусть частицы потока движутся вдоль оси ) поток частиц, причем сечение потока равно единице. Пусть частицы потока движутся вдоль оси 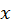 , начало слоя газа совпадает с началом координат (рис. 19). Будем полагать, что любое столкновение приводит к тому, что частица типа 1 покидает поток. , начало слоя газа совпадает с началом координат (рис. 19). Будем полагать, что любое столкновение приводит к тому, что частица типа 1 покидает поток.
Поскольку частицы пучка после столкновения с частицами газа покидают поток, то его изменение в слое газа
Полученное уравнение приводим к виду
После чего его нетрудно проинтегрировать
Поскольку по предположению поток монохроматический,
Таким образом, мы видим, что концентрация убывает по экспоненциальному закону. С помощью полученного распределения концентрации частиц в пучке по координате
Величина
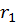 и и 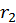 произойдет, если траектории их движения вписываются в цилиндр с радиусом меньшим или равным произойдет, если траектории их движения вписываются в цилиндр с радиусом меньшим или равным 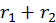 . Поэтому полное сечение столкновения в модели жестких сфер есть . Поэтому полное сечение столкновения в модели жестких сфер есть 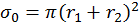 . Рассчитаем с помощью модели жестких сфер длину свободного пробега . Рассчитаем с помощью модели жестких сфер длину свободного пробега 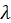 . По определению, на отрезке пути длиной . По определению, на отрезке пути длиной 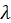 частица 1 испытывает одно столкновение с частицей сорта 2. Поэтому внутри цилиндра, имеющего сечение основания равное частица 1 испытывает одно столкновение с частицей сорта 2. Поэтому внутри цилиндра, имеющего сечение основания равное 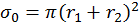 и длину равную и длину равную 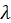 должна находиться ровно одна частица типа 2. Следовательно должна находиться ровно одна частица типа 2. Следовательно 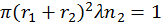 . Отсюда . Отсюда
Полученный результат совпадает с выведенной формулой (44). Выше отмечались характерные условия движения частиц в идеальном газe, при которых размеры частиц много меньше характерных расстояний между ними:
|

 Рис. 19. Рассеяния пучка частиц в слое газа
Рис. 19. Рассеяния пучка частиц в слое газа
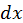 вблизи некоторой точки
вблизи некоторой точки 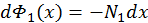 . Подставляя сюда выражение для
. Подставляя сюда выражение для  (43), получим
(43), получим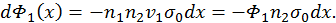
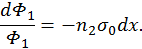
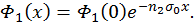
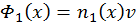 , и последнюю формулу можно переписать для концентрации частиц в пучке
, и последнюю формулу можно переписать для концентрации частиц в пучке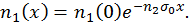
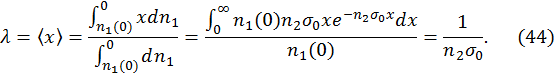
 Рис. 20. Описание столкновения частиц в модели жестких сфер
Рис. 20. Описание столкновения частиц в модели жестких сфер
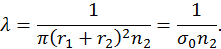
 . Отсюда
. Отсюда  , т. е. длина свободного пробега много больше среднего расстояния между частицами. В воздухе
, т. е. длина свободного пробега много больше среднего расстояния между частицами. В воздухе  м-3,
м-3,  м,
м,  м. Следовательно, условие
м. Следовательно, условие  выполнено.
выполнено.


