СТАТИСТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ГАЗА
Вновь обратимся к формулам для заселенности квантовых состояний, полученным в предыдущем разделе. Оба результата можно представить, как мы это сделали в последнем выражении в виде
Из графиков обеих функций (рис. 15) видно, что при больших значениях энергии Идеальный газ определяется как система свободных невзаимодействующих атомов, находящихся в классическом режиме. Модель идеального газа оказывается весьма плодотворной для целого ряда приложений, включая, газоразрядную плазму, течения и ударные волны в газовых средах. Отсутствие потенциального взаимодействия между частицами идеального газа обуславливает лишь один вид энергии, присущей частицам составляющим газ — кинетическую энергию поступательного движения
Поскольку
где
Формула (36) есть не что иное, как известная функция распределения частиц по скоростям Максвелла. Она дает число частиц в единице объема, обладающих скоростью из интервала
Постоянную
В качестве пределов интегрирования по скоростям в правой части можно выбрать интервалы
Правая часть получившегося выражения содержит произведения трех одинаковых интегралов типа
Для вычисления этого интеграла найдем вначале
Объединяя произведение интегралов в один интеграл по площади в координатах
Поскольку это интеграл по всей плоскости
Теперь
Отсюда найдем постоянную
а распределение Максвелла по скоростям получит свой окончательный вид
Распределение Максвелла можно использовать для нахождения средних значений величин, зависящих от скорости частицы. Пусть имеется некоторая функция скорости
Рассчитаем в качестве примера среднее значение квадрата скорости
Получившийся интеграл представляет собой интеграл по бесконечному объему в пространстве скоростей. При этом интегрируемая функция зависит только от
Теперь задача расчета среднего значения квадрата скорости частиц сводится к вычислению интеграла
Для вычисления интеграла в правой части выражения воспользуемся следующим приемом. Ранее мы нашли
Отсюда имеем в силу четности подынтегральной функции
Дважды продифференцируем полученное выражение по
Таким образом, интеграл в правой части (40) найден, а искомая средняя величина квадрата скорости составит
Аналогичным путем можно найти среднее значение модуля скорости
Для вычисления интеграла в правой части можно использовать новую переменную Заметим, что среднеквадратичная скорость
|


 оба квантовых распределения перестают отличаться друг от друга. Такой режим называется классическим.
оба квантовых распределения перестают отличаться друг от друга. Такой режим называется классическим. . Как было сказано выше, в классическом режиме квантовые распределения перестают отличаться друг от друга, следовательно, единицей в знаменателе (35) можно пренебречь. В результате имеем
. Как было сказано выше, в классическом режиме квантовые распределения перестают отличаться друг от друга, следовательно, единицей в знаменателе (35) можно пренебречь. В результате имеем
 ,
,  ,
,  последнее выражение приводится к виду
последнее выражение приводится к виду




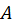 в (36) можно найти, если задаться концентрацией частиц идеального газа (
в (36) можно найти, если задаться концентрацией частиц идеального газа (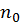 ) — полным числом частиц в единице объема. Тогда, интегрируя (36) слева и справа, получим
) — полным числом частиц в единице объема. Тогда, интегрируя (36) слева и справа, получим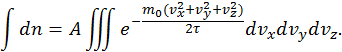
 . Несмотря на то, что всякая скорость не может превосходить скорость света, использование бесконечных скоростей в правой части последнего выражения не приведет к ошибке, так как оно содержит быстро затухающую функцию скорости. Принимая во внимание, что слева в последней формуле стоит интеграл от полного дифференциала, и разбивая экспоненту в правой части на три сомножителя, получим
. Несмотря на то, что всякая скорость не может превосходить скорость света, использование бесконечных скоростей в правой части последнего выражения не приведет к ошибке, так как оно содержит быстро затухающую функцию скорости. Принимая во внимание, что слева в последней формуле стоит интеграл от полного дифференциала, и разбивая экспоненту в правой части на три сомножителя, получим

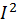 :
:
 ,
,  , получим
, получим
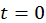 ,
,  , при этом радиальная координата ρ связана с декартовыми
, при этом радиальная координата ρ связана с декартовыми  , а элемент площади интегрирования
, а элемент площади интегрирования  равен
равен  . В результате получим
. В результате получим
 . Используя этот результат, вычислим правую часть (38)
. Используя этот результат, вычислим правую часть (38)


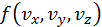 , тогда ее среднее значение будет найдено по формуле
, тогда ее среднее значение будет найдено по формуле
 . При этом получим
. При этом получим
 , следовательно, обладает сферической симметрией по отношению к точке
, следовательно, обладает сферической симметрией по отношению к точке  . Поэтому для интегрирования удобно использовать сферические координаты, в которых радиальная координата есть
. Поэтому для интегрирования удобно использовать сферические координаты, в которых радиальная координата есть  , а элемент объема
, а элемент объема



 :
: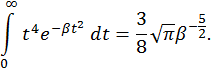


 .
. и полученная здесь средняя скорость
и полученная здесь средняя скорость  отличатся множителем 1, 178, т. е. практически равны. В следующем разделе будет показано, что энергетическая температура
отличатся множителем 1, 178, т. е. практически равны. В следующем разделе будет показано, что энергетическая температура  связана с термодинамической соотношением
связана с термодинамической соотношением  , где
, где  Дж/K. Поэтому приведенные формулы можно применять для вычисления тепловой скорости частиц в газах. В частности для кислорода (
Дж/K. Поэтому приведенные формулы можно применять для вычисления тепловой скорости частиц в газах. В частности для кислорода (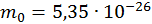 кг – масса молекулы) при комнатной температуре
кг – масса молекулы) при комнатной температуре  K, средняя тепловая скорость составит 480 м/с.
K, средняя тепловая скорость составит 480 м/с.


