Значения энергии U и числа частиц N для различных состояний системы бозонов
Для всех приложений величина
Для вычисления суммы в числителе последнего выражения продифференцируем сумму Гиббса по
Отсюда легко находим
Поскольку для суммы Гиббса аналитическое выражение нами было найдено, то
Для средней заселенности, таким образом, имеем
Полученное выражение носит название распределения Бозе–Эйнштейна. От полученного ранее распределения Ферми–Дирака эта формула отличается знаком перед единицей в знаменателе. График зависимости < N> от энергии бозона E построен на рис. 15. Итак, мы получили формулы, для подсчета средней заселенности состояния с энергией
Реальное движение частиц является трехмерным. Нетрудно на основе решения уравнения Шредингера показать, что если частица заперта в трехмерной кубической области с длиной ребра l, энергетический спектр рассчитывается по той же формуле, с той разницей, что
где
Нетрудно видеть, что минимально возможная величина, на которую может изменяться проекция импульса на ось координат будет
Поэтому минимальный размер квантовой ячейки в пространстве импульсов составит
а количество ячеек в пространстве импульсов (состояний), приходящихся на единичный интервал изменения импульса, составит
Примем к сведению, что сама по себе частица может находиться в различных внутренних квантовых состояния, например, электрон имеет два внутренних собственных квантовых состояния со значением проекции спина ½ и –½. Если обозначить число внутренних квантовых состояний частицы как
В этом разделе мы увидели, что не все состояния заселены частицами одинаково. Степень заселенности состояния вычисляется с помощью полученных выше функций распределения. Поэтому, составляя выражение для полного числа частиц, обладающих импульсом из малого интервала его изменения, мы должны умножить количество квантовых состояний, приходящихся на этот интервал, и на заселенность этих состояний. Для определения малой величины изменения импульса заметим, что в системах содержащих большое количество частиц, несмотря на то, что все характеристики движения частиц, включая импульс, образуют дискретный спектр значений, квант дискретизации весьма мал, по сравнению с самим значением того же импульса. Это позволяет пренебречь дискретностью и пользоваться математическими формулами и методами для непрерывных величин. Поэтому малый интервал изменения импульса можно записать в форме
где знак «+» берется для фермионов, а «–» — для бозонов. Если в последней формуле перейти от полного числа частиц к расчету их в единице объема, то поделив (34) на объем
Здесь величина
|

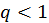 , так как иначе число бозонов в системе нельзя было бы считать неограниченным из-за расходимости суммы, что не соответствовало бы свойствам, характерным для бозонов. Среднее значение заселенности найдем по правилу нахождения средних по ансамблю
, так как иначе число бозонов в системе нельзя было бы считать неограниченным из-за расходимости суммы, что не соответствовало бы свойствам, характерным для бозонов. Среднее значение заселенности найдем по правилу нахождения средних по ансамблю
 :
:

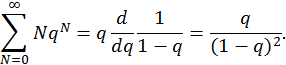

 для частиц, обладающих различными квантовыми свойствами (бозоны и фермионы). Рассмотрим другую задачу. Подсчитаем количество частиц, имеющих импульс, принадлежащий малому интервалу вблизи значения
для частиц, обладающих различными квантовыми свойствами (бозоны и фермионы). Рассмотрим другую задачу. Подсчитаем количество частиц, имеющих импульс, принадлежащий малому интервалу вблизи значения  ,
,  ,
,  . Ранее в разделе 1.3 мы с помощью уравнении Шредингера рассмотрели одномерное движение частицы в потенциальной яме шириной
. Ранее в разделе 1.3 мы с помощью уравнении Шредингера рассмотрели одномерное движение частицы в потенциальной яме шириной 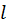 . При этом был вычислен энергетический спектр частицы
. При этом был вычислен энергетический спектр частицы
 ,
, ,
,  ,
,  — независимые квантовые целые числа, каждое из которых меняется как 1, 2, …∞. Выражение для проекций импульса на оси координат следуют из формулы
— независимые квантовые целые числа, каждое из которых меняется как 1, 2, …∞. Выражение для проекций импульса на оси координат следуют из формулы  :
: ,
, 
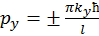 ,
, 
 ,
, 


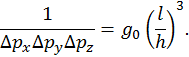
 – внутренний фактор вырождения, то формулу для числа квантовых состояний, приходящихся на единичный интервал изменения импульса, следует переписать как
– внутренний фактор вырождения, то формулу для числа квантовых состояний, приходящихся на единичный интервал изменения импульса, следует переписать как . Теперь запишем выражения для числа частиц, имеющих импульс из указанного малого интервала изменения
. Теперь запишем выражения для числа частиц, имеющих импульс из указанного малого интервала изменения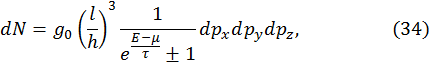
 , получим
, получим
 — число частиц, приходящееся на единицу объема.
— число частиц, приходящееся на единицу объема.


