КВАНТОВЫЕ СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
Из предыдущих разделов известно, что любая квантовая система предоставляет частицам, ее составляющим, занимать разрешенные квантовые состояния. Число и параметры этих состояний зависят от конкретного устройства системы и, в частности, от природы самих частиц. Поставим задачу вычисления средней заселенности некоторого квантового состояния, которое характеризуется энергией Для подсчета средних значений будем использовать общий подход, который при расчете средней по ансамблю величины параметра, принимающего значение
где суммирование ведется по всем возможным значениям индекса
Как было установлено в разделе 1.6, все частицы подразделяются на два сорта — фермионы, на которые распространяется принцип запрета Паули, и бозоны, не подчиняющиеся принципу запрета. Очевидно, что результаты подсчета средней заселенности энергетического состояния для частиц разных типов будут различны. Начнем с фермионов. Некоторое состояние может быть либо свободным, в этом случае ввиду отсутствия частицы и энергия равна нулю, либо занято одной частицей, при этом энергию частицы обозначим
Соответствующая сумма Гиббса будет равна
Средняя заселенность
Подставляя сюда найденное выражение для суммы Гиббса, после элементарных преобразований найдем среднюю по ансамблю заселенность состояния с энергией
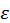 приведен на рис. 15. Обратим внимание на то, что при температуре приведен на рис. 15. Обратим внимание на то, что при температуре  , стремящейся к нулю, все состояния с энергией ниже некоторого уровня , стремящейся к нулю, все состояния с энергией ниже некоторого уровня 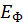 , оказываются заняты фермионами < N> =1, а заселенность состояний с , оказываются заняты фермионами < N> =1, а заселенность состояний с 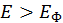 равна нулю. Данное значение энергии называется энергией Ферми. С ростом температуры доля состояний с равна нулю. Данное значение энергии называется энергией Ферми. С ростом температуры доля состояний с 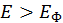 начинает расти, за счет снижения заселенности состояний с энергий меньшей энергии Ферми (рис. 15). начинает расти, за счет снижения заселенности состояний с энергий меньшей энергии Ферми (рис. 15).
Рассмотрим теперь заселенность состояния с энергией
где Таблица 2
|

 . Под средней заселенностью подразумевается среднее число частиц, обладающих указанной энергией.
. Под средней заселенностью подразумевается среднее число частиц, обладающих указанной энергией. с вероятностью
с вероятностью  , сводится к формуле:
, сводится к формуле: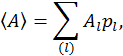
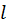 , т. е. с учетом всех возможных значений параметра
, т. е. с учетом всех возможных значений параметра 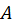 . Формулу для вероятности состояния системы, состоящей из частиц, мы вывели в предыдущем разделе. Поэтому последнюю формулу можем переписать в виде
. Формулу для вероятности состояния системы, состоящей из частиц, мы вывели в предыдущем разделе. Поэтому последнюю формулу можем переписать в виде
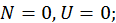
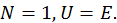
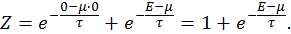
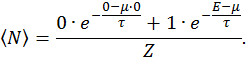
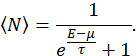
 Рис. 15. Распределение Ферми–Дирака (1) и Бозе–Эйнштейна (2)
Рис. 15. Распределение Ферми–Дирака (1) и Бозе–Эйнштейна (2)
 и числа частиц
и числа частиц  для различных состояний системы бозонов (табл. 2). Таким образом, если в системе пребывает
для различных состояний системы бозонов (табл. 2). Таким образом, если в системе пребывает  бозонов, то ее энергия
бозонов, то ее энергия  . Поэтому большая сумма Гиббса будет содержать бесконечное число слагаемых
. Поэтому большая сумма Гиббса будет содержать бесконечное число слагаемых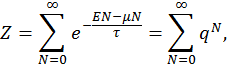
 . При условии
. При условии 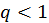 последняя сумма будет сходящейся как бесконечная геометрическая прогрессия со знаменателем меньшим 1 —
последняя сумма будет сходящейся как бесконечная геометрическая прогрессия со знаменателем меньшим 1 —  .
.


