 Рис. 16. К выводу формулы давления идеального газа
Рис. 16. К выводу формулы давления идеального газа
|
Рассчитаем давление, создаваемое идеальным газом, находящимся при температуре

, при концентрации частиц
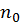
. По определению давление является силой, действующей на единицу площади поверхности. Рассмотрим плоскую стенку сосуда, перпендикулярную оси
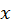
(рис.1 6). Сила, с которой газ действует на стенку, возникает в результате ударов частиц, составляющих газ. Из стандартного соотношения механики
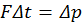
, где
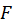
— вектор силы,
p — импульс, мы можем заключить, что сила, действующая на стенку, равна импульсу, передаваемому ей частицами за единицу времени. Для выбранной стенки (рис. 16) нас будет интересовать проекция вектора импульса на ось
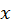
.
Частица газа, совершая упругое столкновение со стенкой, изменяет свою скорость с  на
на  . При этом ее импульс изменяется на величину
. При этом ее импульс изменяется на величину  . Таким образом, при одном ударе частицы стенке передается импульс, равный
. Таким образом, при одном ударе частицы стенке передается импульс, равный  . Рассчитаем, сколько таких ударов придется на единицу поверхности стенки за 1 с. Найденная величина и будет давлением газа на стенку. Выделим на поверхности стенки участок площадью 1 м2 (рис. 16). Построим на этом участке площади, как на основании цилиндр, высота которого численно равна
. Рассчитаем, сколько таких ударов придется на единицу поверхности стенки за 1 с. Найденная величина и будет давлением газа на стенку. Выделим на поверхности стенки участок площадью 1 м2 (рис. 16). Построим на этом участке площади, как на основании цилиндр, высота которого численно равна  . При таком выборе высоты цилиндра все частицы, в нем заключающиеся, в течение единицы времени достигнут поверхности стенки, т. е. за единицу времени на единице поверхности стенки произойдет
. При таком выборе высоты цилиндра все частицы, в нем заключающиеся, в течение единицы времени достигнут поверхности стенки, т. е. за единицу времени на единице поверхности стенки произойдет  ударов. Поэтому за единицу времени стенке будет предан импульс
ударов. Поэтому за единицу времени стенке будет предан импульс  . По сути дела мы нашли давление, которое создавали бы частицы, летящие с некоторой фиксированной скоростью
. По сути дела мы нашли давление, которое создавали бы частицы, летящие с некоторой фиксированной скоростью  . Нам, однако, известно, что на самом деле скорости частиц разные и подчинены распределению Максвелла. Поэтому для расчета давления нам потребуется проинтегрировать найденную величину по всем скоростям с учетом их доли в общем распределении Максвелла
. Нам, однако, известно, что на самом деле скорости частиц разные и подчинены распределению Максвелла. Поэтому для расчета давления нам потребуется проинтегрировать найденную величину по всем скоростям с учетом их доли в общем распределении Максвелла
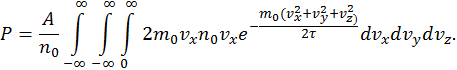
Следует обратить внимание на то, что нижний предел интегрирования по  взят равным нулю, а не минус бесконечности, поскольку нас интересуют только положительные проекции
взят равным нулю, а не минус бесконечности, поскольку нас интересуют только положительные проекции  , приводящие к столкновению со стенкой (рис. 16). Разбивая экспоненту на сомножители, получим
, приводящие к столкновению со стенкой (рис. 16). Разбивая экспоненту на сомножители, получим

Выражение для первых двух интегралов в правой части последней формулы было найдено нами ранее:  . Для вычисления третьего интеграла выполним однократное дифференцирование (41) по параметру
. Для вычисления третьего интеграла выполним однократное дифференцирование (41) по параметру  . При этом получим
. При этом получим
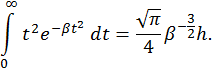
Подставляя значения интегралов и постоянной 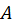 в выражение для давления, найдем
в выражение для давления, найдем
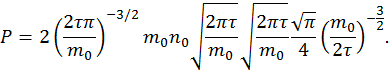
После упрощения выражения получим
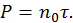
Из общего курса физики хорошо известна формула для расчета давления идеального газа  , где
, где  Дж/K — постоянная Больцмана,
Дж/K — постоянная Больцмана,  — абсолютная температура. Сравнивая с полученной нами формулой, находим связь между введенной нами энергетической температурой
— абсолютная температура. Сравнивая с полученной нами формулой, находим связь между введенной нами энергетической температурой  и термодинамической температурой
и термодинамической температурой  :
:  . Существенно отметить, что сделанный нами вывод закона для давления идеального газа проистекает из самых общих положений квантовой статистики и не использует каких-либо опытных данных.
. Существенно отметить, что сделанный нами вывод закона для давления идеального газа проистекает из самых общих положений квантовой статистики и не использует каких-либо опытных данных.
 , при концентрации частиц
, при концентрации частиц 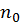 . По определению давление является силой, действующей на единицу площади поверхности. Рассмотрим плоскую стенку сосуда, перпендикулярную оси
. По определению давление является силой, действующей на единицу площади поверхности. Рассмотрим плоскую стенку сосуда, перпендикулярную оси 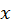 (рис.1 6). Сила, с которой газ действует на стенку, возникает в результате ударов частиц, составляющих газ. Из стандартного соотношения механики
(рис.1 6). Сила, с которой газ действует на стенку, возникает в результате ударов частиц, составляющих газ. Из стандартного соотношения механики 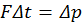 , где
, где 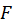 — вектор силы, p — импульс, мы можем заключить, что сила, действующая на стенку, равна импульсу, передаваемому ей частицами за единицу времени. Для выбранной стенки (рис. 16) нас будет интересовать проекция вектора импульса на ось
— вектор силы, p — импульс, мы можем заключить, что сила, действующая на стенку, равна импульсу, передаваемому ей частицами за единицу времени. Для выбранной стенки (рис. 16) нас будет интересовать проекция вектора импульса на ось 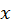 .
.

 Рис. 16. К выводу формулы давления идеального газа
Рис. 16. К выводу формулы давления идеального газа
 на
на  . При этом ее импульс изменяется на величину
. При этом ее импульс изменяется на величину  . Таким образом, при одном ударе частицы стенке передается импульс, равный
. Таким образом, при одном ударе частицы стенке передается импульс, равный  . Рассчитаем, сколько таких ударов придется на единицу поверхности стенки за 1 с. Найденная величина и будет давлением газа на стенку. Выделим на поверхности стенки участок площадью 1 м2 (рис. 16). Построим на этом участке площади, как на основании цилиндр, высота которого численно равна
. Рассчитаем, сколько таких ударов придется на единицу поверхности стенки за 1 с. Найденная величина и будет давлением газа на стенку. Выделим на поверхности стенки участок площадью 1 м2 (рис. 16). Построим на этом участке площади, как на основании цилиндр, высота которого численно равна  ударов. Поэтому за единицу времени стенке будет предан импульс
ударов. Поэтому за единицу времени стенке будет предан импульс  . По сути дела мы нашли давление, которое создавали бы частицы, летящие с некоторой фиксированной скоростью
. По сути дела мы нашли давление, которое создавали бы частицы, летящие с некоторой фиксированной скоростью 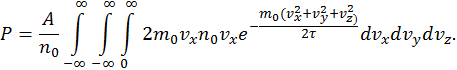

 . Для вычисления третьего интеграла выполним однократное дифференцирование (41) по параметру
. Для вычисления третьего интеграла выполним однократное дифференцирование (41) по параметру  . При этом получим
. При этом получим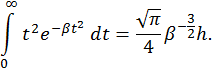
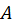 в выражение для давления, найдем
в выражение для давления, найдем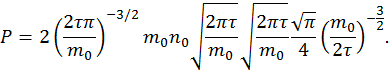
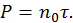
 , где
, где  Дж/K — постоянная Больцмана,
Дж/K — постоянная Больцмана,  — абсолютная температура. Сравнивая с полученной нами формулой, находим связь между введенной нами энергетической температурой
— абсолютная температура. Сравнивая с полученной нами формулой, находим связь между введенной нами энергетической температурой  . Существенно отметить, что сделанный нами вывод закона для давления идеального газа проистекает из самых общих положений квантовой статистики и не использует каких-либо опытных данных.
. Существенно отметить, что сделанный нами вывод закона для давления идеального газа проистекает из самых общих положений квантовой статистики и не использует каких-либо опытных данных.


