 Рис. 18. Отклонение частицы 1 при столкновении с частицей 2 в малый телесный угол
Рис. 18. Отклонение частицы 1 при столкновении с частицей 2 в малый телесный угол 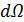
|
Основным физическим эффектом в газах являются столкновения частиц, составляющих газ. Переход газа от неравновесного состояния к равновесному осуществляется благодаря большому количеству актов взаимодействия частиц, происходящих на малом расстоянии между ними. Учитывая, что размеры частиц намного меньше среднего расстояния между ними, эти взаимодействия можно трактовать, как столкновения. В газах среднее расстояние между частицами можно оценить как
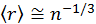
. Характерным для газов является то, что
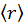
много больше величины
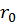
— расстояния на котором происходит взаимодействие. В электрически нейтральных газах частицы в промежутках между столкновениями движутся по прямой линии. Поэтому траектория движения частицы газа близка по форме к ломаной линии. Наиболее вероятным взаимодействием в газе являются парные столкновения, т. е. взаимодействия двух частиц.
Рассмотрим следующую модельную задачу. Пусть имеется пучок частиц с концентрацией 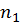 и скоростью
и скоростью 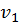 . Частицы пучка сталкиваются с неподвижными частицами (мишенями), концентрация которых равна
. Частицы пучка сталкиваются с неподвижными частицами (мишенями), концентрация которых равна  . В результате столкновений частицы первого типа рассеиваются, т. е. изменяют направление своего движения на некоторый угол. Предположим, что частицы-мишени достаточно малы и частица пучка может испытать не более одного столкновения. Разместим в области частиц мишеней начало сферической системы координат и рассчитаем долю частиц пучка, отклонившихся в результате столкновений в малый телесный угол
. В результате столкновений частицы первого типа рассеиваются, т. е. изменяют направление своего движения на некоторый угол. Предположим, что частицы-мишени достаточно малы и частица пучка может испытать не более одного столкновения. Разместим в области частиц мишеней начало сферической системы координат и рассчитаем долю частиц пучка, отклонившихся в результате столкновений в малый телесный угол  (рис. 18). Число частиц типа 1 (частицы пучка), рассеянных в элемент телесного угла
(рис. 18). Число частиц типа 1 (частицы пучка), рассеянных в элемент телесного угла 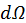 при столкновении с частицами типа 2 (частицы мишени) в единице объема за единицу времени, пропорционально числу частиц-мишеней в единице объема
при столкновении с частицами типа 2 (частицы мишени) в единице объема за единицу времени, пропорционально числу частиц-мишеней в единице объема  , числу частиц пучка, поступающих в единицу объема за единицу времени
, числу частиц пучка, поступающих в единицу объема за единицу времени 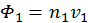 , а также самому телесному углу:
, а также самому телесному углу:
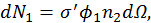
где коэффициент пропорциональности 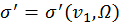 имеет размерность площади и в общем случае зависит от скорости сближения частиц, в нашей задаче это
имеет размерность площади и в общем случае зависит от скорости сближения частиц, в нашей задаче это 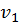 , и от угла рассеяния
, и от угла рассеяния  . Величина
. Величина 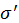 зависит от сорта частиц и характеризует конкретную природу их взаимодействия. Величина
зависит от сорта частиц и характеризует конкретную природу их взаимодействия. Величина 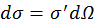 носит название дифференциального сечения рассеяния в элемент телесного угла
носит название дифференциального сечения рассеяния в элемент телесного угла 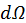 . Можно дать геометрическую трактовку дифференциального сечения рассеяния, как плоскость проекции мишени на плоскость, перпендикулярную вектору скорости сближения
. Можно дать геометрическую трактовку дифференциального сечения рассеяния, как плоскость проекции мишени на плоскость, перпендикулярную вектору скорости сближения 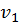 , попадание в которую приводит к отклонению в телесный угол
, попадание в которую приводит к отклонению в телесный угол 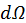 .
.
Рассмотрим, когда скорость падающих частиц одинакова, а 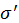 не зависит от угла
не зависит от угла 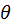 . Тогда полное число частиц, рассеянное в телесный угол 4π за 1 с в расчете на 1 м3, составит
. Тогда полное число частиц, рассеянное в телесный угол 4π за 1 с в расчете на 1 м3, составит
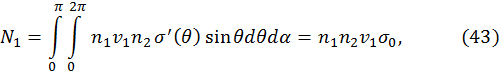
где 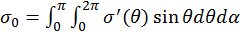 — полное сечение рассеяния. Величина
— полное сечение рассеяния. Величина 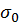 характеризует интегральный эффект, т. е. полное число частиц, покидающий поток за единицу времени в единице объема. Геометрическая интерпретация полного сечения — это площадь мишени, соответствующей одной частице типа 2. Численное значение сечения для электрически нейтральных частиц имеет порядок
характеризует интегральный эффект, т. е. полное число частиц, покидающий поток за единицу времени в единице объема. Геометрическая интерпретация полного сечения — это площадь мишени, соответствующей одной частице типа 2. Численное значение сечения для электрически нейтральных частиц имеет порядок  м2.
м2.
В предположении, что 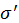 не зависит от угла
не зависит от угла 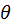 , получаем
, получаем 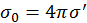 . Откуда
. Откуда 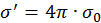 . Параметр
. Параметр 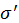 называется сечением рассеяния в единицу телесного угла.
называется сечением рассеяния в единицу телесного угла.
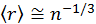 . Характерным для газов является то, что
. Характерным для газов является то, что 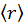 много больше величины
много больше величины 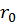 — расстояния на котором происходит взаимодействие. В электрически нейтральных газах частицы в промежутках между столкновениями движутся по прямой линии. Поэтому траектория движения частицы газа близка по форме к ломаной линии. Наиболее вероятным взаимодействием в газе являются парные столкновения, т. е. взаимодействия двух частиц.
— расстояния на котором происходит взаимодействие. В электрически нейтральных газах частицы в промежутках между столкновениями движутся по прямой линии. Поэтому траектория движения частицы газа близка по форме к ломаной линии. Наиболее вероятным взаимодействием в газе являются парные столкновения, т. е. взаимодействия двух частиц.

 Рис. 18. Отклонение частицы 1 при столкновении с частицей 2 в малый телесный угол
Рис. 18. Отклонение частицы 1 при столкновении с частицей 2 в малый телесный угол 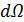
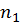 и скоростью
и скоростью 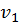 . Частицы пучка сталкиваются с неподвижными частицами (мишенями), концентрация которых равна
. Частицы пучка сталкиваются с неподвижными частицами (мишенями), концентрация которых равна  . В результате столкновений частицы первого типа рассеиваются, т. е. изменяют направление своего движения на некоторый угол. Предположим, что частицы-мишени достаточно малы и частица пучка может испытать не более одного столкновения. Разместим в области частиц мишеней начало сферической системы координат и рассчитаем долю частиц пучка, отклонившихся в результате столкновений в малый телесный угол
. В результате столкновений частицы первого типа рассеиваются, т. е. изменяют направление своего движения на некоторый угол. Предположим, что частицы-мишени достаточно малы и частица пучка может испытать не более одного столкновения. Разместим в области частиц мишеней начало сферической системы координат и рассчитаем долю частиц пучка, отклонившихся в результате столкновений в малый телесный угол  (рис. 18). Число частиц типа 1 (частицы пучка), рассеянных в элемент телесного угла
(рис. 18). Число частиц типа 1 (частицы пучка), рассеянных в элемент телесного угла 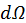 при столкновении с частицами типа 2 (частицы мишени) в единице объема за единицу времени, пропорционально числу частиц-мишеней в единице объема
при столкновении с частицами типа 2 (частицы мишени) в единице объема за единицу времени, пропорционально числу частиц-мишеней в единице объема 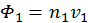 , а также самому телесному углу:
, а также самому телесному углу: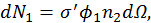
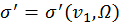 имеет размерность площади и в общем случае зависит от скорости сближения частиц, в нашей задаче это
имеет размерность площади и в общем случае зависит от скорости сближения частиц, в нашей задаче это  . Величина
. Величина 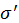 зависит от сорта частиц и характеризует конкретную природу их взаимодействия. Величина
зависит от сорта частиц и характеризует конкретную природу их взаимодействия. Величина 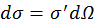 носит название дифференциального сечения рассеяния в элемент телесного угла
носит название дифференциального сечения рассеяния в элемент телесного угла 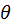 . Тогда полное число частиц, рассеянное в телесный угол 4π за 1 с в расчете на 1 м3, составит
. Тогда полное число частиц, рассеянное в телесный угол 4π за 1 с в расчете на 1 м3, составит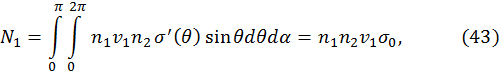
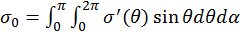 — полное сечение рассеяния. Величина
— полное сечение рассеяния. Величина 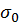 характеризует интегральный эффект, т. е. полное число частиц, покидающий поток за единицу времени в единице объема. Геометрическая интерпретация полного сечения — это площадь мишени, соответствующей одной частице типа 2. Численное значение сечения для электрически нейтральных частиц имеет порядок
характеризует интегральный эффект, т. е. полное число частиц, покидающий поток за единицу времени в единице объема. Геометрическая интерпретация полного сечения — это площадь мишени, соответствующей одной частице типа 2. Численное значение сечения для электрически нейтральных частиц имеет порядок  м2.
м2.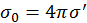 . Откуда
. Откуда 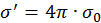 . Параметр
. Параметр 


