ХИМИЧЕСКИЙ ПОТЕНЦИАЛ И ИОНИЗАЦИОННОЕ РАВНОВЕСИЕ
В разделе 2.2 были определены условия равновесия двух систем, находящихся в тепловом и диффузном контакте. Эти условия сводятся к равенству температур и химических потенциалов контактирующих систем. Рассмотрим эти условия применительно к задаче об ионизационном равновесии. Известно, что при сильном свыше 5000 К нагревании газов молекулы практически полностью диссоциированы, а образовавшиеся атомы частично ионизованы. Наряду с ионами в газе при этом появляются освободившиеся в результате ионизации электроны. Механизмы ионизации при сильном нагревании газа связаны с различными столкновениями частиц, составляющих газ. При высоких температурах нагрева, когда кинетическая энергия частиц велика, такие столкновения могут привести к освобождению электронов с электронных оболочек атомов — ионизации. Следует отметить, что имеет место и обратный процесс — рекомбинация, когда ион, объединяясь с электроном, образует нейтральный атом. В равновесной ситуации при некоторой температуре устанавливается состояние с постоянным числом заряженных частиц в смеси, а скорости поступления заряженных частиц от ионизации и исчезновения их в результате рекомбинации равны. Таким образом, нагретый до высокой температуры газ по сути представляет собой смесь нейтрального газа, газа ионов и газа электронов. Рассмотрим равновесное состояние такой смеси. Итак, мы имеем три системы — нейтральный газ, газ ионов и газ электронов, находящиеся в равновесии друг с другом. Легко распространить условия равновесия двух систем на большее их число. В частности для трех систем имеем
где индексами Для того чтобы составить уравнение равновесия для химических потенциалов трех рассматриваемых систем, рассмотрим подробнее физический смысл химического потенциала. Выше при выводе распределения Гиббса для малого изменения энтропии некоторой системы мы получили следующее выражение
Переходя здесь к бесконечно малым приращениям и вспоминая определения температуры и химического потенциала, получим
При постоянном объеме, занимаемом системой, и при постоянной температуре она сохраняет равновесное состояние при изменении числа частиц в ней. Условием равновесия является, как было показано,
Из полученной формулы видно, что для указанных условий химический потенциал численно равен изменению энергии системы при изменении числа частиц в ней на одну. Составим уравнения равновесия, исходя из данного определения химического потенциала. Рассмотрим реакцию ионизации, когда из системы нейтралов исчезает одна частица, а одновременно в системах ионов и электронов пребывает по одной частице. Энергия системы нейтралов при этом изменится на величину
Чтобы использовать полученное уравнение для расчета степени ионизации, выведем формулу для химического потенциала идеального газа. Для этого сравним выражения для постоянной
Из получившегося уравнения найдем химический потенциал идеального газа
Используя найденное выражения для химического потенциала, приведем уравнение ионизационного равновесия виду
Здесь обозначено
С учетом того, что
Определим степень ионизации газа как отношение концентрации ионов
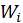 часто записывают в виде часто записывают в виде 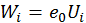 , ,  — потенциал ионизации. Если энергию ионизации выражать в электрон вольтах, то ее значение численно совпадает с потенциалом ионизации. Потенциал ионизации изменяется от нескольких вольт для легко ионизуемых паров металлов до примерно 20 В у инертных газов. Полученное уравнение носит имя индийского физика Саха и позволяет рассчитывать степень ионизации газа при заданной энергии ионизации, массе частицы и статистических весах атома и иона. Статистический вес электрона, как указывалось ранее, — потенциал ионизации. Если энергию ионизации выражать в электрон вольтах, то ее значение численно совпадает с потенциалом ионизации. Потенциал ионизации изменяется от нескольких вольт для легко ионизуемых паров металлов до примерно 20 В у инертных газов. Полученное уравнение носит имя индийского физика Саха и позволяет рассчитывать степень ионизации газа при заданной энергии ионизации, массе частицы и статистических весах атома и иона. Статистический вес электрона, как указывалось ранее, 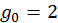 . Статистические веса атома и иона заметно выше, чем у электрона. Поэтому для упрощения расчетов часто полагают . Статистические веса атома и иона заметно выше, чем у электрона. Поэтому для упрощения расчетов часто полагают 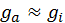 . При этом формула Саха несколько упрощается . При этом формула Саха несколько упрощается
В качестве примера на рис. 17 построена рассчитанная по последней формуле зависимость степени ионизации от температуры для паров железа (
|

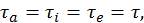
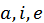 отмечены температуры соответственно нейтральных атомов, ионов и электронов.
отмечены температуры соответственно нейтральных атомов, ионов и электронов.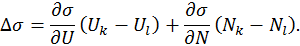
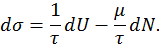
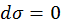 . Поэтому из последнего равенства найдем
. Поэтому из последнего равенства найдем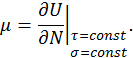
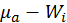 ; здесь мы учли не только определяемое химическим потенциалом «термодинамическое» изменение энергии
; здесь мы учли не только определяемое химическим потенциалом «термодинамическое» изменение энергии 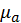 , но и потерю энергии связи электрона и ядра атома на величину энергии ионизации
, но и потерю энергии связи электрона и ядра атома на величину энергии ионизации 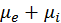 . Следуя закону сохранения энергии, нам осталось только приравнять описанные порции
. Следуя закону сохранения энергии, нам осталось только приравнять описанные порции
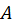 в общем случае распределения Гиббса, (37) с ее выражением для частного случая идеального газа (39)
в общем случае распределения Гиббса, (37) с ее выражением для частного случая идеального газа (39)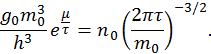
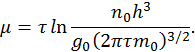
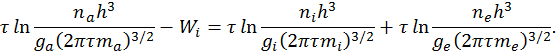
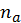 ,
, 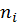 ,
, 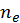 — концентрации,
— концентрации,  ,
,  ,
,  — число внутренних степеней вырождения (статистические веса),
— число внутренних степеней вырождения (статистические веса), 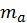 ,
, 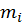 ,
,  — массы соответственно нейтральных частиц, ионов и электронов. Разделим уравнение на
— массы соответственно нейтральных частиц, ионов и электронов. Разделим уравнение на  и объединим логарифмические слагаемые. При этом получим
и объединим логарифмические слагаемые. При этом получим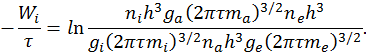
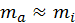 , последнее выражение можно преобразовать к виду
, последнее выражение можно преобразовать к виду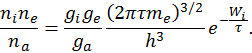
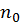 :
: 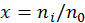 . Если предположить только однократную ионизацию атомов, то в этом случае, очевидно,
. Если предположить только однократную ионизацию атомов, то в этом случае, очевидно, 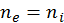 При этом имеем
При этом имеем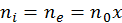 ,
,  . Подставляя эти соотношение в последнее уравнение и выражая энергетическую температуру
. Подставляя эти соотношение в последнее уравнение и выражая энергетическую температуру  , найдем
, найдем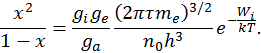
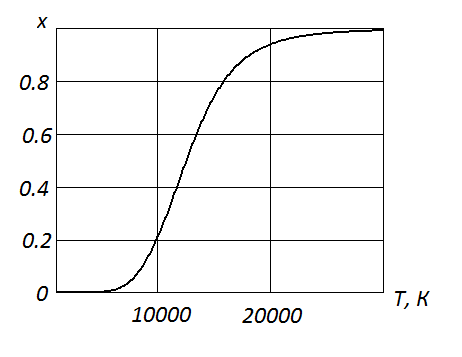 Рис. 17. Температурная зависимость степени ионизации для паров железа
Рис. 17. Температурная зависимость степени ионизации для паров железа
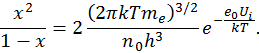
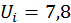 В) при концентрации
В) при концентрации 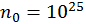 1/м3.
1/м3.


