ЧАСТОТА СТОЛКНОВЕНИЙ
Траектория частицы в газе представляет собой ломаную линию. Сумма длин всех отрезков ломаной линии, пройденной за 1 с, численно равна средней скорости частицы в газе
Рассмотрим более строгое определение частоты столкновений. В общем случае вычислить число рассеяний частиц типа 1 в малый телесный угол при учете движения частиц типа 1 со скоростью
Подсчитаем количество столкновений, происходящих в единице объема газа в единицу времени. Выделим в единице объема часть частиц первого сорта
Аналогично для частиц типа 2
Подсчитаем количество столкновений группы частиц типа 1
где
Используя стандартное определение средней величины
получим
Число столкновений, которое испытывает одна частица типа 1 с частицами типа 2 — частоту столкновений
Сравнивая с формулой для частоты столкновений (44), полученной в модели жестких сфер ( Приведенные выше общие понятия и выражения для сечения столкновения, частоты и длины свободного пробега могут быть обобщены на случай любых процессов парного взаимодействия — ядерные и химические реакции, ионизация, возбуждение и т. д. В этих случаях говорят, например, о сечении ядерной реакции, сечении ионизации и т. д. Если газ представляет собой смесь из K компонент, то рассчитать частоту столкновений частицы одного из типов, составляющих смесь, например, типа 1, можно просуммировав частоты столкновений выбранного типа частицы по отношению ко всем другим типам частиц смеси:
где Поскольку частота столкновений связана с длиной свободного пробега соотношением
где
|

 . Среднюю частоту столкновений — число столкновений, испытываемых частицей за 1 с, найдем, разделив путь пройденной частицей за 1 с на длину свободного пробега
. Среднюю частоту столкновений — число столкновений, испытываемых частицей за 1 с, найдем, разделив путь пройденной частицей за 1 с на длину свободного пробега
 и типа 2 — со скоростью
и типа 2 — со скоростью  можно по формуле
можно по формуле
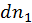 , у которых скорости лежат в интервале
, у которых скорости лежат в интервале  . Число частиц в единице объема, обладающих скоростью из указанного интервала, найдем с помощью функции распределения по скоростям
. Число частиц в единице объема, обладающих скоростью из указанного интервала, найдем с помощью функции распределения по скоростям



 . Вычислим число столкновений частиц типа 1 с частицами типа 2 в единице объема за единицу времени
. Вычислим число столкновений частиц типа 1 с частицами типа 2 в единице объема за единицу времени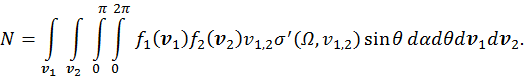


 — найдем из последней формулы
— найдем из последней формулы (45)
(45) ), видим, что (45) дает общую формулу, которая позволяет учесть зависимость сечения столкновения от скоростей частиц.
), видим, что (45) дает общую формулу, которая позволяет учесть зависимость сечения столкновения от скоростей частиц.
 — частота столкновений частиц типа 1 с частицами типа i.
— частота столкновений частиц типа 1 с частицами типа i. , то из формулы для частоты столкновений в смеси найдем
, то из формулы для частоты столкновений в смеси найдем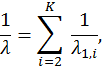
 — длина свободного пробега частицы типа 1 между ее столкновениями с частицей типа i.
— длина свободного пробега частицы типа 1 между ее столкновениями с частицей типа i.


