В газовой плазме электрического разряда наряду с нейтральными частицами появляются электрически заряженные — ионы и электроны. Сильно ионизованная горячая плазма полностью состоит из ионов и электронов. Выше мы рассматривали модели столкновений, например, модель жестких сфер, применимые к случаю ближнего взаимодействия, когда частицы взаимодействуют на расстоянии порядка размеров самих частиц. Взаимодействие заряженных частиц описывается в рамках закона Кулона. При этом расстояние, на котором частицы испытывают влияние друг друга, оказывается существенно большим. В этом случае мы имеем дело с так называемыми дальнодействующими силами взаимодействия.
В общем случае для расчета взаимодействия частиц необходимо знать начальные условия — скорости и взаимное положение частиц, массы сталкивающихся частиц и потенциал взаимодействия  , с помощью которого рассчитывается сила взаимодействия
, с помощью которого рассчитывается сила взаимодействия  , где
, где  — расстояние между частицами. Во всех практически важных случаях взаимодействия частиц сила взаимодействия частиц является центральной, т. е. зависит только от расстояния между частицами
— расстояние между частицами. Во всех практически важных случаях взаимодействия частиц сила взаимодействия частиц является центральной, т. е. зависит только от расстояния между частицами  . Примерами потенциалов взаимодействия являются:
. Примерами потенциалов взаимодействия являются:
·
 Рис. 21. Потенциал взаимодействия ионов в твердом теле
Рис. 21. Потенциал взаимодействия ионов в твердом теле
|
кулоновский потенциал
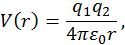
где  — заряды частиц;
— заряды частиц;
· потенциал взаимодействия разноименных ионов в ионном кристалле (рис. 21)
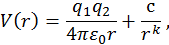
где  ,
, 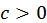 ,
,  .
.
· потенциал Леннарда–Джонса, используемый при оценке взаимодействия молекул
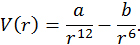
Основной целью анализа взаимодействия частиц является расчет угла рассеяния — угла отклонения траектории частицы после взаимодействия частиц. В данном разделе мы рассмотрим расчет угла рассеяния при взаимодействии заряженных частиц в соответствии с законом Кулона или, как говорят, рассеяния на кулоновском потенциале. Существует точное решение задачи о рассеянии в поле кулоновской силы. Здесь мы рассмотрим упрощенный подход.
Рассмотрим взаимодействие положительного иона с электроном, имеющим равный по модулю и противоположный по знаку заряд. Поскольку масса иона примерно на три порядка больше массы электрона, то ион можно считать покоящимся и анализировать движение электрона в поле неподвижного иона. Условия взаимодействия электрона с полем иона характеризуются прицельным параметром  и начальной скоростью
и начальной скоростью  (рис. 22). Предположим, что траектория электрона отклоняется от первоначального направления на угол
(рис. 22). Предположим, что траектория электрона отклоняется от первоначального направления на угол 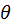 (рис. 22). При этом в силу закона сохранения энергии кинетическая энергия электрона
(рис. 22). При этом в силу закона сохранения энергии кинетическая энергия электрона  , где
, где  — скорость электрона до взаимодействия, сохраняет свое значение и после взаимодействия, поскольку по предположению ион, как тяжелая частица, покоится в течение всего процесса. Поэтому вектор скорости электрона меняет лишь свое направление, сохраняя абсолютную величину (рис. 22). Используем далее закон сохранения импульса
— скорость электрона до взаимодействия, сохраняет свое значение и после взаимодействия, поскольку по предположению ион, как тяжелая частица, покоится в течение всего процесса. Поэтому вектор скорости электрона меняет лишь свое направление, сохраняя абсолютную величину (рис. 22). Используем далее закон сохранения импульса
 Рис. 22. К расчету угла рассеяния электрона (
Рис. 22. К расчету угла рассеяния электрона ( ) при его взаимодействии с ионом ( ) при его взаимодействии с ионом ( ) )
|

Беря последнее уравнение по модулю, получим  . Длину вектора изменения скорости электрона
. Длину вектора изменения скорости электрона  легко найти, как длину основания равнобедренного треугольника с углом
легко найти, как длину основания равнобедренного треугольника с углом 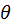 при вершине (рис. 22)
при вершине (рис. 22)  . Величина силы притяжения электрона ионом определяется законом Кулона. При этом расстояние между частицами в области взаимодействия (участок поворота траектории) примерно равно прицельному параметру
. Величина силы притяжения электрона ионом определяется законом Кулона. При этом расстояние между частицами в области взаимодействия (участок поворота траектории) примерно равно прицельному параметру  . Поэтому
. Поэтому  . Время взаимодействия
. Время взаимодействия  оценим по очевидной формуле
оценим по очевидной формуле  , которая следует из того, что наибольшее по траектории движения силовое воздействие на электрон достигается, когда последний находится на расстоянии максимального сближения с ионом, равном
, которая следует из того, что наибольшее по траектории движения силовое воздействие на электрон достигается, когда последний находится на расстоянии максимального сближения с ионом, равном  . Подставляя найденные параметры в уравнение закона сохранения импульса, получим
. Подставляя найденные параметры в уравнение закона сохранения импульса, получим

Отсюда
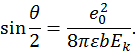
При малых углах рассеяния θ  . Поэтому
. Поэтому
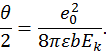
Полученный результат для малых углов рассеяния является частным случаем точного решения для произвольных углов, полученного Э. Резерфордом.
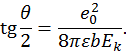
Рассмотрим более строгий вывод формулы Резерфорда, основанный на использовании системы координат, связанной с центром масс сталкивающихся частиц.
Силы воздействия частиц в газах является дальнодействующими, т. е. они проявляются на некотором расстоянии между частицами. Центральными называются силы, действующие между двумя частицами, направленные по линии, соединяющей частицы. Последние рассматриваются как материальные точки (рис. 23). На рис. 23 векторы r 1 и r 2 отмечают положение частиц 1 и 2 в пространстве. Вектор  направлен из точки 1 в точку 2:
направлен из точки 1 в точку 2:  ,
,  1 — сила, действующая на частицу 1,
1 — сила, действующая на частицу 1,  — сила, действующая на частицу 2.
— сила, действующая на частицу 2.
В соответствии с определением центральных сил
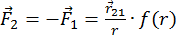 , где
, где  =
=  .
.
 Рис. 23. Траектория отталкивающихся частиц при кулоновском взаимодействии
Рис. 23. Траектория отталкивающихся частиц при кулоновском взаимодействии
|
Центральными являются силы взаимодействия двух точечных зарядов, двух точечных масс (гравитационное взаимодействие), тогда как взаимодействие двух диполей определяется не только расстоянием между ними, но и взаимной ориентацией диполей, так что в этом случае силы не являются центральными.
Обозначим  , где
, где  — потенциал силы. Рассмотрим изменение кинетической энергии Wk при движении частиц:
— потенциал силы. Рассмотрим изменение кинетической энергии Wk при движении частиц:

 .
.
Из последнего равенства следует, что:  , или
, или  . Эта формула показывает, что при движении в поле центральных сил остается постоянной сумма кинетической энергии обеих частиц и потенциальной энергии их взаимодействия. Следовательно, это взаимодействие — упругое, если у силы есть потенциал. Рассмотрим векторное произведение
. Эта формула показывает, что при движении в поле центральных сил остается постоянной сумма кинетической энергии обеих частиц и потенциальной энергии их взаимодействия. Следовательно, это взаимодействие — упругое, если у силы есть потенциал. Рассмотрим векторное произведение
 . (46)
. (46)
Первое слагаемое в правой части равно нулю, так как это есть векторное произведение двух параллельных векторов. Напишем выражение второго закона Ньютона применительно к движению каждой частицы:  ,
,  . Умножим первое уравнение на
. Умножим первое уравнение на  , а второе на
, а второе на  и сложим оба уравнения почленно
и сложим оба уравнения почленно  , или
, или 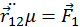 , где
, где  — приведенная масса. Из выражения для
— приведенная масса. Из выражения для  видно, что приведенная масса определяется в основном массой легкой частицы, если массы
видно, что приведенная масса определяется в основном массой легкой частицы, если массы  и
и  сильно различаются. Из последнего уравнения видно, что векторы:
сильно различаются. Из последнего уравнения видно, что векторы:  ,
,  и
и  параллельны, следовательно векторное произведение
параллельны, следовательно векторное произведение  . Таким образом из равенства (46) следует:
. Таким образом из равенства (46) следует:  или
или  , где
, где  — вектор с постоянным модулем и направлением. Поскольку векторное произведение есть вектор, перпендикулярный плоскости, в которой находятся векторы-сомножители, то из условия
— вектор с постоянным модулем и направлением. Поскольку векторное произведение есть вектор, перпендикулярный плоскости, в которой находятся векторы-сомножители, то из условия  следует, что
следует, что  и
и  лежат в плоскости, которая не меняет своей ориентации в пространстве. Таким образом, хотя траектории движения точек являются вообще говоря, пространственными кривыми, их относительное движение происходит в одной плоскости.
лежат в плоскости, которая не меняет своей ориентации в пространстве. Таким образом, хотя траектории движения точек являются вообще говоря, пространственными кривыми, их относительное движение происходит в одной плоскости.
Введем систему координат, связанную с центром масс. Радиус-вектор центра масс есть  .
.
Очевидно, что
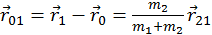 ;
;
 . (47)
. (47)
Из последних равенств видно, что векторы  и
и  направлены по одной прямой навстречу друг другу (антипараллельны) (рис. 23), причем
направлены по одной прямой навстречу друг другу (антипараллельны) (рис. 23), причем  и
и  . Дифференцируя по времени отношение для радиус-векторов, получим:
. Дифференцируя по времени отношение для радиус-векторов, получим:
 ,
,  ,
,
 .
.
Следовательно, скорости точек по отношению к центру масс антипараллельны.
Для описания движения в системе центра масс воспользуемся законами сохранения. В соответствии с законом сохранения импульса получим:
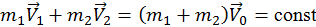 . (48)
. (48)
Из формулы (46) следует, что скорость движения центра масс  остается постоянной. Поскольку в системе центра масс частицы движутся в одной плоскости, и их скорости антипараллельны, может быть дана качественная картина их движения. Например, при отталкивании частиц траектории в системе центра масс имеют вид, подобный показанному на рис. 23.
остается постоянной. Поскольку в системе центра масс частицы движутся в одной плоскости, и их скорости антипараллельны, может быть дана качественная картина их движения. Например, при отталкивании частиц траектории в системе центра масс имеют вид, подобный показанному на рис. 23.
Рассчитаем кинетическую энергию в каждый момент времени:
 .
.
В последнем выражении  ,
,  — скорости в лабораторной системе координат. Выразим
— скорости в лабораторной системе координат. Выразим  и
и  через
через  ,
,  и
и  :
:
 ;
;  .
.
Домножим первое выражение на  , второе — на
, второе — на  и сложим результаты:
и сложим результаты:
 .
.
Из этого равенства следует, что кинетическая энергия в каждый момент времени может быть представлена как сумма кинетической энергии движения тела с массой  и скоростью центра масс и слагаемого, учитывающего относительное движение частиц. Выше было показано, что полная энергия взаимодействия двух частиц остается постоянной:
и скоростью центра масс и слагаемого, учитывающего относительное движение частиц. Выше было показано, что полная энергия взаимодействия двух частиц остается постоянной:  , следовательно,
, следовательно,
 . Но как было установлено выше, V0=const, поэтому
. Но как было установлено выше, V0=const, поэтому
 .
.
Если при  задана скорость относительно движения частиц.
задана скорость относительно движения частиц.  |r→ ∞ =V∞ , в силу того, что
|r→ ∞ =V∞ , в силу того, что  находим:
находим:
 .
.
Таким образом, первый интеграл движения имеет вид:
 .
.
Конкретная картина взаимодействия определяется выражением для потенциала  . Рассмотрим полярную систему координат, связанную с центром масс (рис. 23). В этой системе координат имеем:
. Рассмотрим полярную систему координат, связанную с центром масс (рис. 23). В этой системе координат имеем:
 ;
;  .
.
Справедливость последнего выражения вытекает из того факта, что  и
и  есть окружные скорости относительно центра масс (точки О). Таким образом, получаем:
есть окружные скорости относительно центра масс (точки О). Таким образом, получаем:  . В соответствии с законом сохранения энергии
. В соответствии с законом сохранения энергии
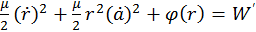 . (49)
. (49)
Можно написать еще один интеграл движения, выражающий закон сохранения момента количества движения:
 .
.
Здесь первый сомножитель в скобках — момент инерции, а второй окружная скорость. Как было показано  , следовательно:
, следовательно:
 |r→ ∞ .
|r→ ∞ .
В начальной стадии движения ( ),
),  , где
, где  — «прицельное расстояние», (рис. 23). Далее получаем
— «прицельное расстояние», (рис. 23). Далее получаем  но при
но при  ,
,  и, следовательно,
и, следовательно,  . Таким образом:
. Таким образом:
 |r→ ∞
|r→ ∞  .
.
Разделим почленно (п. 4) на 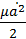
 .
.
Далее в последних членах заменим  на
на 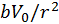
 (50а)
(50а)
Отсюда находим
 .
.
Запишем результат в более удобной для дальнейшего анализа форме
 (50б)
(50б)
Рассмотрим случай отталкивания частиц ( ). Это имеет место, например, при взаимодействии точечных электрических зарядов одного знака.
). Это имеет место, например, при взаимодействии точечных электрических зарядов одного знака.
Как следует из рис. 23, в начальной стадии  , т.к. с ростом a уменьшается. В соответствии с этим в формуле (49) следует взять знак «–». В конечной стадии взаимодействия
, т.к. с ростом a уменьшается. В соответствии с этим в формуле (49) следует взять знак «–». В конечной стадии взаимодействия  .
.
Качественный вид зависимости  показан на рис. 24. При изменении a от 0 до a 0 второе и третье слагаемые в подкоренном выражении уравнения (50б) будут расти по абсолютному значению. В момент, когда выполняется равенство
показан на рис. 24. При изменении a от 0 до a 0 второе и третье слагаемые в подкоренном выражении уравнения (50б) будут расти по абсолютному значению. В момент, когда выполняется равенство  , имеем
, имеем  . Этому моменту соответствует значение
. Этому моменту соответствует значение 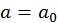 и
и  , где
, где  — наименьшее расстояние между частицами. Дальнейшее движение описывается правой восходящей частью кривой (рис. 24). Для этой части кривой в формуле (50) следует взять знак «+», а из симметрии кривой следует, что полное изменение угла во время столкновения
— наименьшее расстояние между частицами. Дальнейшее движение описывается правой восходящей частью кривой (рис. 24). Для этой части кривой в формуле (50) следует взять знак «+», а из симметрии кривой следует, что полное изменение угла во время столкновения  . Таким образом, при
. Таким образом, при  траектория частицы приходит из бесконечности и уходит на бесконечность, отклоняясь на угол
траектория частицы приходит из бесконечности и уходит на бесконечность, отклоняясь на угол  от первоначального направления. Движение, траектория которого есть кривая, приходящая из бесконечности и уходящая на бесконечность, называется инфинитным.
от первоначального направления. Движение, траектория которого есть кривая, приходящая из бесконечности и уходящая на бесконечность, называется инфинитным.
Рассмотрим случай, когда взаимодействующие частицы притягиваются. Движение и в этом случае будет инфинитным, если выражение  становится равным нулю. Если потенциал центральных сил задан в виде
становится равным нулю. Если потенциал центральных сил задан в виде  , то указанное условие может выполняться при
, то указанное условие может выполняться при  . Примером является кулоновское взаимодействие частиц с зарядами разных знаков (n =1). Возможен такой вид потенциала взаимодействия частиц
. Примером является кулоновское взаимодействие частиц с зарядами разных знаков (n =1). Возможен такой вид потенциала взаимодействия частиц  , когда знак подкоренного выражения остается положительным в течение всего процесса взаимодейст
, когда знак подкоренного выражения остается положительным в течение всего процесса взаимодейст
 а)
а)
 б)
Рис. 25. Потенциал взаимодействия пары ионов в твердом теле (а), Ван–дер–Ваальса (б) б)
Рис. 25. Потенциал взаимодействия пары ионов в твердом теле (а), Ван–дер–Ваальса (б)
|
вия частиц. В этом случае всегда

, и зависимость
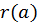
имеет вид кривой 2 (рис. 24), соответствующей случаю, когда частицы испытывают соударение. Все взаимодействия в поле центральных сил характеризуются потенциалом взаимодействия, определяемым конкретной физической природой этого процесса. Рассмотрим примеры.
1. Потенциал взаимодействия пары ионов в твердом теле (случай разноименно заряженных частиц) (рис. 25)
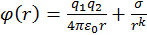 , (
, ( ,
,  ).
).
Точка  соответствует минимуму потенциала и следовательно состоянию равновесия. При
соответствует минимуму потенциала и следовательно состоянию равновесия. При  взаимодействие носит характер притяжения, при
взаимодействие носит характер притяжения, при  имеет место взаимное отталкивание частиц.
имеет место взаимное отталкивание частиц.
2. Потенциал Леннарда-Джонса используется как основная характеристика взаимодействия частиц в молекулярной физике ( ,
,  ):
):
 .
.
3. Потенциал Ван-дер Ваальса (рис. 25),  — соответствует точке равновесия. Величина
— соответствует точке равновесия. Величина  численно равна энергии связи молекулы.
численно равна энергии связи молекулы.
4. Кулоновское взаимодействие
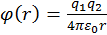 .
.
В этом случае, согласно (50б)

Положим  ;
;  . После замены переменных находим
. После замены переменных находим
 .
.
Табличный интеграл  , где
, где
 ,
,  .
.
При  подкоренное выражение в последнем интеграле обращается в нуль. Следовательно
подкоренное выражение в последнем интеграле обращается в нуль. Следовательно  , откуда
, откуда
 , и
, и  . Рассмотрим случай отталкивания частиц, т. е.
. Рассмотрим случай отталкивания частиц, т. е.  , тогда угол отклонения
, тогда угол отклонения
 . (51)
. (51)
В противоположном случае, когда  , имеем:
, имеем:
 . (52)
. (52)
Таким образом, в общем случае выражения (51) и (52) дают
 , или
, или  .
.
Последняя формула носит имя Резерфорда, она имеет большое значение при описании столкновений в плазме. Формулу Резерфорда можно записать в виде  , где
, где  . Параметр
. Параметр  есть значение прицельного расстояния, которому соответствует отклонение от первоначального направления на угол
есть значение прицельного расстояния, которому соответствует отклонение от первоначального направления на угол  .
.
Формулу Резерфорда чаще записывают в следующем виде

где 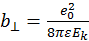 ,
,  ,
,  — скорость сближения взаимодействующих частиц,
— скорость сближения взаимодействующих частиц,  — приведенная масса,
— приведенная масса,  и
и  — массы сталкивающихся частиц. Согласно формуле Резерфорда, если значение прицельного параметра
— массы сталкивающихся частиц. Согласно формуле Резерфорда, если значение прицельного параметра 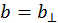 , то произойдет рассеяние на угол 900.
, то произойдет рассеяние на угол 900.

 , и зависимость
, и зависимость 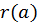 имеет вид кривой 2 (рис. 24), соответствующей случаю, когда частицы испытывают соударение. Все взаимодействия в поле центральных сил характеризуются потенциалом взаимодействия, определяемым конкретной физической природой этого процесса. Рассмотрим примеры.
имеет вид кривой 2 (рис. 24), соответствующей случаю, когда частицы испытывают соударение. Все взаимодействия в поле центральных сил характеризуются потенциалом взаимодействия, определяемым конкретной физической природой этого процесса. Рассмотрим примеры.

 , с помощью которого рассчитывается сила взаимодействия
, с помощью которого рассчитывается сила взаимодействия  , где
, где  — расстояние между частицами. Во всех практически важных случаях взаимодействия частиц сила взаимодействия частиц является центральной, т. е. зависит только от расстояния между частицами
— расстояние между частицами. Во всех практически важных случаях взаимодействия частиц сила взаимодействия частиц является центральной, т. е. зависит только от расстояния между частицами  Рис. 21. Потенциал взаимодействия ионов в твердом теле
Рис. 21. Потенциал взаимодействия ионов в твердом теле
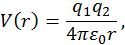
 — заряды частиц;
— заряды частиц;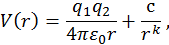
 ,
, 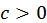 ,
,  .
.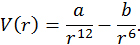
 и начальной скоростью
и начальной скоростью  (рис. 22). Предположим, что траектория электрона отклоняется от первоначального направления на угол
(рис. 22). Предположим, что траектория электрона отклоняется от первоначального направления на угол 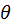 (рис. 22). При этом в силу закона сохранения энергии кинетическая энергия электрона
(рис. 22). При этом в силу закона сохранения энергии кинетическая энергия электрона  , где
, где  Рис. 22. К расчету угла рассеяния электрона (
Рис. 22. К расчету угла рассеяния электрона ( ) при его взаимодействии с ионом (
) при его взаимодействии с ионом ( )
)
 . Длину вектора изменения скорости электрона
. Длину вектора изменения скорости электрона  легко найти, как длину основания равнобедренного треугольника с углом
легко найти, как длину основания равнобедренного треугольника с углом  . Величина силы притяжения электрона ионом определяется законом Кулона. При этом расстояние между частицами в области взаимодействия (участок поворота траектории) примерно равно прицельному параметру
. Величина силы притяжения электрона ионом определяется законом Кулона. При этом расстояние между частицами в области взаимодействия (участок поворота траектории) примерно равно прицельному параметру  . Время взаимодействия
. Время взаимодействия  оценим по очевидной формуле
оценим по очевидной формуле  , которая следует из того, что наибольшее по траектории движения силовое воздействие на электрон достигается, когда последний находится на расстоянии максимального сближения с ионом, равном
, которая следует из того, что наибольшее по траектории движения силовое воздействие на электрон достигается, когда последний находится на расстоянии максимального сближения с ионом, равном 
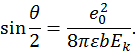
 . Поэтому
. Поэтому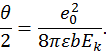
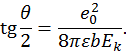
 направлен из точки 1 в точку 2:
направлен из точки 1 в точку 2:  ,
,  1 — сила, действующая на частицу 1,
1 — сила, действующая на частицу 1,  — сила, действующая на частицу 2.
— сила, действующая на частицу 2.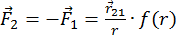 , где
, где  =
=  .
. Рис. 23. Траектория отталкивающихся частиц при кулоновском взаимодействии
Рис. 23. Траектория отталкивающихся частиц при кулоновском взаимодействии
 , где
, где  — потенциал силы. Рассмотрим изменение кинетической энергии Wk при движении частиц:
— потенциал силы. Рассмотрим изменение кинетической энергии Wk при движении частиц:
 .
. , или
, или  . Эта формула показывает, что при движении в поле центральных сил остается постоянной сумма кинетической энергии обеих частиц и потенциальной энергии их взаимодействия. Следовательно, это взаимодействие — упругое, если у силы есть потенциал. Рассмотрим векторное произведение
. Эта формула показывает, что при движении в поле центральных сил остается постоянной сумма кинетической энергии обеих частиц и потенциальной энергии их взаимодействия. Следовательно, это взаимодействие — упругое, если у силы есть потенциал. Рассмотрим векторное произведение . (46)
. (46) ,
,  . Умножим первое уравнение на
. Умножим первое уравнение на  , а второе на
, а второе на  и сложим оба уравнения почленно
и сложим оба уравнения почленно  , или
, или 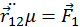 , где
, где  — приведенная масса. Из выражения для
— приведенная масса. Из выражения для  видно, что приведенная масса определяется в основном массой легкой частицы, если массы
видно, что приведенная масса определяется в основном массой легкой частицы, если массы  ,
,  и
и  параллельны, следовательно векторное произведение
параллельны, следовательно векторное произведение  . Таким образом из равенства (46) следует:
. Таким образом из равенства (46) следует:  или
или  , где
, где  — вектор с постоянным модулем и направлением. Поскольку векторное произведение есть вектор, перпендикулярный плоскости, в которой находятся векторы-сомножители, то из условия
— вектор с постоянным модулем и направлением. Поскольку векторное произведение есть вектор, перпендикулярный плоскости, в которой находятся векторы-сомножители, то из условия  следует, что
следует, что  лежат в плоскости, которая не меняет своей ориентации в пространстве. Таким образом, хотя траектории движения точек являются вообще говоря, пространственными кривыми, их относительное движение происходит в одной плоскости.
лежат в плоскости, которая не меняет своей ориентации в пространстве. Таким образом, хотя траектории движения точек являются вообще говоря, пространственными кривыми, их относительное движение происходит в одной плоскости. .
.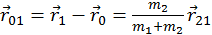 ;
; . (47)
. (47) и
и  направлены по одной прямой навстречу друг другу (антипараллельны) (рис. 23), причем
направлены по одной прямой навстречу друг другу (антипараллельны) (рис. 23), причем  и
и  . Дифференцируя по времени отношение для радиус-векторов, получим:
. Дифференцируя по времени отношение для радиус-векторов, получим: ,
,  ,
, .
.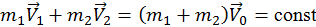 . (48)
. (48) остается постоянной. Поскольку в системе центра масс частицы движутся в одной плоскости, и их скорости антипараллельны, может быть дана качественная картина их движения. Например, при отталкивании частиц траектории в системе центра масс имеют вид, подобный показанному на рис. 23.
остается постоянной. Поскольку в системе центра масс частицы движутся в одной плоскости, и их скорости антипараллельны, может быть дана качественная картина их движения. Например, при отталкивании частиц траектории в системе центра масс имеют вид, подобный показанному на рис. 23. .
. ,
,  — скорости в лабораторной системе координат. Выразим
— скорости в лабораторной системе координат. Выразим  и
и  через
через  и
и  :
: ;
;  .
. , второе — на
, второе — на  и сложим результаты:
и сложим результаты: .
. и скоростью центра масс и слагаемого, учитывающего относительное движение частиц. Выше было показано, что полная энергия взаимодействия двух частиц остается постоянной:
и скоростью центра масс и слагаемого, учитывающего относительное движение частиц. Выше было показано, что полная энергия взаимодействия двух частиц остается постоянной:  , следовательно,
, следовательно,  . Но как было установлено выше, V0=const, поэтому
. Но как было установлено выше, V0=const, поэтому .
. задана скорость относительно движения частиц.
задана скорость относительно движения частиц.  |r→ ∞ =V∞ , в силу того, что
|r→ ∞ =V∞ , в силу того, что  находим:
находим: .
. .
. . Рассмотрим полярную систему координат, связанную с центром масс (рис. 23). В этой системе координат имеем:
. Рассмотрим полярную систему координат, связанную с центром масс (рис. 23). В этой системе координат имеем: ;
;  .
. и
и  есть окружные скорости относительно центра масс (точки О). Таким образом, получаем:
есть окружные скорости относительно центра масс (точки О). Таким образом, получаем:  . В соответствии с законом сохранения энергии
. В соответствии с законом сохранения энергии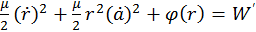 . (49)
. (49) .
. , следовательно:
, следовательно: |r→ ∞ .
|r→ ∞ . , где
, где  но при
но при  и, следовательно,
и, следовательно,  . Таким образом:
. Таким образом: |r→ ∞
|r→ ∞  .
.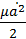
 .
. на
на 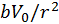
 (50а)
(50а) .
. (50б)
(50б) ). Это имеет место, например, при взаимодействии точечных электрических зарядов одного знака.
). Это имеет место, например, при взаимодействии точечных электрических зарядов одного знака. , т.к. с ростом a уменьшается. В соответствии с этим в формуле (49) следует взять знак «–». В конечной стадии взаимодействия
, т.к. с ростом a уменьшается. В соответствии с этим в формуле (49) следует взять знак «–». В конечной стадии взаимодействия  показан на рис. 24. При изменении a от 0 до a 0 второе и третье слагаемые в подкоренном выражении уравнения (50б) будут расти по абсолютному значению. В момент, когда выполняется равенство
показан на рис. 24. При изменении a от 0 до a 0 второе и третье слагаемые в подкоренном выражении уравнения (50б) будут расти по абсолютному значению. В момент, когда выполняется равенство  , имеем
, имеем  . Этому моменту соответствует значение
. Этому моменту соответствует значение 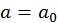 и
и  , где
, где  — наименьшее расстояние между частицами. Дальнейшее движение описывается правой восходящей частью кривой (рис. 24). Для этой части кривой в формуле (50) следует взять знак «+», а из симметрии кривой следует, что полное изменение угла во время столкновения
— наименьшее расстояние между частицами. Дальнейшее движение описывается правой восходящей частью кривой (рис. 24). Для этой части кривой в формуле (50) следует взять знак «+», а из симметрии кривой следует, что полное изменение угла во время столкновения  . Таким образом, при
. Таким образом, при  траектория частицы приходит из бесконечности и уходит на бесконечность, отклоняясь на угол
траектория частицы приходит из бесконечности и уходит на бесконечность, отклоняясь на угол  от первоначального направления. Движение, траектория которого есть кривая, приходящая из бесконечности и уходящая на бесконечность, называется инфинитным.
от первоначального направления. Движение, траектория которого есть кривая, приходящая из бесконечности и уходящая на бесконечность, называется инфинитным. становится равным нулю. Если потенциал центральных сил задан в виде
становится равным нулю. Если потенциал центральных сил задан в виде  , то указанное условие может выполняться при
, то указанное условие может выполняться при  . Примером является кулоновское взаимодействие частиц с зарядами разных знаков (n =1). Возможен такой вид потенциала взаимодействия частиц
. Примером является кулоновское взаимодействие частиц с зарядами разных знаков (n =1). Возможен такой вид потенциала взаимодействия частиц  а)
а)
 б)
Рис. 25. Потенциал взаимодействия пары ионов в твердом теле (а), Ван–дер–Ваальса (б)
б)
Рис. 25. Потенциал взаимодействия пары ионов в твердом теле (а), Ван–дер–Ваальса (б)
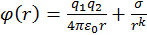 , (
, ( соответствует минимуму потенциала и следовательно состоянию равновесия. При
соответствует минимуму потенциала и следовательно состоянию равновесия. При  взаимодействие носит характер притяжения, при
взаимодействие носит характер притяжения, при  имеет место взаимное отталкивание частиц.
имеет место взаимное отталкивание частиц. ,
,  ):
): .
. численно равна энергии связи молекулы.
численно равна энергии связи молекулы.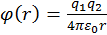 .
.
 ;
;  . После замены переменных находим
. После замены переменных находим .
. , где
, где ,
,  .
. подкоренное выражение в последнем интеграле обращается в нуль. Следовательно
подкоренное выражение в последнем интеграле обращается в нуль. Следовательно  , откуда
, откуда  , и
, и  . Рассмотрим случай отталкивания частиц, т. е.
. Рассмотрим случай отталкивания частиц, т. е.  , тогда угол отклонения
, тогда угол отклонения . (51)
. (51) . (52)
. (52) , или
, или  .
. , где
, где  . Параметр
. Параметр  есть значение прицельного расстояния, которому соответствует отклонение от первоначального направления на угол
есть значение прицельного расстояния, которому соответствует отклонение от первоначального направления на угол  .
.
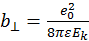 ,
,  ,
,  — скорость сближения взаимодействующих частиц,
— скорость сближения взаимодействующих частиц,  — приведенная масса,
— приведенная масса,  и
и  — массы сталкивающихся частиц. Согласно формуле Резерфорда, если значение прицельного параметра
— массы сталкивающихся частиц. Согласно формуле Резерфорда, если значение прицельного параметра 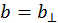 , то произойдет рассеяние на угол 900.
, то произойдет рассеяние на угол 900.


