ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ. РАСПРЕДЕЛЕНИЕ ГИББСА
 и числом частиц и числом частиц  . Природа энергии . Природа энергии  может быть различной. В частности для идеального газа это суммарная кинетическая энергия поступательного движения частиц, его составляющих. С точки зрения статистической термодинамики природа энергии может быть различной. В частности для идеального газа это суммарная кинетическая энергия поступательного движения частиц, его составляющих. С точки зрения статистической термодинамики природа энергии  не имеет принципиального значения. Степень вырождения значений пары параметров не имеет принципиального значения. Степень вырождения значений пары параметров  , ,  некоторой системы обозначим некоторой системы обозначим 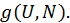
Рассмотрим две системы, находящиеся в тепловом контакте. При таком взаимодействии систем возможен обмен энергией, но не частицами. При этом предположим, что обмен энергией возможен только между системами, а от внешнего мира обе системы термодинамически изолированы (рис. 14). Обозначим параметры обеих систем соответственно
Подсчитаем степень вырождения для объединенной системы. На каждое фиксированное квантовое состояние системы 1 допустимы будет
По определению, равновесному состоянию объединенной системы будет соответствовать максимум
Из (31) легко найти, что
Сокращая на
Назовем энтропией натуральный логарифм полного числа разрешенных квантовых состояний системы
Тогда последнее равенство можно переписать в виде
Поскольку значения степени вырождения Дадим еще одно определение. Назовем энергетической температурой τ величину, определяемую с помощью равенства
Отсюда приходим к следующему условию равновесия двух систем в тепловом контакте
Иными словами при термодинамическом равновесии двух систем, находящихся в тепловом контакте, температуры систем равны друг другу. Предположим, что рассматриваемые нами две системы находятся не только в тепловом, но и диффузном контакте, т. е. системы обмениваются не только энергией, но и частицами, и
Теперь полный дифференциал степени вырождения объединенной системы будет выглядеть как
Поскольку при термодинамическом равновесии, как было показано выше,
Как и ранее из (31) последовало
Поскольку
и (33)
Первое равенство мы получили выше, из него последовало
При этом второе условие термодинамического равновесия (33) можно представить в виде
Таким образом, если две системы, пребывающие в тепловом и диффузном контакте друг с другом, находятся в термодинамическом равновесии, то равны их энергетические температуры и химические потенциалы Рассмотрим теперь тепловой и диффузный контакт двух систем, одна из которых значительно больше другой, так что число частиц в ней и ее энергия много больше, чем соответствующие характеристики второй системы. Первую (большую) систему назовем резервуаром, вторая (меньшая) сохраняет свое название. Рассмотрим тепловой и диффузный контакт системы и резервуара. При этом по-прежнему предполагаем их изоляцию от внешнего мира, так, что суммарное число части и энергия равны соответственно
Поэтому искомое отношение вероятностей есть
Здесь мы воспользовались определением энтропии
где
Выше мы установили, что
Возвращая полученное выражение в показатель экспоненты, получим
Вспоминая определение температуры
Экспонента, стоящая в числителе и знаменателе выражения для отношения вероятностей, носит название фактора Гиббса. Фактически последняя формула означает, что вероятность обнаружить систему с энергией
где Для систем с фиксированным числом частиц меняться может только их энергия. Соответствующая вероятность в этом случае пропорциональна фактору Больцмана
Для того чтобы найти константу пропорциональности воспользуемся свойством полной вероятности: сумма вероятностей всех возможных состояний системы равна единице, поскольку пребывание системы в одном из разрешенных квантовых состояний является достоверным событием. Таким образом, имеем
Отсюда
где в знаменателе фигурирует так называемая большая сумма или сумма Гиббса Аналогично для системы с фиксированным числом частиц найдем
где
|

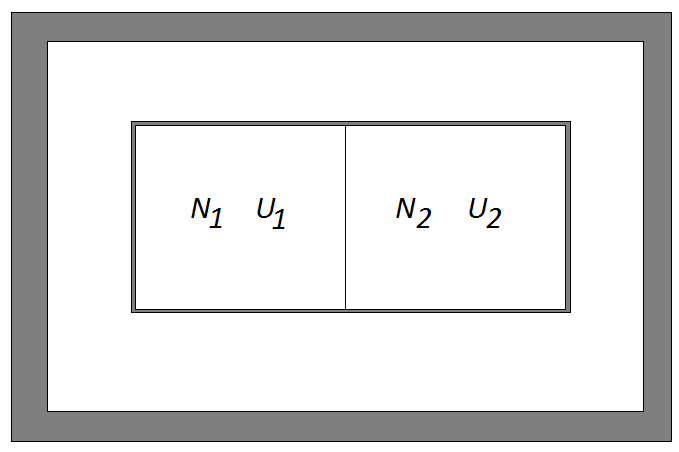 Рис. 14. Две системы в тепловом и диффузном контакте
Рис. 14. Две системы в тепловом и диффузном контакте
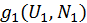 и
и 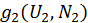 . При этом
. При этом  и
и  постоянны,
постоянны,  и
и 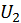 могут быть различны. Изолированность систем от внешнего мира означает, что суммарная энергия состоящих в тепловом контакте систем остается неизменной, т. е.
могут быть различны. Изолированность систем от внешнего мира означает, что суммарная энергия состоящих в тепловом контакте систем остается неизменной, т. е.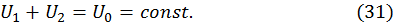
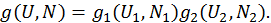
 . В точке максимума полный дифференциал
. В точке максимума полный дифференциал 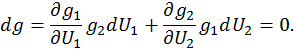
 . Поэтому разделив последнее выражение на
. Поэтому разделив последнее выражение на  , получим
, получим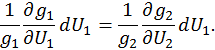
 , получим
, получим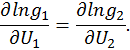
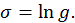

 могут быть очень велики, использование энтропии, как логарифма этой величины является более удобным.
могут быть очень велики, использование энтропии, как логарифма этой величины является более удобным.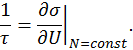


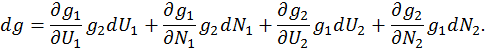
 , из последнего выражения имеем
, из последнего выражения имеем
 , так и из (32) имеем
, так и из (32) имеем 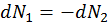 . Разделим последнее уравнение на
. Разделим последнее уравнение на 

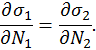
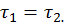 Определим химический потенциал μ с помощью соотношения
Определим химический потенциал μ с помощью соотношения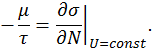

 ,
, 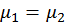 .
.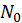 и
и 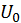 и неизменны. Поэтому если энергия и число частиц системы равны соответственно
и неизменны. Поэтому если энергия и число частиц системы равны соответственно  и
и 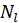 , где
, где 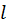 — номер некоторого энергетического уровня и числа частиц системы, то значения соответствующих параметров резервуара будут равны
— номер некоторого энергетического уровня и числа частиц системы, то значения соответствующих параметров резервуара будут равны 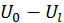 и
и 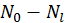 . Найдем отношение вероятности обнаружить систему в состоянии с энергией и числом частиц
. Найдем отношение вероятности обнаружить систему в состоянии с энергией и числом частиц  ,
, 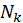 . Для подсчета этого отношения заметим, что число реализаций фиксированного состояния
. Для подсчета этого отношения заметим, что число реализаций фиксированного состояния  .
.
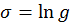 . Искомое отношение вероятностей можно переписать в виде
. Искомое отношение вероятностей можно переписать в виде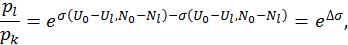
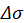 — разность энтропий резервуара при переходе системы из состояния
— разность энтропий резервуара при переходе системы из состояния  . Разложим выражение для
. Разложим выражение для  в ряд Тейлора вблизи точки
в ряд Тейлора вблизи точки 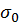 , характеризующей объединенную систему:
, характеризующей объединенную систему: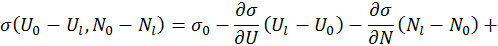

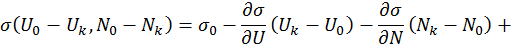
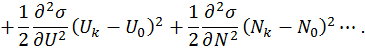
 поскольку система намного меньше резервуара. Поэтому в выписанных здесь разложениях в степенной ряд можно пренебречь различием
поскольку система намного меньше резервуара. Поэтому в выписанных здесь разложениях в степенной ряд можно пренебречь различием 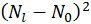 и
и 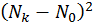 ,
, 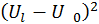 и
и 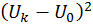 , а также в членах более высокого порядка. Поэтому составляя разность, получим
, а также в членах более высокого порядка. Поэтому составляя разность, получим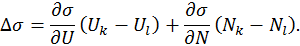
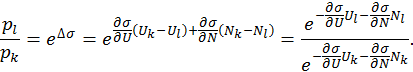
 и химического потенциала
и химического потенциала  , последнее выражение можно преобразовать к виду
, последнее выражение можно преобразовать к виду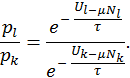
 и числом частиц
и числом частиц 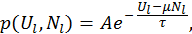
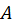 — коэффициент пропорциональности.
— коэффициент пропорциональности.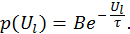
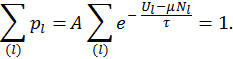
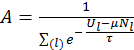 , а вероятность
, а вероятность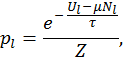
 .
.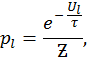
 — большая статистическая сумма Больцмана.
— большая статистическая сумма Больцмана.


