В данном разделе рассматривается применение теории, основанной на уравнении Шредингера к описанию движения электронов в кристаллических твердых телах.
 Рис. 11. Периодическая потенциальная функция
Рис. 11. Периодическая потенциальная функция
|
Особенностью строения кристаллических твердых тел является наличие структурированной решетки, т. е. такое положение ядер и атомов, которое может быть получено повторением (трансляцией) элементарной ячейки вдоль осей координатной системы. Потенциальная функция

в таких условиях становится периодической функцией координат, с чем мы не сталкивались в предыдущих разделах. Вместе с тем периодический потенциал самым существенным образом влияет на особенности движения и энергию электронов в твердом теле, что позволило установить решение уравнения Шредингера.
В качестве простейшей модельной задачи рассмотрим одномерное движение электрона вдоль оси x при условии, что потенциальный рельеф представляет собой последовательность прямоугольных потенциальных барьеров одинаковой высоты  и ширины
и ширины  , расположенных на равных расстояниях
, расположенных на равных расстояниях  . Таким образом, в данной задаче мы имеем дело с периодической потенциальной функцией, причем период функции
. Таким образом, в данной задаче мы имеем дело с периодической потенциальной функцией, причем период функции  (рис. 11). Вид одномерного стационарного уравнения Шредингера хорошо известен из предыдущих разделов
(рис. 11). Вид одномерного стационарного уравнения Шредингера хорошо известен из предыдущих разделов
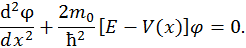
Потенциальную функцию в соответствии с рис. 11 мы можем определить следующим образом

где  — любое целое число (
— любое целое число (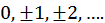 ). Решение уравнения Шредингера в виде функции Блоха
). Решение уравнения Шредингера в виде функции Блоха

где  — периодическая функция решетки, следовательно
— периодическая функция решетки, следовательно
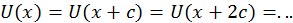
Найдем уравнение, которому должна удовлетворять функция  . Для этого подставим данное представление для
. Для этого подставим данное представление для  в уравнение Шредингера. При этом для областей между барьерами
в уравнение Шредингера. При этом для областей между барьерами

для областей внутри барьеров
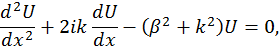
где  ,
, 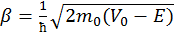 . Решения выписанных здесь уравнений есть соответственно
. Решения выписанных здесь уравнений есть соответственно
 ,
,  ,
,
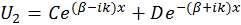 ,
,  .
.
Как обычно, для определения неизвестных постоянных 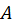 ,
, 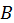 ,
, 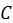 ,
,  применим условия сшивания на границах подобластей
применим условия сшивания на границах подобластей
 ,
, 
 ,
, 
Подставляя в эти условия выписанные решения, получим алгебраическую систему четырех линейных однородных уравнений, относительно 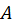 ,
, 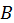 ,
, 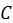 ,
,  :
:





Для существования нетривиального решения однородной системы необходимо равенство нулю ее главного определителя. Это приводит к уравнению

Полученное уравнение связывает между собой волновое число  и параметры
и параметры  и
и  , содержащие собственные значения энергии
, содержащие собственные значения энергии  . Решение данного уравнения весьма сложно. Поэтому мы упростим его, предполагая, что потенциальные барьеры имеют исчезающее малую ширину (приближение Кронига–Пенни). Пусть
. Решение данного уравнения весьма сложно. Поэтому мы упростим его, предполагая, что потенциальные барьеры имеют исчезающее малую ширину (приближение Кронига–Пенни). Пусть 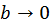 , а
, а  , но таким образом, чтобы произведение ширины барьера на высоту
, но таким образом, чтобы произведение ширины барьера на высоту  оставалось конечным. При этом
оставалось конечным. При этом 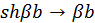 и
и 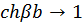 . Таким образом, последнее уравнение перепишется в виде
. Таким образом, последнее уравнение перепишется в виде
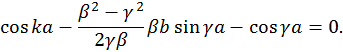
После преобразований последнее соотношение можно привести к виду
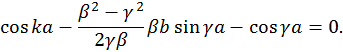
 Рис. 12. Образование разрешенных энергетических зон
Рис. 12. Образование разрешенных энергетических зон
|
С учетом того, что в рассматриваемом приближении
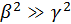
, можно положить

. Поэтому последнее равенство приводится к виду
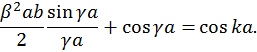
Обозначим эффективную площадь барьера при предельном переходе как

Окончательно придем к уравнению

На рис. 12 построена зависимость левой части уравнения от  . Поскольку правая часть уравнения (30) не может по модулю превосходить единицу, то решения существуют лишь в интервалах значений аргумента левой части
. Поскольку правая часть уравнения (30) не может по модулю превосходить единицу, то решения существуют лишь в интервалах значений аргумента левой части  , для которых левая часть уравнения меньше 1. На рис. 12 эти интервалы заштрихованы. Поскольку параметр
, для которых левая часть уравнения меньше 1. На рис. 12 эти интервалы заштрихованы. Поскольку параметр  однозначно связан с энергией электрона, то существование допустимых интервалов его изменения порождает допустимые интервалы изменения энергии, называемые энергетическими зонами. Качественно энергетический спектр электронов в твердом теле показан на рис. 13. Главная черта энергетического спектра электронов в твердом теле — чередование разрешенных и запрещенных интервалов (зон) изменения энергии. Ширина разрешенных зон зависит от параметра P, характеризующего прозрачность потенциальных барьеров. Поэтому с уменьшение P ширина допустимых интервалов на рис. 12, а, следовательно, и ширина разрешенных энергетических зон возрастает. Рассмотрим два предельных случая, когда
однозначно связан с энергией электрона, то существование допустимых интервалов его изменения порождает допустимые интервалы изменения энергии, называемые энергетическими зонами. Качественно энергетический спектр электронов в твердом теле показан на рис. 13. Главная черта энергетического спектра электронов в твердом теле — чередование разрешенных и запрещенных интервалов (зон) изменения энергии. Ширина разрешенных зон зависит от параметра P, характеризующего прозрачность потенциальных барьеров. Поэтому с уменьшение P ширина допустимых интервалов на рис. 12, а, следовательно, и ширина разрешенных энергетических зон возрастает. Рассмотрим два предельных случая, когда  и
и 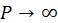 . В первом случае барьеры становятся полностью прозрачными. При
. В первом случае барьеры становятся полностью прозрачными. При  из (30) получаем
из (30) получаем  или
или  , Подставляя сюда выражение для
, Подставляя сюда выражение для  , получим
, получим

где  импульс электрона. Последняя формула соответствует свободному движению электрона, она была получена нами в разделе 1.2. Во втором предельном случае
импульс электрона. Последняя формула соответствует свободному движению электрона, она была получена нами в разделе 1.2. Во втором предельном случае 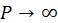 имеем полностью непрозрачные барьеры. При этом из (30) следует
имеем полностью непрозрачные барьеры. При этом из (30) следует  , т. е.
, т. е.  ,
,  , откуда
, откуда
 ,
,
что в точности совпадает с решением для электрона, «запертого» в потенциальной яме, полученным нами ранее. Итак, в случае сильной связи  энергия электрона квантуется внутри разрешенной зоны. Можно показать, что это свойство имеет место, и в общем случае
энергия электрона квантуется внутри разрешенной зоны. Можно показать, что это свойство имеет место, и в общем случае  , однако в отличие от упомянутой потенциальной ямы с бесконечно высокими стенками число энергетических уровней в разрешенной зоне конечно и равно N. Таким образом, мы приходим к выводу о том, что энергетический спектр электронов в твердом теле (кристалле) представляет собой чередование разрешенных и запрещенных зон. При этом внутри разрешенных зон спектр энергий является дискретным.
, однако в отличие от упомянутой потенциальной ямы с бесконечно высокими стенками число энергетических уровней в разрешенной зоне конечно и равно N. Таким образом, мы приходим к выводу о том, что энергетический спектр электронов в твердом теле (кристалле) представляет собой чередование разрешенных и запрещенных зон. При этом внутри разрешенных зон спектр энергий является дискретным.

|
| Рис. 13. Схема заполнения энергетических зон электронов в твердом теле
|
 в таких условиях становится периодической функцией координат, с чем мы не сталкивались в предыдущих разделах. Вместе с тем периодический потенциал самым существенным образом влияет на особенности движения и энергию электронов в твердом теле, что позволило установить решение уравнения Шредингера.
в таких условиях становится периодической функцией координат, с чем мы не сталкивались в предыдущих разделах. Вместе с тем периодический потенциал самым существенным образом влияет на особенности движения и энергию электронов в твердом теле, что позволило установить решение уравнения Шредингера.
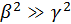 , можно положить
, можно положить  . Поэтому последнее равенство приводится к виду
. Поэтому последнее равенство приводится к виду

 Рис. 11. Периодическая потенциальная функция
Рис. 11. Периодическая потенциальная функция
 и ширины
и ширины  , расположенных на равных расстояниях
, расположенных на равных расстояниях  . Таким образом, в данной задаче мы имеем дело с периодической потенциальной функцией, причем период функции
. Таким образом, в данной задаче мы имеем дело с периодической потенциальной функцией, причем период функции  (рис. 11). Вид одномерного стационарного уравнения Шредингера хорошо известен из предыдущих разделов
(рис. 11). Вид одномерного стационарного уравнения Шредингера хорошо известен из предыдущих разделов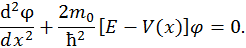

 — любое целое число (
— любое целое число (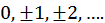 ). Решение уравнения Шредингера в виде функции Блоха
). Решение уравнения Шредингера в виде функции Блоха
 — периодическая функция решетки, следовательно
— периодическая функция решетки, следовательно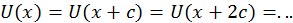
 в уравнение Шредингера. При этом для областей между барьерами
в уравнение Шредингера. При этом для областей между барьерами
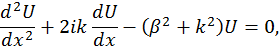
 ,
, 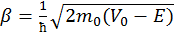 . Решения выписанных здесь уравнений есть соответственно
. Решения выписанных здесь уравнений есть соответственно ,
,  ,
,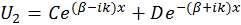 ,
,  .
.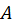 ,
, 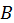 ,
, 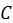 ,
,  применим условия сшивания на границах подобластей
применим условия сшивания на границах подобластей ,
, 
 ,
, 






 и параметры
и параметры  и
и  , содержащие собственные значения энергии
, содержащие собственные значения энергии  . Решение данного уравнения весьма сложно. Поэтому мы упростим его, предполагая, что потенциальные барьеры имеют исчезающее малую ширину (приближение Кронига–Пенни). Пусть
. Решение данного уравнения весьма сложно. Поэтому мы упростим его, предполагая, что потенциальные барьеры имеют исчезающее малую ширину (приближение Кронига–Пенни). Пусть 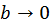 , а
, а  , но таким образом, чтобы произведение ширины барьера на высоту
, но таким образом, чтобы произведение ширины барьера на высоту  оставалось конечным. При этом
оставалось конечным. При этом 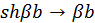 и
и 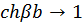 . Таким образом, последнее уравнение перепишется в виде
. Таким образом, последнее уравнение перепишется в виде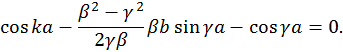
 Рис. 12. Образование разрешенных энергетических зон
Рис. 12. Образование разрешенных энергетических зон
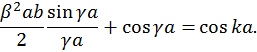


 . Поскольку правая часть уравнения (30) не может по модулю превосходить единицу, то решения существуют лишь в интервалах значений аргумента левой части
. Поскольку правая часть уравнения (30) не может по модулю превосходить единицу, то решения существуют лишь в интервалах значений аргумента левой части  однозначно связан с энергией электрона, то существование допустимых интервалов его изменения порождает допустимые интервалы изменения энергии, называемые энергетическими зонами. Качественно энергетический спектр электронов в твердом теле показан на рис. 13. Главная черта энергетического спектра электронов в твердом теле — чередование разрешенных и запрещенных интервалов (зон) изменения энергии. Ширина разрешенных зон зависит от параметра P, характеризующего прозрачность потенциальных барьеров. Поэтому с уменьшение P ширина допустимых интервалов на рис. 12, а, следовательно, и ширина разрешенных энергетических зон возрастает. Рассмотрим два предельных случая, когда
однозначно связан с энергией электрона, то существование допустимых интервалов его изменения порождает допустимые интервалы изменения энергии, называемые энергетическими зонами. Качественно энергетический спектр электронов в твердом теле показан на рис. 13. Главная черта энергетического спектра электронов в твердом теле — чередование разрешенных и запрещенных интервалов (зон) изменения энергии. Ширина разрешенных зон зависит от параметра P, характеризующего прозрачность потенциальных барьеров. Поэтому с уменьшение P ширина допустимых интервалов на рис. 12, а, следовательно, и ширина разрешенных энергетических зон возрастает. Рассмотрим два предельных случая, когда  и
и 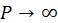 . В первом случае барьеры становятся полностью прозрачными. При
. В первом случае барьеры становятся полностью прозрачными. При  из (30) получаем
из (30) получаем  или
или  , Подставляя сюда выражение для
, Подставляя сюда выражение для 
 импульс электрона. Последняя формула соответствует свободному движению электрона, она была получена нами в разделе 1.2. Во втором предельном случае
импульс электрона. Последняя формула соответствует свободному движению электрона, она была получена нами в разделе 1.2. Во втором предельном случае  , т. е.
, т. е.  ,
,  , откуда
, откуда ,
, энергия электрона квантуется внутри разрешенной зоны. Можно показать, что это свойство имеет место, и в общем случае
энергия электрона квантуется внутри разрешенной зоны. Можно показать, что это свойство имеет место, и в общем случае  , однако в отличие от упомянутой потенциальной ямы с бесконечно высокими стенками число энергетических уровней в разрешенной зоне конечно и равно N. Таким образом, мы приходим к выводу о том, что энергетический спектр электронов в твердом теле (кристалле) представляет собой чередование разрешенных и запрещенных зон. При этом внутри разрешенных зон спектр энергий является дискретным.
, однако в отличие от упомянутой потенциальной ямы с бесконечно высокими стенками число энергетических уровней в разрешенной зоне конечно и равно N. Таким образом, мы приходим к выводу о том, что энергетический спектр электронов в твердом теле (кристалле) представляет собой чередование разрешенных и запрещенных зон. При этом внутри разрешенных зон спектр энергий является дискретным.



