| l
| m
| |L|
| Lz
| Y(α, θ)
|
|
|
|
|
| 
|
|
|
| 
| ħ
| 
|
|
| 
|
| 
|
| -1
| 
| -ħ
| 
|
Постоянная 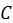 определяется из условия нормировки, которое при фиксированном удалении частицы от начала координат (жесткий ротатор) будет иметь вид
определяется из условия нормировки, которое при фиксированном удалении частицы от начала координат (жесткий ротатор) будет иметь вид

где  — элемент сферической поверхности единичного радиуса.
— элемент сферической поверхности единичного радиуса.
Физически данное условие означает обнаружение частицы где-либо на поверхности ротатора как достоверное событие. В частности для комбинации квантовых чисел  и
и  , когда
, когда  . Условие нормировки дает
. Условие нормировки дает

откуда  .
.
Отметим также, что плотность вероятности  для всех решений имеет вид
для всех решений имеет вид  и не зависит от азимутального угла
и не зависит от азимутального угла  . Поэтому произведение
. Поэтому произведение  есть вероятность обнаружить частицу между углами
есть вероятность обнаружить частицу между углами 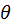 и
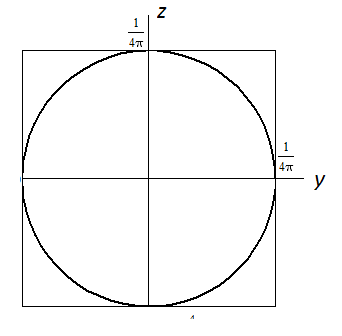
и  . Графически распределения плотности вероятности для волновых функции
. Графически распределения плотности вероятности для волновых функции  , приведенных в табл. 1, построены на рис. 9.
, приведенных в табл. 1, построены на рис. 9.
| 
| 
|

| 
| 
|
| Рис. 9. Распределение плотности вероятности для ротатора
|
Чтобы получить полную картину, график нужно вращать вокруг оси  . При этом в случае комбинации квантовых чисел
. При этом в случае комбинации квантовых чисел  ,
,  , называемой -состоянием, направление вращения, направление момента импульса не зависит от угла
, называемой -состоянием, направление вращения, направление момента импульса не зависит от угла 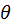 , что очевидно, объясняется тем, что в этом состоянии
, что очевидно, объясняется тем, что в этом состоянии  . Покоящаяся материальная точка может с равной вероятностью находится на поверхности сферы. В случае -состояния с
. Покоящаяся материальная точка может с равной вероятностью находится на поверхности сферы. В случае -состояния с 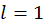 ,
,  , наиболее вероятной из всех траекторий ротатора является та, которая расположена в плоскости
, наиболее вероятной из всех траекторий ротатора является та, которая расположена в плоскости  . При этом состояния с
. При этом состояния с  и
и  отличаются направлением вращения. В первом случае ротатор обладает правым вращением, когда
отличаются направлением вращения. В первом случае ротатор обладает правым вращением, когда  направлен в положительном направлении оси
направлен в положительном направлении оси  . Левому вращению (
. Левому вращению ( ) соответствует обратное направление вектора L. Наконец, в p -состоянии c
) соответствует обратное направление вектора L. Наконец, в p -состоянии c 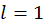 и
и  наиболее вероятной является орбита, проходящая через ось
наиболее вероятной является орбита, проходящая через ось  . При этом момент импульса перпендикулярен оси
. При этом момент импульса перпендикулярен оси  .
.
Обратимся теперь к уравнению для радиальной состaвляющей волновой функции  (23). Рассмотрим простейшее решение радиального уравнения, которое имеет место при
(23). Рассмотрим простейшее решение радиального уравнения, которое имеет место при  . Выполняя дифференцирование в первом слагаемом левой части и подставляя выражение для
. Выполняя дифференцирование в первом слагаемом левой части и подставляя выражение для  , получим
, получим

где  ,
,  . Будем искать простейшее решение, ограниченное при
. Будем искать простейшее решение, ограниченное при  и стремящееся к нулю при
и стремящееся к нулю при  в виде
в виде  . После подстановки этого представления в последнее уравнение и сокращения на
. После подстановки этого представления в последнее уравнение и сокращения на  , получим
, получим

Перегруппировав слагаемые, получим

Последнее равенство должно выполняться тождественно при любых изменениях  , но поскольку первое слагаемое в круглых скобках является константой данное требование можно выполнить только в случае, если одновременно
, но поскольку первое слагаемое в круглых скобках является константой данное требование можно выполнить только в случае, если одновременно  и
и  . Отсюда получаем
. Отсюда получаем


откуда  . Полученные для 1s состояния (
. Полученные для 1s состояния ( ) результаты являются частным случаем общего решения уравнения (23), которое приводит к следующей формуле для энергии электрона
) результаты являются частным случаем общего решения уравнения (23), которое приводит к следующей формуле для энергии электрона

где  носит название главного квантового числа и принимает любые положительные целые значения,
носит название главного квантового числа и принимает любые положительные целые значения,  — радиальное квантовое число. Величина, обратная к
— радиальное квантовое число. Величина, обратная к  , является боровским радиусом
, является боровским радиусом

При этом радиальная волновая функция R для 1s состояния ( ) будет записана в виде
) будет записана в виде  . Поскольку в этом состоянии угловая составляющая волновой функции является константой, то полное решение для данной комбинации квантовых чисел получит вид
. Поскольку в этом состоянии угловая составляющая волновой функции является константой, то полное решение для данной комбинации квантовых чисел получит вид

где индексы у φ есть соответственно значения главного, орбитального и магнитного квантового числа, 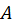 — постоянная, которую следует искать с помощью условия нормировки
— постоянная, которую следует искать с помощью условия нормировки

В переменных сферической системы координат последнее условие получает вид

Также достаточно простым по форме выглядит решение для  состояния (
состояния ( )
)

С помощью формулы (27) можно построить схему энергетических уровней атома водорода (рис. 10). Для этого ее удобно представить в виде

где  эВ. Электрон в связанном состоянии имеет отрицательную энергию, т. е. находится в потенциальной яме, верхний уровень стенок которой соответствует нулевой энергии. По мере роста главного квантового числа электрон приближается к свободному состоянию, для которого характерно
эВ. Электрон в связанном состоянии имеет отрицательную энергию, т. е. находится в потенциальной яме, верхний уровень стенок которой соответствует нулевой энергии. По мере роста главного квантового числа электрон приближается к свободному состоянию, для которого характерно  . Из рис. 10 видно, что для того, чтобы перевести электрон в свободное состояние — «извлечь из потенциальной ямы» — необходимо затратить энергию
. Из рис. 10 видно, что для того, чтобы перевести электрон в свободное состояние — «извлечь из потенциальной ямы» — необходимо затратить энергию  эВ. В результате атом лишается электрона и становится положительно заряженным ионом. Этот акт называется ионизацией, а приведенное значение энергии — энергией ионизации.
эВ. В результате атом лишается электрона и становится положительно заряженным ионом. Этот акт называется ионизацией, а приведенное значение энергии — энергией ионизации.

|
| Рис. 10. Схема энергетических уровней атома водорода
|
Характерно, что в связанном состоянии значение энергии электрона приобретает дискретный набор значений, образуя, так называемый дискретный энергетический спектр. Аналогичное поведение энергетического спектра мы наблюдали в задаче об одномерной потенциальной яме. В свободном состоянии электрон обладает сплошным спектром, т. е. может принимать любое значение энергии.
Из рис. 10 также видно, что одно и тоже значение энергии электрона, начиная со второго уровня, реализуется в различных комбинациях квантовых чисел. Явление, когда разрешенное значение энергии квантовой системы достигается при нескольких разрешенных комбинациях квантовых чисел, называется вырождением энергетического уровня, а число таких комбинаций — степенью вырождения. Из рис. 10 видно, что чем выше главное квантовое число, тем выше степень вырождения соответствующего уровня. Отметим также, что рис. 10 не дает полного представления о степени вырождения энергетических уровней электрона в атоме водорода, поскольку там не показаны варианты реализации уровней энергии с различными значениями магнитного квантового числа m, а также не учтены два различных значения спина электрона в каждом состоянии. Учет этих факторов дает выражение для степени вырождения энергетического уровня электрона в атоме водорода  .
.






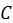 определяется из условия нормировки, которое при фиксированном удалении частицы от начала координат (жесткий ротатор) будет иметь вид
определяется из условия нормировки, которое при фиксированном удалении частицы от начала координат (жесткий ротатор) будет иметь вид
 — элемент сферической поверхности единичного радиуса.
— элемент сферической поверхности единичного радиуса. и
и  , когда
, когда  . Условие нормировки дает
. Условие нормировки дает
 .
. для всех решений имеет вид
для всех решений имеет вид  и не зависит от азимутального угла
и не зависит от азимутального угла  . Поэтому произведение
. Поэтому произведение  есть вероятность обнаружить частицу между углами
есть вероятность обнаружить частицу между углами 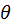 и
и  . Графически распределения плотности вероятности для волновых функции
. Графически распределения плотности вероятности для волновых функции  , приведенных в табл. 1, построены на рис. 9.
, приведенных в табл. 1, построены на рис. 9.





 . При этом в случае комбинации квантовых чисел
. При этом в случае комбинации квантовых чисел  . Покоящаяся материальная точка может с равной вероятностью находится на поверхности сферы. В случае -состояния с
. Покоящаяся материальная точка может с равной вероятностью находится на поверхности сферы. В случае -состояния с 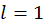 ,
,  , наиболее вероятной из всех траекторий ротатора является та, которая расположена в плоскости
, наиболее вероятной из всех траекторий ротатора является та, которая расположена в плоскости  . При этом состояния с
. При этом состояния с  и
и  отличаются направлением вращения. В первом случае ротатор обладает правым вращением, когда
отличаются направлением вращения. В первом случае ротатор обладает правым вращением, когда  направлен в положительном направлении оси
направлен в положительном направлении оси  (23). Рассмотрим простейшее решение радиального уравнения, которое имеет место при
(23). Рассмотрим простейшее решение радиального уравнения, которое имеет место при  . Выполняя дифференцирование в первом слагаемом левой части и подставляя выражение для
. Выполняя дифференцирование в первом слагаемом левой части и подставляя выражение для  , получим
, получим
 ,
,  . Будем искать простейшее решение, ограниченное при
. Будем искать простейшее решение, ограниченное при  и стремящееся к нулю при
и стремящееся к нулю при  в виде
в виде  . После подстановки этого представления в последнее уравнение и сокращения на
. После подстановки этого представления в последнее уравнение и сокращения на  , получим
, получим

 , но поскольку первое слагаемое в круглых скобках является константой данное требование можно выполнить только в случае, если одновременно
, но поскольку первое слагаемое в круглых скобках является константой данное требование можно выполнить только в случае, если одновременно  и
и  . Отсюда получаем
. Отсюда получаем

 . Полученные для 1s состояния (
. Полученные для 1s состояния (
 носит название главного квантового числа и принимает любые положительные целые значения,
носит название главного квантового числа и принимает любые положительные целые значения,  — радиальное квантовое число. Величина, обратная к
— радиальное квантовое число. Величина, обратная к  , является боровским радиусом
, является боровским радиусом
 ) будет записана в виде
) будет записана в виде  . Поскольку в этом состоянии угловая составляющая волновой функции является константой, то полное решение для данной комбинации квантовых чисел получит вид
. Поскольку в этом состоянии угловая составляющая волновой функции является константой, то полное решение для данной комбинации квантовых чисел получит вид
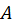 — постоянная, которую следует искать с помощью условия нормировки
— постоянная, которую следует искать с помощью условия нормировки

 состояния (
состояния ( )
)

 эВ. Электрон в связанном состоянии имеет отрицательную энергию, т. е. находится в потенциальной яме, верхний уровень стенок которой соответствует нулевой энергии. По мере роста главного квантового числа электрон приближается к свободному состоянию, для которого характерно
эВ. Электрон в связанном состоянии имеет отрицательную энергию, т. е. находится в потенциальной яме, верхний уровень стенок которой соответствует нулевой энергии. По мере роста главного квантового числа электрон приближается к свободному состоянию, для которого характерно  . Из рис. 10 видно, что для того, чтобы перевести электрон в свободное состояние — «извлечь из потенциальной ямы» — необходимо затратить энергию
. Из рис. 10 видно, что для того, чтобы перевести электрон в свободное состояние — «извлечь из потенциальной ямы» — необходимо затратить энергию 
 .
.


