Выше были рассмотрены модельные задачи, в которых потенциальная функция имеет простейший рельеф — ступень и прямоугольник. Реальные потенциальные функции, формирующиеся, в частности, в микроструктуре жидкостей и твердых тел, могут отличаться более сложной формой.
Получим приближенное выражение для коэффициента прозрачности барьера, заданного произвольной гладкой функцией  , как, например, на рис. 6. Для вывода формулы будем использовать вероятностную трактовку коэффициента прозрачности
, как, например, на рис. 6. Для вывода формулы будем использовать вероятностную трактовку коэффициента прозрачности  , как вероятности прохождения частицы сквозь барьер. Ограничим область анализа отрезком
, как вероятности прохождения частицы сквозь барьер. Ограничим область анализа отрезком  , в пределах которого энергия частицы ниже энергии барьера
, в пределах которого энергия частицы ниже энергии барьера  (рис. 6). Заменим далее в указанном отрезке потенциальную функцию
(рис. 6). Заменим далее в указанном отрезке потенциальную функцию 
 расположенными последовательно прямоугольными потенциальными барьерами равной ширины
расположенными последовательно прямоугольными потенциальными барьерами равной ширины  , высота которых соответствует текущему значению
, высота которых соответствует текущему значению  (рис. 6). Таким образом, задача оценки вероятности прохождения частицей исходного барьера
(рис. 6). Таким образом, задача оценки вероятности прохождения частицей исходного барьера  сводится к расчету вероятности прохождения частицей N прямоугольных потенциальных барьеров разной высоты. Поэтому следует вычислить вероятность одновременного выполнения N событий, каждое из которых является прохождением частицы через прямоугольный потенциальный барьер заданной амплитуды. Из теории вероятности известно, что вероятность одновременного выполнения N событий есть произведение вероятности отдельного события. Поэтому коэффициент прозрачности совокупности прямоугольных потенциальных барьеров вычислим как произведение коэффициентов прозрачности каждого из N прямоугольных барьеров, аппроксимирующих реальный барьер
сводится к расчету вероятности прохождения частицей N прямоугольных потенциальных барьеров разной высоты. Поэтому следует вычислить вероятность одновременного выполнения N событий, каждое из которых является прохождением частицы через прямоугольный потенциальный барьер заданной амплитуды. Из теории вероятности известно, что вероятность одновременного выполнения N событий есть произведение вероятности отдельного события. Поэтому коэффициент прозрачности совокупности прямоугольных потенциальных барьеров вычислим как произведение коэффициентов прозрачности каждого из N прямоугольных барьеров, аппроксимирующих реальный барьер
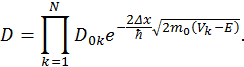
Поскольку коэффициенты  по порядку величины равны 1 для оценочных расчетов положим
по порядку величины равны 1 для оценочных расчетов положим  . Произведение экспонент, очевидно, преобразуется в одну экспоненциальную функцию с показателем, равным сумме показателей экспонент сомножителей в исходном выражении. Поэтому
. Произведение экспонент, очевидно, преобразуется в одну экспоненциальную функцию с показателем, равным сумме показателей экспонент сомножителей в исходном выражении. Поэтому

Устремляя в последнем выражении  , получим соответственно
, получим соответственно  . При этом сумма в показателе экспоненты последнего выражения переходит в интеграл
. При этом сумма в показателе экспоненты последнего выражения переходит в интеграл

Значения пределов интегрирования в (21) определяются, как точки пересечения потенциальной функции  с горизонтальной линией, соответствующей энергии частицы
с горизонтальной линией, соответствующей энергии частицы  (рис. 6).
(рис. 6).
В качестве примера вычислим коэффициент прозрачности потенциального барьера, на границе металлического тела при воздействии внешнего электрического поля. В обычных условиях на границе металл-вакуум имеет место потенциальный барьер ступенчатой формы, полностью препятствующий электронам покидать металл  (рис. 7). Разницу высоты барьера и энергии частицы принято называть работой выхода
(рис. 7). Разницу высоты барьера и энергии частицы принято называть работой выхода  . Преодоление данного барьера возможно, если дополнительно сообщить электронам энергию, превосходящую работу выхода. Это возможно при нагревании металла. В этом случае возникает термоэлектронная эмиссия.
. Преодоление данного барьера возможно, если дополнительно сообщить электронам энергию, превосходящую работу выхода. Это возможно при нагревании металла. В этом случае возникает термоэлектронная эмиссия.
 Рис. 7. К расчету коэффициента прозрачности потенциального барьера на границе металл–вакуум
Рис. 7. К расчету коэффициента прозрачности потенциального барьера на границе металл–вакуум
|
Другая возможность освобождения электронов с поверхности металла заключается в искажении формы потенциального барьера таким образом, чтобы его коэффициент прозрачности стал отличным от нуля. Такая ситуация возникает при приложении соответствующим образом направленного внешнего электрического поля

. В этом случае на электрон будет действовать сила
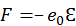
, а потенциал этой силы соответственно равен

. Нетрудно видеть, что при таком определении

. Поэтому совокупная потенциальная функция будет иметь не ступенчатую высотой

форму, а треугольную, описываемую формулой

(рис. 7). Для расчета коэффициента прозрачности такого барьера с помощью формулы (21) необходимо определить начало и конец отрезка интегрирования. Если начальная точка очевидно

, то конечная определяется из условия равенства энергии электрона
E энергии барьера:

Откуда 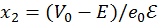 . Таким образом, имеем для коэффициента прозрачности
. Таким образом, имеем для коэффициента прозрачности

После интегрирования найдем
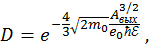
где  .
.
Таким образом, приложение внешнего электрического поля вследствие появления вероятности прохождения потенциального барьера на границе металл-вакуум ( ) приводит к выходу электронов из металла и соответствующему возникновению электрического тока. Данное явление носит название автоэлектронной или холодной эмиссии. Плотность тока автоэлектронной эмиссии пропорциональна коэффициенту прозрачности
) приводит к выходу электронов из металла и соответствующему возникновению электрического тока. Данное явление носит название автоэлектронной или холодной эмиссии. Плотность тока автоэлектронной эмиссии пропорциональна коэффициенту прозрачности  , где
, где  .
.
 . В этом случае на электрон будет действовать сила
. В этом случае на электрон будет действовать сила 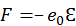 , а потенциал этой силы соответственно равен
, а потенциал этой силы соответственно равен  . Нетрудно видеть, что при таком определении
. Нетрудно видеть, что при таком определении  . Поэтому совокупная потенциальная функция будет иметь не ступенчатую высотой
. Поэтому совокупная потенциальная функция будет иметь не ступенчатую высотой  форму, а треугольную, описываемую формулой
форму, а треугольную, описываемую формулой  (рис. 7). Для расчета коэффициента прозрачности такого барьера с помощью формулы (21) необходимо определить начало и конец отрезка интегрирования. Если начальная точка очевидно
(рис. 7). Для расчета коэффициента прозрачности такого барьера с помощью формулы (21) необходимо определить начало и конец отрезка интегрирования. Если начальная точка очевидно  , то конечная определяется из условия равенства энергии электрона E энергии барьера:
, то конечная определяется из условия равенства энергии электрона E энергии барьера:

 , как, например, на рис. 6. Для вывода формулы будем использовать вероятностную трактовку коэффициента прозрачности
, как, например, на рис. 6. Для вывода формулы будем использовать вероятностную трактовку коэффициента прозрачности  , как вероятности прохождения частицы сквозь барьер. Ограничим область анализа отрезком
, как вероятности прохождения частицы сквозь барьер. Ограничим область анализа отрезком  , в пределах которого энергия частицы ниже энергии барьера
, в пределах которого энергия частицы ниже энергии барьера  (рис. 6). Заменим далее в указанном отрезке потенциальную функцию
(рис. 6). Заменим далее в указанном отрезке потенциальную функцию  расположенными последовательно прямоугольными потенциальными барьерами равной ширины
расположенными последовательно прямоугольными потенциальными барьерами равной ширины  , высота которых соответствует текущему значению
, высота которых соответствует текущему значению 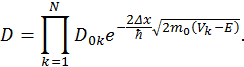
 по порядку величины равны 1 для оценочных расчетов положим
по порядку величины равны 1 для оценочных расчетов положим  . Произведение экспонент, очевидно, преобразуется в одну экспоненциальную функцию с показателем, равным сумме показателей экспонент сомножителей в исходном выражении. Поэтому
. Произведение экспонент, очевидно, преобразуется в одну экспоненциальную функцию с показателем, равным сумме показателей экспонент сомножителей в исходном выражении. Поэтому
 , получим соответственно
, получим соответственно  . При этом сумма в показателе экспоненты последнего выражения переходит в интеграл
. При этом сумма в показателе экспоненты последнего выражения переходит в интеграл
 (рис. 6).
(рис. 6). (рис. 7). Разницу высоты барьера и энергии частицы принято называть работой выхода
(рис. 7). Разницу высоты барьера и энергии частицы принято называть работой выхода  . Преодоление данного барьера возможно, если дополнительно сообщить электронам энергию, превосходящую работу выхода. Это возможно при нагревании металла. В этом случае возникает термоэлектронная эмиссия.
. Преодоление данного барьера возможно, если дополнительно сообщить электронам энергию, превосходящую работу выхода. Это возможно при нагревании металла. В этом случае возникает термоэлектронная эмиссия. Рис. 7. К расчету коэффициента прозрачности потенциального барьера на границе металл–вакуум
Рис. 7. К расчету коэффициента прозрачности потенциального барьера на границе металл–вакуум

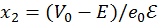 . Таким образом, имеем для коэффициента прозрачности
. Таким образом, имеем для коэффициента прозрачности
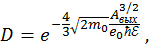
 ) приводит к выходу электронов из металла и соответствующему возникновению электрического тока. Данное явление носит название автоэлектронной или холодной эмиссии. Плотность тока автоэлектронной эмиссии пропорциональна коэффициенту прозрачности
) приводит к выходу электронов из металла и соответствующему возникновению электрического тока. Данное явление носит название автоэлектронной или холодной эмиссии. Плотность тока автоэлектронной эмиссии пропорциональна коэффициенту прозрачности  , где
, где  .
.


