Для того чтобы найти подходящий способ описание движения частиц при учете их волновых свойств, рассмотрим некоторые следствия электродинамической теории волн. Хорошо известно, что плоская монохроматическая волна описывается выражением:
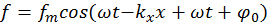 ,
,
где  — амплитуда,
— амплитуда, 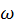 — круговая частота,
— круговая частота,  — волновое число (пространственный аналог круговой частоты),
— волновое число (пространственный аналог круговой частоты), 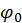 — начальная фаза. Положение постоянной фазы соответствует постоянному значению аргумента под знаком
— начальная фаза. Положение постоянной фазы соответствует постоянному значению аргумента под знаком 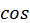 :
: 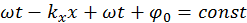 . Дифференцируя последнее выражение по времени, найдем скорость распространения фиксированной фазы — фазовую скорость
. Дифференцируя последнее выражение по времени, найдем скорость распространения фиксированной фазы — фазовую скорость 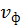 :
: 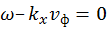 . Откуда
. Откуда 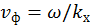 . В общем случае трехмерного движения выражение, описывающее волну, имеет вид
. В общем случае трехмерного движения выражение, описывающее волну, имеет вид 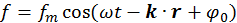 , где r — радиус вектор положения точки наблюдения волны, k — волновой вектор. Приведенные формулы для описания одномерной и пространственной волны не вполне удобны для применения по отношению к частицам, поскольку не позволяют указывать пространственное положение частиц. Иными словами данные выражения описывают волну, которая существует вдоль всей оси x или во всем пространстве, в то время как при длине волны Де-Бройля, меньшей размера области движения частиц, следует характеризовать координатами их положения в пространстве. Поэтому приведенные выражения для волны нуждаются в модификации.
, где r — радиус вектор положения точки наблюдения волны, k — волновой вектор. Приведенные формулы для описания одномерной и пространственной волны не вполне удобны для применения по отношению к частицам, поскольку не позволяют указывать пространственное положение частиц. Иными словами данные выражения описывают волну, которая существует вдоль всей оси x или во всем пространстве, в то время как при длине волны Де-Бройля, меньшей размера области движения частиц, следует характеризовать координатами их положения в пространстве. Поэтому приведенные выражения для волны нуждаются в модификации.
Для описания движения волн-частиц используются понятия волнового пакета. Волновой пакет представляет собой суперпозицию непрерывного спектра волн, затухающих по мере удаления от основной частоты ω 0 и основного волнового вектора k 0. Таким образом, волновой пакет для случая одномерного движения можно записать в виде интеграла
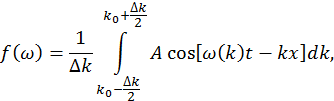
где без ограничения общности результата мы положили начальную фазу равной нулю. Функцию 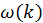 , выражающую связь между частотой и волновым вектором (дисперсионное соотношение), разложим в ряд Тейлора вблизи точки
, выражающую связь между частотой и волновым вектором (дисперсионное соотношение), разложим в ряд Тейлора вблизи точки 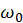 , ограничиваясь линейным приближением
, ограничиваясь линейным приближением 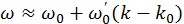 . После подстановки этой аппроксимации в предыдущее выражение и интегрирования найдем
. После подстановки этой аппроксимации в предыдущее выражение и интегрирования найдем
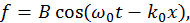
где 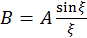 ,
, 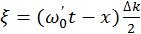 .
.
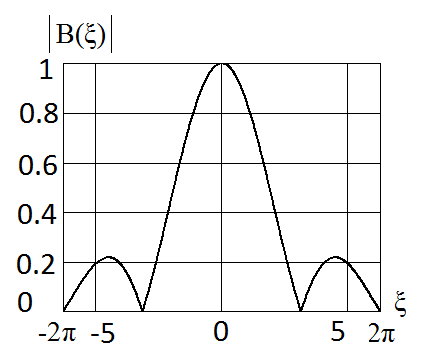 Рис. 1. Распределение интенсивности волнового пакета
Рис. 1. Распределение интенсивности волнового пакета
|
Найдем групповую скорость, т. е. скорость движения центра волнового пакета, которую можно отождествить со скоростью движения частицы. Таким образом групповая скорость это скорость движения точки, для которой
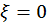
:
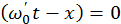
, откуда
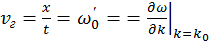
. На рис. 1 построен график функции

. Из рисунка видно, что амплитуда волн уменьшается примерно на порядок при смещении от центра пакета
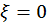
на расстояние
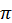
по оси

. Поэтому границы волнового пакета будут определяться условием
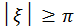
. Таким образом, измерение или расчет характеристик движения волны-частицы возможен только для пространственной области, размеры которой удовлетворяют неравенству
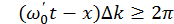
. Откуда при
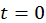
имеем условие
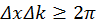
. Из ранее веденных соотношений для длины волны Де-Бройля
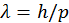
, где

— импульс частицы, и соотношения между длиной волны
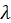
и волновым числом
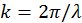
получаем
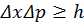 . (1)
. (1)
Неравенство (1) носит название соотношения неопределенностей Гейзенберга, физический смысл которого состоит в невозможности сколь угодно точного одновременного определения положения и импульса частицы. Например, при уменьшении 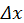 , что будет соответствовать повышению точности определения координаты, согласно (1) будет возрастать ошибка в определении импульса
, что будет соответствовать повышению точности определения координаты, согласно (1) будет возрастать ошибка в определении импульса 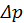 . Соотношение неопределенностей (1) обобщается и на пространственный случай, для чего его применяют для двух оставшихся декартовых координат
. Соотношение неопределенностей (1) обобщается и на пространственный случай, для чего его применяют для двух оставшихся декартовых координат 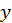 и
и  :
: 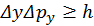 ,
, 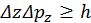 .
.
Если теперь в ранее выведенном неравенстве 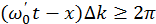 положить
положить  , то принимая за начало отсчета во времени
, то принимая за начало отсчета во времени 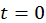 , получим неравенство вида
, получим неравенство вида 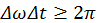 . Используя ранее введенную формулу Планка для энергии излучения
. Используя ранее введенную формулу Планка для энергии излучения 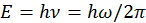 , последнее неравенство преобразуем к виду
, последнее неравенство преобразуем к виду
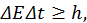 (2)
(2)
физический смысл которого состоит в том, что повышение точности измерения энергии частицы требует увеличения времени измерения. Иными словами исчерпывающая точность измерения энергии 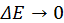 требует неограниченно длительного наблюдения
требует неограниченно длительного наблюдения 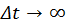 . Неравенство (2) получило название четвертого соотношения неопределенностей.
. Неравенство (2) получило название четвертого соотношения неопределенностей.
Факт существования соотношения неопределенностей и наличие максимума у функции, описывающей волновой пакет в точке локализации частицы, позволяет интерпретировать волны Де-Бройля, как волны некоторой функции, квадрат которой (это будет показано в следующем разделе) характеризует вероятность обнаружить частицу в заданном месте. Данная функция носит название волновой и обычно записывается в комплексном виде:
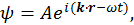 (3)
(3)
где  — мнимая единица. Данная интерпретация волновой функции полностью соответствует экспериментальным дифракционным картинам. Например, данная функция описывает области наибольшего почернения, образующиеся при облучении фотопластинок пучками электронов, проходящих через бериллиевую фольгу.
— мнимая единица. Данная интерпретация волновой функции полностью соответствует экспериментальным дифракционным картинам. Например, данная функция описывает области наибольшего почернения, образующиеся при облучении фотопластинок пучками электронов, проходящих через бериллиевую фольгу.
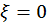 :
: 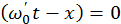 , откуда
, откуда 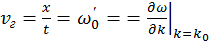 . На рис. 1 построен график функции
. На рис. 1 построен график функции  . Из рисунка видно, что амплитуда волн уменьшается примерно на порядок при смещении от центра пакета
. Из рисунка видно, что амплитуда волн уменьшается примерно на порядок при смещении от центра пакета 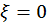 на расстояние
на расстояние 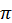 по оси
по оси  . Поэтому границы волнового пакета будут определяться условием
. Поэтому границы волнового пакета будут определяться условием 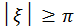 . Таким образом, измерение или расчет характеристик движения волны-частицы возможен только для пространственной области, размеры которой удовлетворяют неравенству
. Таким образом, измерение или расчет характеристик движения волны-частицы возможен только для пространственной области, размеры которой удовлетворяют неравенству 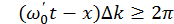 . Откуда при
. Откуда при 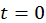 имеем условие
имеем условие 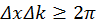 . Из ранее веденных соотношений для длины волны Де-Бройля
. Из ранее веденных соотношений для длины волны Де-Бройля 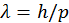 , где
, где  — импульс частицы, и соотношения между длиной волны
— импульс частицы, и соотношения между длиной волны 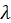 и волновым числом
и волновым числом 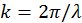 получаем
получаем

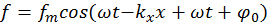 ,
, — амплитуда,
— амплитуда, 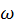 — круговая частота,
— круговая частота,  — волновое число (пространственный аналог круговой частоты),
— волновое число (пространственный аналог круговой частоты), 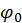 — начальная фаза. Положение постоянной фазы соответствует постоянному значению аргумента под знаком
— начальная фаза. Положение постоянной фазы соответствует постоянному значению аргумента под знаком 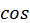 :
: 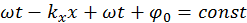 . Дифференцируя последнее выражение по времени, найдем скорость распространения фиксированной фазы — фазовую скорость
. Дифференцируя последнее выражение по времени, найдем скорость распространения фиксированной фазы — фазовую скорость 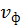 :
: 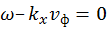 . Откуда
. Откуда 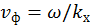 . В общем случае трехмерного движения выражение, описывающее волну, имеет вид
. В общем случае трехмерного движения выражение, описывающее волну, имеет вид 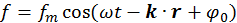 , где r — радиус вектор положения точки наблюдения волны, k — волновой вектор. Приведенные формулы для описания одномерной и пространственной волны не вполне удобны для применения по отношению к частицам, поскольку не позволяют указывать пространственное положение частиц. Иными словами данные выражения описывают волну, которая существует вдоль всей оси x или во всем пространстве, в то время как при длине волны Де-Бройля, меньшей размера области движения частиц, следует характеризовать координатами их положения в пространстве. Поэтому приведенные выражения для волны нуждаются в модификации.
, где r — радиус вектор положения точки наблюдения волны, k — волновой вектор. Приведенные формулы для описания одномерной и пространственной волны не вполне удобны для применения по отношению к частицам, поскольку не позволяют указывать пространственное положение частиц. Иными словами данные выражения описывают волну, которая существует вдоль всей оси x или во всем пространстве, в то время как при длине волны Де-Бройля, меньшей размера области движения частиц, следует характеризовать координатами их положения в пространстве. Поэтому приведенные выражения для волны нуждаются в модификации.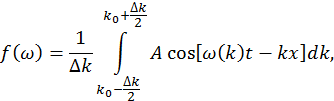
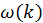 , выражающую связь между частотой и волновым вектором (дисперсионное соотношение), разложим в ряд Тейлора вблизи точки
, выражающую связь между частотой и волновым вектором (дисперсионное соотношение), разложим в ряд Тейлора вблизи точки 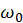 , ограничиваясь линейным приближением
, ограничиваясь линейным приближением 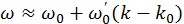 . После подстановки этой аппроксимации в предыдущее выражение и интегрирования найдем
. После подстановки этой аппроксимации в предыдущее выражение и интегрирования найдем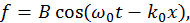
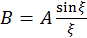 ,
, 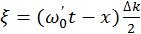 .
. Рис. 1. Распределение интенсивности волнового пакета
Рис. 1. Распределение интенсивности волнового пакета
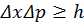 . (1)
. (1)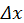 , что будет соответствовать повышению точности определения координаты, согласно (1) будет возрастать ошибка в определении импульса
, что будет соответствовать повышению точности определения координаты, согласно (1) будет возрастать ошибка в определении импульса 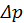 . Соотношение неопределенностей (1) обобщается и на пространственный случай, для чего его применяют для двух оставшихся декартовых координат
. Соотношение неопределенностей (1) обобщается и на пространственный случай, для чего его применяют для двух оставшихся декартовых координат 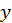 и
и  :
: 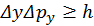 ,
, 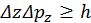 .
.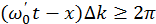 положить
положить  , то принимая за начало отсчета во времени
, то принимая за начало отсчета во времени 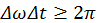 . Используя ранее введенную формулу Планка для энергии излучения
. Используя ранее введенную формулу Планка для энергии излучения 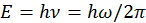 , последнее неравенство преобразуем к виду
, последнее неравенство преобразуем к виду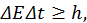 (2)
(2)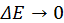 требует неограниченно длительного наблюдения
требует неограниченно длительного наблюдения 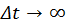 . Неравенство (2) получило название четвертого соотношения неопределенностей.
. Неравенство (2) получило название четвертого соотношения неопределенностей.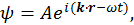 (3)
(3) — мнимая единица. Данная интерпретация волновой функции полностью соответствует экспериментальным дифракционным картинам. Например, данная функция описывает области наибольшего почернения, образующиеся при облучении фотопластинок пучками электронов, проходящих через бериллиевую фольгу.
— мнимая единица. Данная интерпретация волновой функции полностью соответствует экспериментальным дифракционным картинам. Например, данная функция описывает области наибольшего почернения, образующиеся при облучении фотопластинок пучками электронов, проходящих через бериллиевую фольгу.


