УРАВНЕНИЕ ШРЕДИНГЕРА
Из предыдущего раздела следует, что все частицы могут в зависимости от внешних пространственных и временных условий могут проявлять, как обычные, описываемые в рамках уравнений классической механики, так и волновые свойства, когда область пространственной локализации волнового пакета частицы или длина ee волны соизмеримы с размерами области движения. Очевидно, для описания движения частиц с учетом отмеченных свойств необходимы иные модели, которые охватывали бы, как классические, так и волновые свойства частиц. Базовым элементом такой модели явилось уравнение Шредингера. При этом в отличие от классической механики при математическом описании движения частиц используются не сами числовые характеристики движения (координата, импульс, энергия), а их операторы. Оператором будем называть некоторое действие, производимое над функцией. Такими действиями, например, являются дифференцирование или умножение на константу. Необходимость использования операторов в теории Шредингера возникает, в связи с тем, что искомой во всех расчетах является не имеющая физической размерности волновая функция (3). Рассмотрим вначале хорошо известное из курса теоретической механики уравнение
где
где Уравнение Шредингера выглядит похожим на классическое (4)
Здесь вместо полной энергии E и функции Гамильтона H фигурируют оператор энергии
и оператор Гамильтона
где
где
где
Существует строгое доказательство того, что уравнение Шредингера (5) преобразуется в уравнения классической механики в случае, если область локализации волнового пакета частицы значительно меньше размеров области движения. Здесь мы продемонстрируем этот переход для случая свободного движения частицы, когда
Используя формулу Планка
Уравнение Шредингера при одномерном движении и
После подстановки в него волновой функции (6) получим
Иными словами при свободном движении частицы, последняя обладает только кинетической энергией. Следует обратить внимание, что полученное выражение уже не содержит волновой функции. Вместе с тем до сих пор вопрос о физическом смысле волновой функции
комплексно сопряженное ему уравнение
где
Умножив последнее уравнение на заряд электрона e0, его можно привести к виду
где
Подставляя под знак интеграла выражение для объемной плотности заряда
Соотношение (10) называется условием нормировки волновой функции. Таким образом, волновая функция, найденная в результате решения дифференциального уравнения Шредингера, должна удовлетворять еще и условию нормировки (10). Обратимся к физическому смыслу условия нормировки. Выше мы отмечали, что положение электрона внутри объема
Поскольку функция
В частном случае одномерного движения частицы вдоль оси
Выше отмечалось, что в уравнении Шредингера в отличие от классических уравнений механики фигурируют не сами физические величины, характеризующие движение (энергия, импульс и т. д.), а их операторы. Поэтому для вычисления средних значений физических величин также используются операторы. Пусть физическая величина характеризуется оператором
Важно отметить, что для правильного применения последней формулы следует вначале аналитически определить результат действия оператора Волновая функция ψ как видно из уравнения Шредингера, в общем случае является комплексной функцией. В то же время средние значения наблюдаемых физических величин являются всегда числами действительными. Само по себе выражение (12) не гарантирует того, что вычисленный результат будет действительным числом. Поэтому определeнные требования предъявляются к операторам Приведем еще несколько важных свойств и понятий, относящихся к операторам квантовой механики. Операторы квантовой механики являются линейными. Математически это свойство выражается следующими формулами
где Собственными функциями
где Пусть функция
Таким образом, если оператор имеет лишь одно собственное число и одну собственную функцию, то это собственное значение будет совпадать с его средним значением. В случае, если оператор
Данное разложение аналогично разложению в ряд Фурье. Возможность и единственность такого разложения обеспечивается свойством полноты системы функций
Как отмечено выше, волновая функция частицы должна удовлетворять условию нормировки (10), применительно к разложению (13) это условие будет иметь вид
Если перемножить суммы под знаком интеграла и почленно проинтегрировать, то по свойству ортогональности системы функций
Последнее равенство позволяет трактовать величины
Последнее равенство еще раз подтверждает вероятностную трактовку коэффициентов
|

 , (4)
, (4) — энергия,
— энергия,  — функция Гамильтона. Если рассматривать движение уединенной частицы — материальной точки массой
— функция Гамильтона. Если рассматривать движение уединенной частицы — материальной точки массой  — в классической модели механики, то функция Гамильтона будет иметь вид
— в классической модели механики, то функция Гамильтона будет иметь вид
 — квадрат вектора скорости частицы,
— квадрат вектора скорости частицы,  — потенциальная функция, с помощью которой описывается действие на частицу внешних сил
— потенциальная функция, с помощью которой описывается действие на частицу внешних сил  ,
,  — радиус вектор положения частицы. Данные соотношения фактически описывают полную энергию материальной точки, состоящей из кинетической
— радиус вектор положения частицы. Данные соотношения фактически описывают полную энергию материальной точки, состоящей из кинетической  , где
, где  — механический импульс частицы, и потенциальной энергии —
— механический импульс частицы, и потенциальной энергии —  .
. (5)
(5)

 — оператор квадрата импульса. Определение оператора квадрата импульса
— оператор квадрата импульса. Определение оператора квадрата импульса 
 — мнимая единица,
— мнимая единица,  оператор
оператор  в декартовых координатах имеет вид
в декартовых координатах имеет вид
 — орты декартовых осей. Отсюда оператор квадрата импульса будет иметь вид
— орты декартовых осей. Отсюда оператор квадрата импульса будет иметь вид  . Оператор Гамильтона
. Оператор Гамильтона
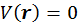 . В случае одномерного движения частицы вдоль оси
. В случае одномерного движения частицы вдоль оси 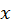 волновую функцию можно записать в виде
волновую функцию можно записать в виде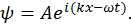
 и формулу Де-Бройля
и формулу Де-Бройля  , выражение для волновой функции можно преобразовать к виду
, выражение для волновой функции можно преобразовать к виду
 имеет вид
имеет вид

 остается открытым. Для того, чтобы установить его, рассмотрим наряду с уравнением Шредингера для описания движения электрона, имеющего заряд
остается открытым. Для того, чтобы установить его, рассмотрим наряду с уравнением Шредингера для описания движения электрона, имеющего заряд  Кл и массу
Кл и массу  ,
,

 — комплексно сопряженная к
— комплексно сопряженная к 

 ,
,  . Уравнение (9) выражает собой хорошо известный из электродинамики закон сохранения заряда, где
. Уравнение (9) выражает собой хорошо известный из электродинамики закон сохранения заряда, где  — плотность заряда,
— плотность заряда,  — плотность тока. Таким образом, полученное из уравнения Шредингера уравнение (9) описывает плотность заряда и плотность тока, возникающую при движении электрона. То есть можно говорить о распределенной в объеме
— плотность тока. Таким образом, полученное из уравнения Шредингера уравнение (9) описывает плотность заряда и плотность тока, возникающую при движении электрона. То есть можно говорить о распределенной в объеме  плотности заряда электрона. Однако полный заряд электрона известен и равен
плотности заряда электрона. Однако полный заряд электрона известен и равен  , поэтому
, поэтому

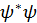 . Равенство интеграла (10) единице означает, что электрон наверняка (с вероятностью, равной единице) находится внутри объема
. Равенство интеграла (10) единице означает, что электрон наверняка (с вероятностью, равной единице) находится внутри объема  , являющегося частью полной области движения
, являющегося частью полной области движения 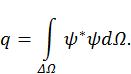

 среднее значение координаты будет равно
среднее значение координаты будет равно
 . Тогда среднее значение этой физической величины будет вычисляться по формуле
. Тогда среднее значение этой физической величины будет вычисляться по формуле
 , в математике носят название самосопряженных. Все операторы физических величин, используемые в теории Шредингера, являются самосопряженными.
, в математике носят название самосопряженных. Все операторы физических величин, используемые в теории Шредингера, являются самосопряженными. ,
, ,
, — функции,
— функции, 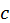 — константа.
— константа. и собственными числами
и собственными числами  оператора
оператора  ,
, — целое положительное число, в общем случае может изменяться в интервале от 1 до бесконечности. Таким образом, оператор может иметь бесконечное число собственных функций и собственных чисел.
— целое положительное число, в общем случае может изменяться в интервале от 1 до бесконечности. Таким образом, оператор может иметь бесконечное число собственных функций и собственных чисел.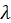 . Вычислим среднее значение оператора
. Вычислим среднее значение оператора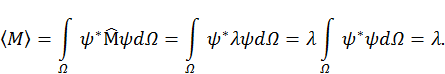

 . Можно показать, что собственные функции операторов физических величин данным свойством обладают. Кроме того в случае самосопряженных операторов, к которым относятся операторы физических величин, их собственные функции обладают свойством ортогональности
. Можно показать, что собственные функции операторов физических величин данным свойством обладают. Кроме того в случае самосопряженных операторов, к которым относятся операторы физических величин, их собственные функции обладают свойством ортогональности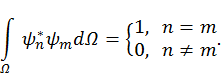

 при
при  , будут равны нулю, остальные единице. Поэтому получим
, будут равны нулю, остальные единице. Поэтому получим
 как вероятность обнаружить квантовый объект в состоянии
как вероятность обнаружить квантовый объект в состоянии 
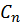 .
.


