 Рис. 2. Потенциальная функция в задаче о потенциальной яме
Рис. 2. Потенциальная функция в задаче о потенциальной яме
|
В качестве первого примера рассмотрим стационарное движение частицы в одномерной потенциальной яме шириной
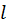
, ограниченной бесконечно высокими стенками. Потенциальную функцию для этого случая можно представить в виде (см. рис. 2)
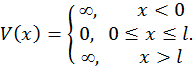
Как видно из данной формулы потенциальная функция на всем отрезке движения частицы равна нулю. При этом стационарное уравнение Шредингера будет иметь вид
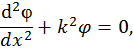
где  . Характеристическое уравнение для данного дифференциального уравнения
. Характеристическое уравнение для данного дифференциального уравнения  имеет два корня
имеет два корня  . Решение уравнения будет иметь вид
. Решение уравнения будет иметь вид  . Неизвестные постоянные
. Неизвестные постоянные  и
и  найдем, используя граничные условия
найдем, используя граничные условия  и
и  , выражающие собой условия непроницаемости стенок потенциальной ямы для частицы. Первое из приведенных условий дает уравнение
, выражающие собой условия непроницаемости стенок потенциальной ямы для частицы. Первое из приведенных условий дает уравнение  , откуда
, откуда  и
и 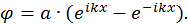
Используя формулу Эйлера, связывающую экспоненциальные и тригонометрические функции  , преобразуем найденное решение к виду
, преобразуем найденное решение к виду
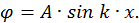
Второе граничное условие дает уравнение  , решение которого есть
, решение которого есть

где  . Откуда
. Откуда  и
и
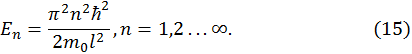
Следовательно, энергия частицы, находящейся в потенциальной яме принимает не любые значения, а образует дискретный спектр разрешенных значений, определяемых формулой (15).
Учитывая, что энергия и импульс частицы связаны соотношением  , можно рассчитать спектр значений импульса частицы
, можно рассчитать спектр значений импульса частицы
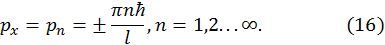
Общий вывод состоит в том, что при движении частицы в замкнутой области, наличии условий, ограничивающих ее движение, возникает эффект квантования характеристик движения частицы — энергии и импульса. Иными словами эти характеристики принимают не любые, а лишь разрешенные соответствующими соотношениями значения.
После подстановки 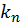 в последнее выражение для волновой функции
в последнее выражение для волновой функции  получим
получим
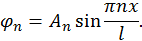
Наконец, остается найти постоянную  в последнем выражении. Для этого воспользуемся условием нормировки (10). Имеем
в последнем выражении. Для этого воспользуемся условием нормировки (10). Имеем

откуда 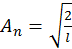 . На рис. 3 построены распределения плотности вероятности
. На рис. 3 построены распределения плотности вероятности  и энергетические уровни частицы для
и энергетические уровни частицы для  и
и 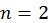 . Значению квантового числа
. Значению квантового числа  соответствует низший уровень энергии частицы. Такое состояние квантового объекта, при котором его энергия имеет минимальное из возможных значений, называются основным состоянием. Из рис. 3 видно, что в основном состоянии график плотности вероятности имеет максимум в точке
соответствует низший уровень энергии частицы. Такое состояние квантового объекта, при котором его энергия имеет минимальное из возможных значений, называются основным состоянием. Из рис. 3 видно, что в основном состоянии график плотности вероятности имеет максимум в точке 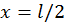 . Это означает, что наиболее вероятная точка появления частицы находится посредине потенциальной ямы. С увеличением квантового числа n количество максимумов плотности вероятности на отрезке
. Это означает, что наиболее вероятная точка появления частицы находится посредине потенциальной ямы. С увеличением квантового числа n количество максимумов плотности вероятности на отрезке  возрастает, что в частности видно из представленных на рис. 3 кривых, построенных для
возрастает, что в частности видно из представленных на рис. 3 кривых, построенных для 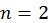 .
.

|
| Рис. 3. Зависимости плотности вероятности от координаты и схема энергетических уровней частицы, «запертой» в потенциальной яме
|
По найденной волновой функции φ можно вычислить средние значения операторов физических величин, используя стандартную формулу
 .
.
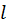 , ограниченной бесконечно высокими стенками. Потенциальную функцию для этого случая можно представить в виде (см. рис. 2)
, ограниченной бесконечно высокими стенками. Потенциальную функцию для этого случая можно представить в виде (см. рис. 2)

 Рис. 2. Потенциальная функция в задаче о потенциальной яме
Рис. 2. Потенциальная функция в задаче о потенциальной яме
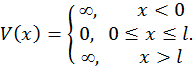
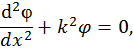
 . Характеристическое уравнение для данного дифференциального уравнения
. Характеристическое уравнение для данного дифференциального уравнения  имеет два корня
имеет два корня  . Решение уравнения будет иметь вид
. Решение уравнения будет иметь вид  . Неизвестные постоянные
. Неизвестные постоянные  и
и  найдем, используя граничные условия
найдем, используя граничные условия  и
и  , выражающие собой условия непроницаемости стенок потенциальной ямы для частицы. Первое из приведенных условий дает уравнение
, выражающие собой условия непроницаемости стенок потенциальной ямы для частицы. Первое из приведенных условий дает уравнение  , откуда
, откуда  и
и 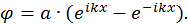
 , преобразуем найденное решение к виду
, преобразуем найденное решение к виду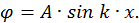
 , решение которого есть
, решение которого есть
 . Откуда
. Откуда  и
и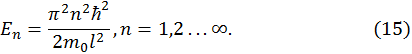
 , можно рассчитать спектр значений импульса частицы
, можно рассчитать спектр значений импульса частицы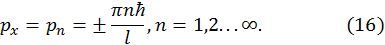
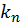 в последнее выражение для волновой функции
в последнее выражение для волновой функции  получим
получим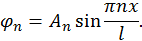
 в последнем выражении. Для этого воспользуемся условием нормировки (10). Имеем
в последнем выражении. Для этого воспользуемся условием нормировки (10). Имеем
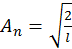 . На рис. 3 построены распределения плотности вероятности
. На рис. 3 построены распределения плотности вероятности  и энергетические уровни частицы для
и энергетические уровни частицы для  и
и 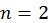 . Значению квантового числа
. Значению квантового числа 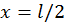 . Это означает, что наиболее вероятная точка появления частицы находится посредине потенциальной ямы. С увеличением квантового числа n количество максимумов плотности вероятности на отрезке
. Это означает, что наиболее вероятная точка появления частицы находится посредине потенциальной ямы. С увеличением квантового числа n количество максимумов плотности вероятности на отрезке  возрастает, что в частности видно из представленных на рис. 3 кривых, построенных для
возрастает, что в частности видно из представленных на рис. 3 кривых, построенных для 
 .
.


