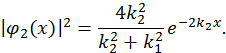В предыдущем примере движение частицы по оси x ограничивалось бесконечно высокими потенциальными барьерами, вследствие чего частица была «заперта» внутри потенциальной ямы. Рассмотрим, как влияет на движение частицы потенциальный барьер конечной высоты. В качестве первого примера рассмотрим взаимодействие частицы с потенциальным барьером ступенчатой формы. График соответствующей потенциальной функции показан на рис. 4.
В данной задаче можно выделить две области — область слева от барьера ( ), где потенциальная функция
), где потенциальная функция  , и область, где
, и область, где  , в которой потенциал имеет постоянное значение
, в которой потенциал имеет постоянное значение  . Рассмотрим вначале случай, когда энергия частицы
. Рассмотрим вначале случай, когда энергия частицы  . При этом стационарное уравнение Шредингера в каждой из областей соответственно будет иметь вид
. При этом стационарное уравнение Шредингера в каждой из областей соответственно будет иметь вид


где 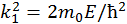 ,
,  . Данные уравнения решаются аналогично предыдущему примеру, при этом получим в первой области
. Данные уравнения решаются аналогично предыдущему примеру, при этом получим в первой области

во второй области

В полученных выражениях коэффициенты  и
и  есть амплитуды падающей, распространяющейся в положительном направлении оси
есть амплитуды падающей, распространяющейся в положительном направлении оси 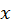 , волны, а
, волны, а  и
и  — амплитуды отраженных, движущихся в обратном направлении волн. Примем амплитуду падающей из точки
— амплитуды отраженных, движущихся в обратном направлении волн. Примем амплитуду падающей из точки  волны равной 1. Поскольку потенциальный рельеф (рис. 4) при
волны равной 1. Поскольку потенциальный рельеф (рис. 4) при  не изменяется, потенциальная функция остается постоянной, то амплитуда отраженной из этой области волны должна быть равна нулю
не изменяется, потенциальная функция остается постоянной, то амплитуда отраженной из этой области волны должна быть равна нулю  . Поэтому решение можно переписать в виде
. Поэтому решение можно переписать в виде


Для определения оставшихся постоянных примем к сведению, что функция  , будучи решением дифференциального уравнения второго порядка должна быть непрерывна вместе со своей первой производной. Поэтому на границе областей в точке
, будучи решением дифференциального уравнения второго порядка должна быть непрерывна вместе со своей первой производной. Поэтому на границе областей в точке  следует потребовать выполнения следующих равенств
следует потребовать выполнения следующих равенств

,
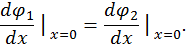
Соотношения (17) носят названия условий «сшивания» решений. Подставляя в (17) последние выражения для  и
и  , получим уравнения относительно неизвестных постоянных
, получим уравнения относительно неизвестных постоянных



|
| Рис. 4. Схема энергетических уровней и форма потенциального рельефа в задаче о ступенчатом потенциальном барьере
|
Решая последнюю систему уравнений относительно неизвестных постоянных, найдем

Для того, чтобы придать более ясный физический смысл полученному решению, вернемся к формуле (9) и выражению для плотности тока, которое в рассматриваемом случае одномерного движения получит вид
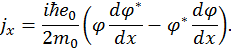
Подставляя вместо  в последнюю формулу
в последнюю формулу  , получим плотность тока, создаваемого падающей электронной волной
, получим плотность тока, создаваемого падающей электронной волной

и для плотности тока отраженной волны 

Вычисляя отношение  , найдем коэффициент отражения барьера
, найдем коэффициент отражения барьера

который оказался равным квадрату амплитуды отраженной волны. В результате данного расчета мы обнаружили чисто квантовый эффект. Несмотря на то, что энергия частицы Е больше высоты потенциального барьера, возникает обратный поток, вызванный присутствием потенциального барьера. Данный эффект получил название надбарьерного отражения.
Рассмотрим эту же задачу для случая  . В области
. В области  уравнение Шредингера сохранит свой вид, а в области
уравнение Шредингера сохранит свой вид, а в области  запишется в виде
запишется в виде

где  . Теперь решение уравнения Шредингера в области барьера будет выглядеть как
. Теперь решение уравнения Шредингера в области барьера будет выглядеть как

Для того чтобы при  решение оставалось ограниченным, следует положить
решение оставалось ограниченным, следует положить  . Применяя теперь условия «сшивания» (17), получим систему уравнений относительно неизвестных постоянных
. Применяя теперь условия «сшивания» (17), получим систему уравнений относительно неизвестных постоянных


в результате решения которой получим
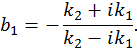
Коэффициент отражения
 .
.
Таким образом, в рассматриваемом случае  имеет место полное отражение и то обстоятельство, что
имеет место полное отражение и то обстоятельство, что  позволяет дать и вероятностную трактовку коэффициента отражения, как вероятности отражения частицы барьером.
позволяет дать и вероятностную трактовку коэффициента отражения, как вероятности отражения частицы барьером.
Постоянная  из последней системы уравнений найдется как
из последней системы уравнений найдется как

Таким образом, внутри барьера будет иметь место отличная от нуля плотность вероятности, равная
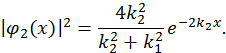
При наличии полного отражения ( ) этот результат можно интерпретировать, как то обстоятельство, что частица, прежде чем отразиться барьером, может проникнуть в него на некоторую глубину.
) этот результат можно интерпретировать, как то обстоятельство, что частица, прежде чем отразиться барьером, может проникнуть в него на некоторую глубину.
 ,
,

 ), где потенциальная функция
), где потенциальная функция  , и область, где
, и область, где  , в которой потенциал имеет постоянное значение
, в которой потенциал имеет постоянное значение  . Рассмотрим вначале случай, когда энергия частицы
. Рассмотрим вначале случай, когда энергия частицы  . При этом стационарное уравнение Шредингера в каждой из областей соответственно будет иметь вид
. При этом стационарное уравнение Шредингера в каждой из областей соответственно будет иметь вид

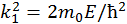 ,
,  . Данные уравнения решаются аналогично предыдущему примеру, при этом получим в первой области
. Данные уравнения решаются аналогично предыдущему примеру, при этом получим в первой области

 и
и  есть амплитуды падающей, распространяющейся в положительном направлении оси
есть амплитуды падающей, распространяющейся в положительном направлении оси 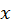 , волны, а
, волны, а  и
и  — амплитуды отраженных, движущихся в обратном направлении волн. Примем амплитуду падающей из точки
— амплитуды отраженных, движущихся в обратном направлении волн. Примем амплитуду падающей из точки  волны равной 1. Поскольку потенциальный рельеф (рис. 4) при
волны равной 1. Поскольку потенциальный рельеф (рис. 4) при  не изменяется, потенциальная функция остается постоянной, то амплитуда отраженной из этой области волны должна быть равна нулю
не изменяется, потенциальная функция остается постоянной, то амплитуда отраженной из этой области волны должна быть равна нулю  . Поэтому решение можно переписать в виде
. Поэтому решение можно переписать в виде

 , будучи решением дифференциального уравнения второго порядка должна быть непрерывна вместе со своей первой производной. Поэтому на границе областей в точке
, будучи решением дифференциального уравнения второго порядка должна быть непрерывна вместе со своей первой производной. Поэтому на границе областей в точке  следует потребовать выполнения следующих равенств
следует потребовать выполнения следующих равенств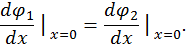
 и
и  , получим уравнения относительно неизвестных постоянных
, получим уравнения относительно неизвестных постоянных



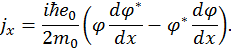
 , получим плотность тока, создаваемого падающей электронной волной
, получим плотность тока, создаваемого падающей электронной волной


 , найдем коэффициент отражения барьера
, найдем коэффициент отражения барьера
 . В области
. В области  уравнение Шредингера сохранит свой вид, а в области
уравнение Шредингера сохранит свой вид, а в области 
 . Теперь решение уравнения Шредингера в области барьера будет выглядеть как
. Теперь решение уравнения Шредингера в области барьера будет выглядеть как
 . Применяя теперь условия «сшивания» (17), получим систему уравнений относительно неизвестных постоянных
. Применяя теперь условия «сшивания» (17), получим систему уравнений относительно неизвестных постоянных

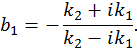
 .
. позволяет дать и вероятностную трактовку коэффициента отражения, как вероятности отражения частицы барьером.
позволяет дать и вероятностную трактовку коэффициента отражения, как вероятности отражения частицы барьером.