Потенциальный барьер прямоугольной формы
Задача о прямоугольном потенциальном барьере, допуская точное и простое по форме решение, в то же время весьма важна при рассмотрении ряда физических явлений, таких, как возникновение электрического тока и пробой твердых и жидких диэлектриков. Указанные явления инициируются туннельным эффектом в потенциальных барьерах, образованных структурой указанных сред. График потенциальной функции для рассматриваемого примера показан на рис. 5. При этом потенциальная функция задается следующей формулой
Область решения целесообразно разбить на три подобласти, как показано на рис. 5. При этом уравнение Шредингера для первой и третьей подобласти будет выглядеть одинаково, поскольку в них потенциальная функция равна нулю
где

где
Поскольку постоянные
Для отыскания оставшихся неизвестными постоянных воспользуемся условиями «сшивания» решений на границах подобластей в точках
Подставляя в эти уравнения последние выражения для волновой функции в подобластях, получим систему уравнений относительно неизвестных постоянных
Из последних двух уравнений найдем
Из первых двух уравнений системы (18) исключим
Подставив в последнее уравнение полученные только что выражения для
Рассуждая также как и в случае ступенчатого потенциального барьера, рассмотренного в предыдущем примере, нетрудно установить, что отношение падающего на барьер электронного тока к прошедшему сквозь него будет равно
Точной формуле (19) можно придать более простой вид в случае достаточно широкого барьера, когда
После подстановки в последнюю формулу выражений для
где Коэффициент отражения барьера, как в предыдущем примере будет равен
После подстановки выражения для a 3 находим
откуда
Складывая коэффициенты прозрачности Последнее выражение еще раз подтверждает вероятностную интерпретацию этих коэффициентов, как вероятности отражения частицы барьером и вероятности прохождения частицей барьера. Ясно что, вероятность полного события отражения или прохождения частицей барьера равна 1, так имеет место только два этих исхода, что и подтверждает полученное равенство. Отметим два существенных квантовомеханических вывода, которые можно сделать по результатам решения этой задачи. Во-первых, мы увидели вероятностный, недетерминированный характер взаимодействия частицы с барьером, ибо возможны оба исхода, как прохождение, так и отражение.
 меньшей, чем энергия барьера меньшей, чем энергия барьера  существует отличная от нуля вероятность преодоления частицей барьера. Это явление носит название туннельного эффекта. существует отличная от нуля вероятность преодоления частицей барьера. Это явление носит название туннельного эффекта.
|


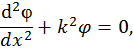
 . Далее мы будем рассматривать лишь случай
. Далее мы будем рассматривать лишь случай  . Поэтому уравнение Шредингера во второй области запишется в виде
. Поэтому уравнение Шредингера во второй области запишется в виде Рис. 5. Потенциальная функция, энергетический уровень и волновая функции частицы при взаимодействии с потенциальным барьером прямоугольной формы
Рис. 5. Потенциальная функция, энергетический уровень и волновая функции частицы при взаимодействии с потенциальным барьером прямоугольной формы
 , где
, где 


 еще не определены, то для удобства решения волновую функцию в третьей области можно записать относительно аргумента
еще не определены, то для удобства решения волновую функцию в третьей области можно записать относительно аргумента  . Как и в предыдущем примере, амплитуду падающей волны полагаем раной единице, а амплитуду, отраженной из бесконечности волны, равной нулю. Тогда решение примет вид
. Как и в предыдущем примере, амплитуду падающей волны полагаем раной единице, а амплитуду, отраженной из бесконечности волны, равной нулю. Тогда решение примет вид
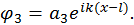
 и
и  :
: ,
, ,
, , (18)
, (18) .
.

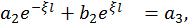
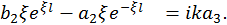
 и
и  :
:

 :
:
 и
и 
 . Данная величина носит название коэффициента прозрачности
. Данная величина носит название коэффициента прозрачности  . После подстановки выражения для
. После подстановки выражения для  имеем:
имеем:
 . В этом случае
. В этом случае ,
,  и
и  .
. и
и  и преобразований получим
и преобразований получим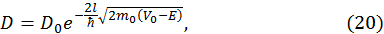
 .
.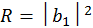 . Постоянную
. Постоянную  . Откуда
. Откуда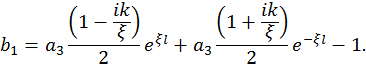


 и отражения
и отражения  , после преобразований с помощью тождества
, после преобразований с помощью тождества  убеждаемся, что
убеждаемся, что  .
. Рис. 6. Взаимодействие частицы с энергией E с потенциальным барьером произвольной формы
Рис. 6. Взаимодействие частицы с энергией E с потенциальным барьером произвольной формы



