В данном разделе с позиций квантовой теории рассматриваются элементарные процессы возникновения и поглощения излучения. Фундаментальным фактом здесь является то, что при переходе квантовой системы (атома, молекулы) в состояние с меньшей энергией избыточная энергия излучается в виде кванта излучения — электромагнитной волны с некоторой частотой колебаний 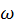 . Также возможен и обратный процесс, когда атом или молекула поглощает энергию внешней электромагнитной волны. При этом электрон переходит на более высокие энергетические уровни по сравнению с начальным. Таким образом, возникновение и поглощение излучения в материальных средах связано с изменением энергетического состояния атомов и молекул, их составляющих. Если электрон в атоме переходит из энергетического состояния
. Также возможен и обратный процесс, когда атом или молекула поглощает энергию внешней электромагнитной волны. При этом электрон переходит на более высокие энергетические уровни по сравнению с начальным. Таким образом, возникновение и поглощение излучения в материальных средах связано с изменением энергетического состояния атомов и молекул, их составляющих. Если электрон в атоме переходит из энергетического состояния  в состояние
в состояние  , то разница
, то разница 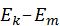 , либо излучается, когда
, либо излучается, когда  , либо поглощается в случае
, либо поглощается в случае  в виде кванта электромагнитной энергии, равного согласно формуле Планка
в виде кванта электромагнитной энергии, равного согласно формуле Планка
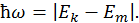
Подобного рода переходы являются частным случаем изменения квантового состояния частицы, под которым понимается изменение набора квантовых чисел, описывающих ее состояние. Мы видели в предыдущем разделе, что уже в мало-мальски сложных квантовых объектах состояние частицы фиксируется несколькими квантовыми числами. Переходом, таким образом, является изменение значения как минимум одного из них.
Вторым фундаментальным свойством квантовых переходов является наличие «запрещенных» квантовых переходов, вероятность которых существенно меньше так называемых «разрешенных» переходов. Это означает, что атомы и молекулы способны излучать и поглощать электромагнитные волны не любой частоты, а только тех, которые удовлетворяют правилу отбора. Если переход  является разрешенным, то будет излучаться или поглощаться электромагнитная волна соответствующей частоты
является разрешенным, то будет излучаться или поглощаться электромагнитная волна соответствующей частоты  .
.
Возникновения правила отбора при взаимодействии излучения с электроном в атоме рассмотрим с помощью уравнении Шредингера. Пусть атом находится в поле электромагнитной волны частоты 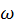 , напряженность электрического поля которой направлена вдоль оси
, напряженность электрического поля которой направлена вдоль оси 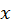 . При этом длину электромагнитной волны λ будем полагать существенно большей размера атома
. При этом длину электромагнитной волны λ будем полагать существенно большей размера атома  м. Для оптического диапазона электромагнитного излучения
м. Для оптического диапазона электромагнитного излучения  м. Поэтому напряженность электрического поля, действующего на электрон, можно задать с помощью формулы
м. Поэтому напряженность электрического поля, действующего на электрон, можно задать с помощью формулы  , где
, где  — амплитуда,
— амплитуда, 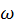 — частота. Соответственно сила, действующая на электрон со стороны поля
— частота. Соответственно сила, действующая на электрон со стороны поля  , а ее потенциал
, а ее потенциал
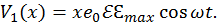
Таким образом, потенциальная функция электрона будет состоять из двух частей  , определяющей силовое взаимодействие электрона и ядра, и
, определяющей силовое взаимодействие электрона и ядра, и  , описывающей силовое воздействие внешней электромагнитной волны.
, описывающей силовое воздействие внешней электромагнитной волны.
Поскольку здесь анализируется переход электрона из одного квантового состояния в другое, мы не можем пользоваться стационарным уравнением Шредингера, а должны применить его в общей форме
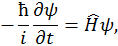
где гамильтониан  будет наряду с основной частью
будет наряду с основной частью  , описывающий взаимодействие электрона и ядра в отсутствие внешних полей, иметь и составляющую
, описывающий взаимодействие электрона и ядра в отсутствие внешних полей, иметь и составляющую 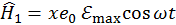 :
:
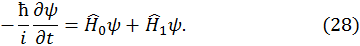
В исходном состоянии до появления электромагнитной волны 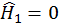 частные решения уравнения (28) могут быть представлены, как это мы делали выше в виде
частные решения уравнения (28) могут быть представлены, как это мы делали выше в виде
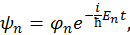
где 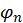 — частные решения стационарного уравнения Шредингера. Решение возмущенного (
— частные решения стационарного уравнения Шредингера. Решение возмущенного ( ) уравнения (28) будем искать в виде разложения по функциям
) уравнения (28) будем искать в виде разложения по функциям  :
:
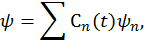
где  — коэффициенты, зависящие от времени. Подставляя это разложение в (28), получим
— коэффициенты, зависящие от времени. Подставляя это разложение в (28), получим
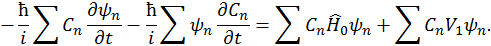
Поскольку каждое частное  решение само по себе удовлетворяет невозмущенному уравнению
решение само по себе удовлетворяет невозмущенному уравнению
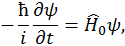
то первые члены справа и слева в предыдущей записи взаимно уничтожаются, и мы получаем
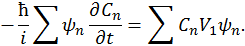
Домножим получившееся уравнение на  и проинтегрируем по всему объему
и проинтегрируем по всему объему  . При этом учтем, что в силу рассмотренного ранее свойства ортогональности системы функций, образуемой частными решениями невозмущенного уравнения Шредингера, интегралы
. При этом учтем, что в силу рассмотренного ранее свойства ортогональности системы функций, образуемой частными решениями невозмущенного уравнения Шредингера, интегралы
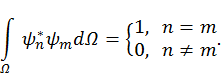
Поэтому получим
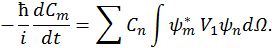
Мы пришли к системе уравнений относительно коэффициентов  , число которых в общем случае неограниченно. Поэтому точное ее решение представляется затруднительным. Однако приближенный анализ данной системы позволит ответить на вопрос о возникновении правила отбора. Предположим, что до начала перехода система находилась в некотором стационарном состоянии
, число которых в общем случае неограниченно. Поэтому точное ее решение представляется затруднительным. Однако приближенный анализ данной системы позволит ответить на вопрос о возникновении правила отбора. Предположим, что до начала перехода система находилась в некотором стационарном состоянии  . Тогда под знаком суммы все коэффициенты, включая
. Тогда под знаком суммы все коэффициенты, включая  , кроме
, кроме 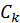 равны нулю. Появление изменений в коэффициенте
равны нулю. Появление изменений в коэффициенте  , т. е. его изменение от нулевого значения к некоторому, отличному от нуля, будет означать переход из состояния
, т. е. его изменение от нулевого значения к некоторому, отличному от нуля, будет означать переход из состояния  в состояние
в состояние  . В состоянии системы, близком начальному, мы можем записать
. В состоянии системы, близком начальному, мы можем записать
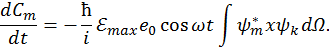
Здесь для нас представляет интерес интеграл в правой части, поскольку именно в нем заключены волновые функции, отвечающие двум различным квантовым состояниям. Если этот интеграл тождественно равен нулю, то и переход из состояния  в состояние
в состояние  невозможен, поскольку первоначально равный нулю
невозможен, поскольку первоначально равный нулю  изменяться не будет, и система сохранится в состоянии
изменяться не будет, и система сохранится в состоянии  . Таким образом, мы можем сформулировать правило отбора. Если называемая матричным элементом величина
. Таким образом, мы можем сформулировать правило отбора. Если называемая матричным элементом величина

равна нулю, то переход из состояния  в состояние
в состояние  запрещен. Напомним, что эти запреты не носят абсолютного характера. Речь идет о весьма малой вероятности таких переходов по сравнению с разрешенными. В частности время ожидания разрешенного перехода составляет
запрещен. Напомним, что эти запреты не носят абсолютного характера. Речь идет о весьма малой вероятности таких переходов по сравнению с разрешенными. В частности время ожидания разрешенного перехода составляет 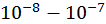 с, в то время как запрещенный переход реализуется за время
с, в то время как запрещенный переход реализуется за время  с.
с.
Рассмотрим простейшие примеры. Проанализируем правило отбора переходов при изменении магнитного квантового числа  в атоме водорода.
в атоме водорода.
Ранее мы получили волновую функцию электрона в атоме водорода в виде
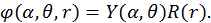
Причем для первого сомножителя в правой части было найдено
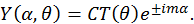
Магнитное квантовое число фигурирует только в показателе экспоненты последнего выражения. Поэтому для проверки на нулевое значение матричного элемента для перехода из состояния с магнитным квантовым числом  в состояние с магнитным квантовым числом
в состояние с магнитным квантовым числом  нам достаточно вычислить интеграл
нам достаточно вычислить интеграл
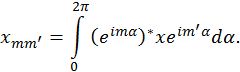
Поскольку 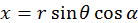 , то
, то
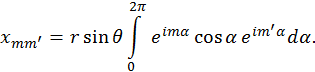
Непосредственно вычисляя интеграл в правой части уравнений, для чего можно представить тригонометрическую функцию с помощью экспонент с комплексными показателями, убеждаемся, что он будет отличен от нуля только в случае, если 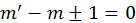 . Это означает, что при переходе в состояние с иным значением магнитного квантового числа, последнее не может измениться более чем на единицу.
. Это означает, что при переходе в состояние с иным значением магнитного квантового числа, последнее не может измениться более чем на единицу.
Используя выражения других декартовых координат через сферические  ,
,  , нетрудно рассчитать матричные элементы для других направлений электрического поля внешней волны. При этом
, нетрудно рассчитать матричные элементы для других направлений электрического поля внешней волны. При этом  ведет себя аналогично
ведет себя аналогично  , запрещая переходы с
, запрещая переходы с  .
.
Элемент  отличен от нуля только при
отличен от нуля только при  , т. е. запрещает все переходы по магнитному квантовому числу при направлении внешнего поля параллельном оси вращения электрона.
, т. е. запрещает все переходы по магнитному квантовому числу при направлении внешнего поля параллельном оси вращения электрона.

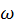 . Также возможен и обратный процесс, когда атом или молекула поглощает энергию внешней электромагнитной волны. При этом электрон переходит на более высокие энергетические уровни по сравнению с начальным. Таким образом, возникновение и поглощение излучения в материальных средах связано с изменением энергетического состояния атомов и молекул, их составляющих. Если электрон в атоме переходит из энергетического состояния
. Также возможен и обратный процесс, когда атом или молекула поглощает энергию внешней электромагнитной волны. При этом электрон переходит на более высокие энергетические уровни по сравнению с начальным. Таким образом, возникновение и поглощение излучения в материальных средах связано с изменением энергетического состояния атомов и молекул, их составляющих. Если электрон в атоме переходит из энергетического состояния  в состояние
в состояние  , то разница
, то разница 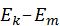 , либо излучается, когда
, либо излучается, когда  , либо поглощается в случае
, либо поглощается в случае  в виде кванта электромагнитной энергии, равного согласно формуле Планка
в виде кванта электромагнитной энергии, равного согласно формуле Планка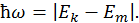
 является разрешенным, то будет излучаться или поглощаться электромагнитная волна соответствующей частоты
является разрешенным, то будет излучаться или поглощаться электромагнитная волна соответствующей частоты  .
.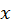 . При этом длину электромагнитной волны λ будем полагать существенно большей размера атома
. При этом длину электромагнитной волны λ будем полагать существенно большей размера атома  м. Для оптического диапазона электромагнитного излучения
м. Для оптического диапазона электромагнитного излучения  м. Поэтому напряженность электрического поля, действующего на электрон, можно задать с помощью формулы
м. Поэтому напряженность электрического поля, действующего на электрон, можно задать с помощью формулы  , где
, где  — амплитуда,
— амплитуда,  , а ее потенциал
, а ее потенциал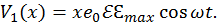
 , определяющей силовое взаимодействие электрона и ядра, и
, определяющей силовое взаимодействие электрона и ядра, и  , описывающей силовое воздействие внешней электромагнитной волны.
, описывающей силовое воздействие внешней электромагнитной волны.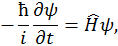
 будет наряду с основной частью
будет наряду с основной частью  , описывающий взаимодействие электрона и ядра в отсутствие внешних полей, иметь и составляющую
, описывающий взаимодействие электрона и ядра в отсутствие внешних полей, иметь и составляющую 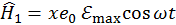 :
: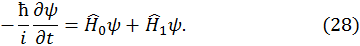
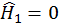 частные решения уравнения (28) могут быть представлены, как это мы делали выше в виде
частные решения уравнения (28) могут быть представлены, как это мы делали выше в виде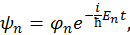
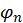 — частные решения стационарного уравнения Шредингера. Решение возмущенного (
— частные решения стационарного уравнения Шредингера. Решение возмущенного ( ) уравнения (28) будем искать в виде разложения по функциям
) уравнения (28) будем искать в виде разложения по функциям  :
: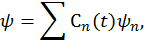
 — коэффициенты, зависящие от времени. Подставляя это разложение в (28), получим
— коэффициенты, зависящие от времени. Подставляя это разложение в (28), получим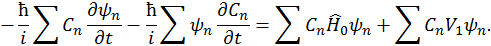
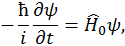
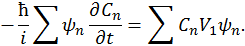
 и проинтегрируем по всему объему
и проинтегрируем по всему объему  . При этом учтем, что в силу рассмотренного ранее свойства ортогональности системы функций, образуемой частными решениями невозмущенного уравнения Шредингера, интегралы
. При этом учтем, что в силу рассмотренного ранее свойства ортогональности системы функций, образуемой частными решениями невозмущенного уравнения Шредингера, интегралы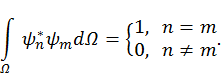
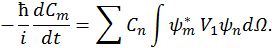
 , число которых в общем случае неограниченно. Поэтому точное ее решение представляется затруднительным. Однако приближенный анализ данной системы позволит ответить на вопрос о возникновении правила отбора. Предположим, что до начала перехода система находилась в некотором стационарном состоянии
, число которых в общем случае неограниченно. Поэтому точное ее решение представляется затруднительным. Однако приближенный анализ данной системы позволит ответить на вопрос о возникновении правила отбора. Предположим, что до начала перехода система находилась в некотором стационарном состоянии  . Тогда под знаком суммы все коэффициенты, включая
. Тогда под знаком суммы все коэффициенты, включая 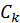 равны нулю. Появление изменений в коэффициенте
равны нулю. Появление изменений в коэффициенте  . В состоянии системы, близком начальному, мы можем записать
. В состоянии системы, близком начальному, мы можем записать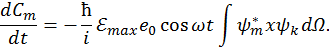

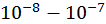 с, в то время как запрещенный переход реализуется за время
с, в то время как запрещенный переход реализуется за время  с.
с.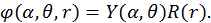
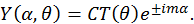
 нам достаточно вычислить интеграл
нам достаточно вычислить интеграл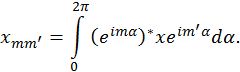
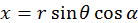 , то
, то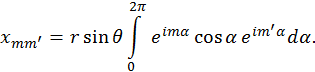
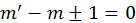 . Это означает, что при переходе в состояние с иным значением магнитного квантового числа, последнее не может измениться более чем на единицу.
. Это означает, что при переходе в состояние с иным значением магнитного квантового числа, последнее не может измениться более чем на единицу. ,
,  , нетрудно рассчитать матричные элементы для других направлений электрического поля внешней волны. При этом
, нетрудно рассчитать матричные элементы для других направлений электрического поля внешней волны. При этом  ведет себя аналогично
ведет себя аналогично  , запрещая переходы с
, запрещая переходы с  .
. отличен от нуля только при
отличен от нуля только при  , т. е. запрещает все переходы по магнитному квантовому числу при направлении внешнего поля параллельном оси вращения электрона.
, т. е. запрещает все переходы по магнитному квантовому числу при направлении внешнего поля параллельном оси вращения электрона.


