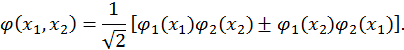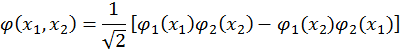МНОГОЭЛЕКТРОННЫЕ КВАНТОВЫЕ СИСТЕМЫ
При переходе к системам с двумя или большим количеством частиц, например, электронов, появляются некоторые новые факты, отражаемые в квантовомеханических постулатах, которые вытекают из эксперимента. Главным постулатом является принцип неразличимости одинаковых по своей природе частиц. Если две частицы находятся на расстоянии, когда их волновые пакеты перекрываются, т. е. на расстоянии порядка длины волны Де-Бройля, то нельзя говорить, что частица 1 находится в окрестности точки Математически принцип неразличимости можно выразить следующим образом. Пусть движение двух частиц описывается волновой функции
В случае знака «+» в последнем соотношении волновая функция называется симметричной, в случае «–» — антисимметричной. Если две частицы совершают одномерное движение вдоль оси x, волновая функция должна удовлетворять соотношению
Например, функция Второй факт, характеризующий поведение квантовой системы из многих частиц, имеющий место независимо от принципа неразличимости, — обменное вырождение. Напомним, что вырождением называется явление, когда одно и то же значение энергии системы, реализуется при различных квантовых состояниях (наборах квантовых чисел). В качестве примера рассмотрим две частицы, совершающие одномерное движение вдоль оси x в потенциальной яме с бесконечно высокими стенками. Потенциальную функцию систему двух частиц при этом можно представить в виде
где
При одномерном движении
Будем искать решение данного уравнения в виде произведения двух функций, каждая из которых зависит только от одной переменной
Если неизвестную постоянную (энергию) представить в виде суммы двух констант
Решение каждого из этих уравнений нам хорошо известно по задаче о движении одной частицы в одномерной потенциальной яме (раздел 1.2):
Отсюда найдем решение исходного уравнения
Квантовые числа
При этом знак «+» соответствует симметричной волновой функции, «–» — антисимметричной. Постоянную α находим с помощью условия нормировки
Подставляя последнее выражение для
Поскольку волновые функции
Частицы, обладающие в системе антисимметричной волновой функцией, называются фермионами. К фермионам относятся частицы с дробным спином, проекция которого принимает значения 1/2, 3/2 и т. д. Частицы с целыми значениями проекции спина 0, 1, 2 и т. д. — бозоны, обладающие симметричной волновой функцией. Фермионами в частности являются электроны, протоны, нейтроны. К бозонам относятся фотоны, дейтоны и другие частицы, содержащие четное число фермионов. Обратим внимание на то, что волновая функция двух фермионов
может быть вычислена как определитель
Нетрудно обобщить эту формулу на случай произвольного числа N фермионов
Если предположить, что какие-либо 2 из N фермионов находятся в одинаковых квантовых состояниях, то это будет означать равенство всех элементов соответствующих строк в выписанном определителе. Например, если первый и N -ый фермионы пребывают в одном квантовом состоянии, то первая и последняя строки определителя равны друг другу. По свойству определителей, определитель, имеющий хотя бы две одинаковые строки, тождественно равен нулю. Таким образом, волновая функция системы фермионов, в которой хотя бы два находятся в одинаковом квантовом состоянии, тождественно равна нулю. Следовательно, такое состояние не реализуемо. Полученный результат в отношении системы фермионов фактически формулирует математически известный принцип запрета Паули для электронов.
|

 , а частица 2 в окрестности точи
, а частица 2 в окрестности точи  , а можно лишь указать, что две частицы находятся в окрестностях точек
, а можно лишь указать, что две частицы находятся в окрестностях точек  и
и  . С точки зрения классической физики в такой системе может быть два состояния: 1) частица 1 имеет энергию
. С точки зрения классической физики в такой системе может быть два состояния: 1) частица 1 имеет энергию  . При этом
. При этом 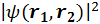 является плотностью вероятности обнаружения частиц в окрестностях точек 1 и 2. Но в силу принципа неразличимости частиц эта функция не должна изменятся при перестановке аргументов местами (теперь первую частицу помещаем в положение 2, а вторую — в положение 1. При этом получим
является плотностью вероятности обнаружения частиц в окрестностях точек 1 и 2. Но в силу принципа неразличимости частиц эта функция не должна изменятся при перестановке аргументов местами (теперь первую частицу помещаем в положение 2, а вторую — в положение 1. При этом получим  . Отсюда следует
. Отсюда следует .
.
 является симметричной, а функция
является симметричной, а функция  — антисимметрична.
— антисимметрична.
 — индивидуальные потенциальные функции частиц,
— индивидуальные потенциальные функции частиц,  — потенциал взаимодействия между частицами.Стационарное уравнение Шредингера для двух частиц можно в общем виде записать, как
— потенциал взаимодействия между частицами.Стационарное уравнение Шредингера для двух частиц можно в общем виде записать, как
 ,
,  . Рассмотрим две невзаимодействующие частицы в одномерной потенциальной яме с бесконечно высокими стенками. При этом
. Рассмотрим две невзаимодействующие частицы в одномерной потенциальной яме с бесконечно высокими стенками. При этом 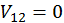 . Тогда уравнение Шредингера получит вид
. Тогда уравнение Шредингера получит вид
 . Подставляя данное представление в предыдущее уравнение и деля на
. Подставляя данное представление в предыдущее уравнение и деля на  , получим
, получим
 , то последнее уравнение можно представить в виде суммы двух независимых уравнений
, то последнее уравнение можно представить в виде суммы двух независимых уравнений
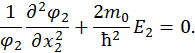
 ,
, 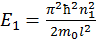 ,
, 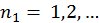
 ,
,  ,
, 


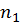 и
и  отличаются друг от друга. Разные комбинации квантовых чисел соответствуют разным квантовым состояниям системы. При этом энергия системы при различных комбинациях квантовых чисел, например
отличаются друг от друга. Разные комбинации квантовых чисел соответствуют разным квантовым состояниям системы. При этом энергия системы при различных комбинациях квантовых чисел, например  ,
,  и
и  ,
,  , может оставаться одной и той же. Следовательно, такой энергетический уровень системы является вырожденным. В общем случае, если первая находится в квантовом состоянии с числом
, может оставаться одной и той же. Следовательно, такой энергетический уровень системы является вырожденным. В общем случае, если первая находится в квантовом состоянии с числом  (энергия при этом не изменилась). Выше мы получили, что для выполнения принципа неразличимости квантовых частиц необходимо, чтобы волновая функция была либо симметрична, либо антисимметрична. Из записанной здесь пары решений можно построить линейную комбинацию, которая данному свойству удовлетворяет, и как любая суперпозиция решений, также является решением исходного уравнения:
(энергия при этом не изменилась). Выше мы получили, что для выполнения принципа неразличимости квантовых частиц необходимо, чтобы волновая функция была либо симметрична, либо антисимметрична. Из записанной здесь пары решений можно построить линейную комбинацию, которая данному свойству удовлетворяет, и как любая суперпозиция решений, также является решением исходного уравнения:

 под знак интеграла, найдем
под знак интеграла, найдем
 и
и  удовлетворяют условию нормировки, то первые два слагаемых в квадратных скобках дают в сумме 2. Третье слагаемое в скобках содержит интегралы от произведения разных волновых функций и в силу свойства ортогональности последних равно нулю. Поэтому получим
удовлетворяют условию нормировки, то первые два слагаемых в квадратных скобках дают в сумме 2. Третье слагаемое в скобках содержит интегралы от произведения разных волновых функций и в силу свойства ортогональности последних равно нулю. Поэтому получим  . Откуда
. Откуда  и
и