Упражнения для самоконтроля
1. Кинетическая энергия электрона равна 1 кэВ. Определить длину волны Де-Бройля. Указания к решению задач: 1–6 — использовать формулу Де-Бройля (раздел 1.1.) и классическое соотношение кинетической энергии частицы с ее импульсом 2. Кинетическая энергия электрона равна 0, 6 МэВ. Определить длину волны Де-Бройля. 3. Определить импульс и энергию электрона, если его длина волны Де-Бройля равна 1 ангстрем. 4. Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны Де-Бройля у него была равна 1м. 5. Рассчитать и построить на графике зависимость длины волны Де-Бройля электрона от величины ускоряющей разности потенциалов, изменяющейся в интервале 20–100 В. 6. Заряженная частица, ускоренная разностью потенциалов 500 В имеет длину волны Де-Бройля 7. Энергия альфа-частиц, испускаемых радием равна Указания к решению задач: 7, 8 — применить первое соотношение неопределенностей формула (1). 8. Электрон «заперт» в области с характерным размером 1 ангстрем. Какова должна быть минимальная энергия электрона, чтобы соотношение неопределенностей было удовлетворено? Выразить эту энергию в джоулях и электрон-вольтах. 9. Определить длину волны фотона, испускаемого при переходе электрона в одномерной потенциальной яме шириной 0, 2 нм из состояния с Указания к решению задачи — применить выражение для энергии частицы в одномерной потенциальной яме, формула (15) и соотношение Де-Бройля. 10. Электрон находится в одномерной потенциальной яме шириной Указания к решению задач: 10–14 — использовать выражения для волновой функции частицы в одномерной потенциальной яме 11. Электрон находится в потенциальной яме шириной 12. Найти среднее значение координаты электрона в потенциальной яме шириной l в основном состоянии. 13. Найти среднее значение импульса электрона, находящегося в потенциальной яме шириной l в основном состоянии. 14. С помощью оператора квадрата импульса найти среднее значение квадрата импульса частицы в потенциальной яме в основном состоянии. 15. Рассчитать и построить на графике зависимость коэффициента отражения потенциального барьера ступенчатой формы для случая, когда энергия частицы E больше высоты барьера Указания к решению задачи — применить соотношения для коэффициента отражения потенциального барьера ступенчатой формы, (раздел 1.4). 16. Прямоугольный потенциальный барьер имеет ширину 0, 1 нм. Разность между высотой потенциального барьера и энергией электрона Указания к решению задач 16–19 — применить выражение для коэффициента прозрачности барьера прямоугольной формы, формула (20). 17. Протон с энергией 5 эВ встречает на своем пути прямоугольный потенциальный барьер высотой 10 эВ и шириной 0, 1 нм. Определить вероятность прохождения протоном этого барьера. 18. Найти коэффициент прозрачности прямоугольного потенциального барьера высотой 2 эВ и шириной 1 ангстрем при его взаимодействии с электроном, обладающим энергией 1эВ. 19. Рассчитать и построить на графике зависимость коэффициента прозрачности прямоугольного потенциального барьера от его ширины, которая может меняться в интервале 1–5 ангстрем для электрона при разности высоты барьера и энергии частицы равной 5 эВ. 20. Рассчитать и построить на графике зависимость коэффициента прозрачности потенциального барьера на границе металл–вакуум для электрона от величины внешнего электрического поля, изменяющегося в пределах Указания к решению задач 20–21 — применить формулу для коэффициента прозрачности барьера произвольной формы, формула (21). 21. Потенциальный барьер имеет форму равнобедренного треугольника с основанием 1 ангстрем и высотой 22. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй. Указания к решению задач 22–23 — использовать формулу энергетического спектра электрона в атоме водорода, формула (27). 23. Найти первый потенциал возбуждения атома водорода. 24. Найти нормировочную константу волновой функции атома водорода в 1s состоянии. Ответ: — применить нормировочное соотношение для волновой функции в сферических координатах 25. Определить вероятность обнаружения электрона в атоме водорода в основном (1s) состоянии внутри сферы Указания к решению задачи — применить интегрирование квадрата волновой функции электрона в основном состоянии 1, 0, 0 в сферических координатах 26. Найти среднее значение радиуса орбиты электрона в атоме водорода в основном (1s) состоянии. Указания к решению задач 26–29 — применить правило вычисления средних значений операторов, формула (12), с использованием сферической системы координат для волновой функции электрона в атоме водорода в основном состоянии 1, 0, 0. 27. Найти среднее значение потенциальной энергии электрона в поле ядра в атоме водорода в 1s состоянии. 28. Найти среднее значение квадрата расстояния между электроном и протоном в атоме водорода в 1s состоянии. 29. Найти наиболее вероятное расстояние между электроном и ядром в атоме водорода в 1s состоянии. 30. Вывести правило отбора в атоме водорода для перехода из состояния с Указания к решению задач 30–31 — применить формулу (29) для вычисления матричныx элементов 31. Исследовать предыдущую задачу при направлении электрического поля вдоль оси x. Ответ: переход запрещен.
|

 .
. м. Принимая заряд частицы равным заряду электрона, определить ее массу.
м. Принимая заряд частицы равным заряду электрона, определить ее массу. эВ. Пользуясь соотношением неопределенностей, выяснить, при какой степени точности определения положения альфа-частицы еще можно пренебречь неопределенностью импульса по сравнению с самой величиной импульса. Приемлемой точностью считать 1 %, масса альфа-частицы 7360 масс электрона.
эВ. Пользуясь соотношением неопределенностей, выяснить, при какой степени точности определения положения альфа-частицы еще можно пренебречь неопределенностью импульса по сравнению с самой величиной импульса. Приемлемой точностью считать 1 %, масса альфа-частицы 7360 масс электрона.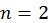 в состояние с наименьшей энергией.
в состояние с наименьшей энергией.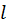 с бесконечно высокими стенками. Определить вероятность обнаружения электрона в средней трети ямы, если электрон находится в возбужденном состоянии с
с бесконечно высокими стенками. Определить вероятность обнаружения электрона в средней трети ямы, если электрон находится в возбужденном состоянии с  .
. выражения для операторов импульса
выражения для операторов импульса  квадрата импульса
квадрата импульса  и формулы для вычисления средних значений операторов, формула (12).
и формулы для вычисления средних значений операторов, формула (12). .
. , от отношения
, от отношения  , которое изменяется в интервале 0–1.
, которое изменяется в интервале 0–1. эВ. Определить во сколько раз изменится коэффициент прозрачности барьера, если указанная разность возрастет в четыре раза.
эВ. Определить во сколько раз изменится коэффициент прозрачности барьера, если указанная разность возрастет в четыре раза. В/м, работа выхода равна 1, 5 эВ.
В/м, работа выхода равна 1, 5 эВ. .
.
 ,
,  — радиус Бора.
— радиус Бора.
 в состояние
в состояние  при напряженности электрического поля, направленной вдоль оси
при напряженности электрического поля, направленной вдоль оси  . Ответ: переход разрешен.
. Ответ: переход разрешен.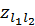 ,
, 



