Рассмотрим малые колебания, распространяющиеся в газе в направлении оси 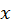 . При одномерном движении первые два уравнения системы (58) принимают вид
. При одномерном движении первые два уравнения системы (58) принимают вид
 , (59)
, (59)
 .
.
Если амплитуда колебаний мала, то мала и скорость движения частиц, поэтому в последних двух уравнениях члены  будут иметь второй порядок малости и их можно отбросить. Рассмотрим адиабатический режим, когда
будут иметь второй порядок малости и их можно отбросить. Рассмотрим адиабатический режим, когда  . Тогда
. Тогда  , где
, где  , где
, где  — начальная плотность,
— начальная плотность,  — начальное давление. Поскольку
— начальное давление. Поскольку  , где
, где  , можно в уравнениях системы (59) приближенно заменить
, можно в уравнениях системы (59) приближенно заменить  на
на  . Кроме того,
. Кроме того,
 ,
,  .
.
После преобразований получаем линеаризованную систему уравнений
 ,
,
 .
.
Исключая  , приходим к волновому уравнению для
, приходим к волновому уравнению для 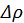 :
:
 ,
,
где  — скорость распространения акустических колебаний (скорость звука). Общее решение полученного уравнения имеет вид, характерный для решений волновых уравнений
— скорость распространения акустических колебаний (скорость звука). Общее решение полученного уравнения имеет вид, характерный для решений волновых уравнений
 .
.
Это возмущение, распространяющееся в положительном (при знаке «–») или в отрицательном (при знаке «+») направлении со скоростью  . Скорость распространения малых колебаний в среде (скорость звука) можно связать с тепловой скоростью частиц
. Скорость распространения малых колебаний в среде (скорость звука) можно связать с тепловой скоростью частиц  . Для газа с тремя степенями свободы (
. Для газа с тремя степенями свободы (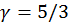 )
)
 ,
,
где T — абсолютная температура, n — концентрация и масса частиц газа. Отсюда видно, что скорость распространения возмущения в газе близка к тепловой скорости частиц.

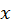 . При одномерном движении первые два уравнения системы (58) принимают вид
. При одномерном движении первые два уравнения системы (58) принимают вид , (59)
, (59) .
. будут иметь второй порядок малости и их можно отбросить. Рассмотрим адиабатический режим, когда
будут иметь второй порядок малости и их можно отбросить. Рассмотрим адиабатический режим, когда  . Тогда
. Тогда  , где
, где  , где
, где  — начальная плотность,
— начальная плотность,  — начальное давление. Поскольку
— начальное давление. Поскольку  , где
, где  , можно в уравнениях системы (59) приближенно заменить
, можно в уравнениях системы (59) приближенно заменить  на
на  . Кроме того,
. Кроме того, ,
,  .
. ,
, .
. , приходим к волновому уравнению для
, приходим к волновому уравнению для 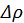 :
: ,
, — скорость распространения акустических колебаний (скорость звука). Общее решение полученного уравнения имеет вид, характерный для решений волновых уравнений
— скорость распространения акустических колебаний (скорость звука). Общее решение полученного уравнения имеет вид, характерный для решений волновых уравнений .
. . Скорость распространения малых колебаний в среде (скорость звука) можно связать с тепловой скоростью частиц
. Скорость распространения малых колебаний в среде (скорость звука) можно связать с тепловой скоростью частиц  . Для газа с тремя степенями свободы (
. Для газа с тремя степенями свободы (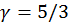 )
) ,
,


