Уравнения движения и распространения колебаний в деформируемом твердом теле
Система уравнений (66) совместно с соотношениями, связывающими напряжения и деформации (65), и между деформациями и перемещениями может быть решена относительно перемещений, по которым могут быть вычислены все необходимые характеристики напряженного состояния в точках твердого тела — перемещения, деформации и напряжения. Рассмотрим на основе представленной выше математической модели распространение волн в упругой сплошной среде. Данная задача представляет интерес при проектировании устройств, предназначенных для ударной очистки поверхностей от инородных веществ, когда с помощью импульсного электромагнитного устройства в упругой среде возбуждаются волны механических колебаний необходимой интенсивности. В процессе распространения такой волны вдоль границы раздела металла и загрязнения возникают механические напряжения, достаточные для разрушения этого механического контакта.
В качестве первого примера рассмотрим распространение плоской упругой волны в неограниченном пространстве вдоль оси x. При этом оси y и z можно сориентировать в плоскости, перпендикулярной оси x, таким образом, что компонента вектора перемещения, перпендикулярная направлению распространения волны, будет иметь лишь одну отличную от нуля проекцию, например, Как видно из рис. 33, при распространении упругой волны имеет место два типа смещений в среде. Для первого типа характерно смещение частиц (
Компоненты тензора деформации в соответствии со сделанными предположениями будут иметь следующий вид
При разложении на шар и девиатор получим
Далее по закону Гука
Складывая тензоры, получим для напряжений
При этом уравнения динамики примут вид
где
В курсе теории упругости доказывается, что вектор перемещения
где в качестве скорости распространения c фигурирует соответствующая выбранному вектору либо продольная Рассмотрим теперь распространение упругих волн вдоль поверхности упругой сплошной среды. Поскольку в данном примере область распространения волны является полупространством, ограниченным плоскостью x 0 z, то искомые компоненты вектора перемещений зависят от двух пространственных переменных. Компонента некоторого вектора перемещений в общем случае представима в виде функции
Будем искать решение последнего уравнения в виде плоской волны, распространяющейся вдоль оси x, амплитуда которой зависит от удаления от поверхности полупространства, т. е. от y:
где k и ω — соответственно волновое число и круговая частота колебаний упругой волны, i — мнимая единица. Подставляя последнее выражение в (67), получим дифференциальное уравнение относительно f (y):
В зависимости от знака выражения Это объясняется тем, что энергия упругих деформаций концентрируется в относительно тонком слое вблизи поверхности, а не рассеивается при распространении волны в глубину полупространства. Поэтому при использовании поверхностной волны в технологических процессах весьма важно, чтобы доля низкочастотных составляющих в волновом спектре, для которых
|


 (рис. 33).
(рис. 33). ) упругого тела вдоль линии распространения волны — продольные колебания. Второй тип колебаний создается поперечными по отношению к линии распространения волны смещениями (
) упругого тела вдоль линии распространения волны — продольные колебания. Второй тип колебаний создается поперечными по отношению к линии распространения волны смещениями (
 .
. ,
,  .
.
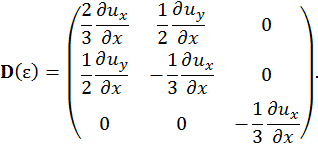

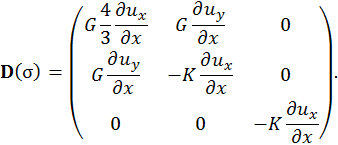
 ,
,  .
.
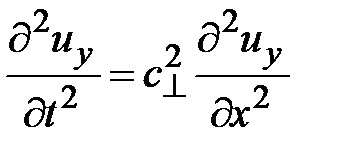 ,
, ,
,  — параметры, определяющие скорости распространения колебаний в упругой среде, поскольку полученные уравнения являются волновыми уравнениями относительно компонент вектора перемещений
— параметры, определяющие скорости распространения колебаний в упругой среде, поскольку полученные уравнения являются волновыми уравнениями относительно компонент вектора перемещений  можно интерпретировать, как скорость распространения продольных, а
можно интерпретировать, как скорость распространения продольных, а  — поперечных колебаний. Поскольку
— поперечных колебаний. Поскольку  , то продольные колебания распространяются несколько быстрее, чем поперечные. Общее решение волновых уравнений, как обычно, представляется в виде
, то продольные колебания распространяются несколько быстрее, чем поперечные. Общее решение волновых уравнений, как обычно, представляется в виде ,
,  .
. всегда может быть представлен в виде суммы
всегда может быть представлен в виде суммы  , где
, где  направлен вдоль линии распространения волны, а
направлен вдоль линии распространения волны, а  лежит в плоскости, перпендикулярной этой линии. При этом для каждой компоненты
лежит в плоскости, перпендикулярной этой линии. При этом для каждой компоненты  указанных векторов справедливо волновое уравнение
указанных векторов справедливо волновое уравнение ,
, , либо поперечная
, либо поперечная  скорость звука в твердом теле.
скорость звука в твердом теле. , а волновое уравнение при учете однородности распределения всех параметров вдоль оси z можно представить в виде
, а волновое уравнение при учете однородности распределения всех параметров вдоль оси z можно представить в виде . (67)
. (67) ,
,
 решение последнего уравнения будет иметь различные типы. В частности при
решение последнего уравнения будет иметь различные типы. В частности при  , когда
, когда  , решение представляется гармоническими функциями. Это означает, что
, решение представляется гармоническими функциями. Это означает, что  описывает волну, распространяющуюся в направлении y в глубину полупространства. В противоположном случае, когда
описывает волну, распространяющуюся в направлении y в глубину полупространства. В противоположном случае, когда 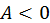 , решение последнего уравнения описывает экспоненциально затухающую в глубину полупространства зависимость:
, решение последнего уравнения описывает экспоненциально затухающую в глубину полупространства зависимость:  . Отсюда следует, что для частот, удовлетворяющих неравенству
. Отсюда следует, что для частот, удовлетворяющих неравенству  , возникает режим поверхностной волны, когда деформации и энергия волны сосредотачиваются вблизи поверхности полупространства в области с характерной толщиной
, возникает режим поверхностной волны, когда деформации и энергия волны сосредотачиваются вблизи поверхности полупространства в области с характерной толщиной  Отсюда следует, что явление поверхностной волны характерно для относительно низкочастотных колебаний. Хорошо известно, в частности, что низкочастотные составляющие колебаний земной коры, возникающие в результате землетрясений и ядерных взрывов, способны распространяться в поверхностном слое земли на многие тысячи километров.
Отсюда следует, что явление поверхностной волны характерно для относительно низкочастотных колебаний. Хорошо известно, в частности, что низкочастотные составляющие колебаний земной коры, возникающие в результате землетрясений и ядерных взрывов, способны распространяться в поверхностном слое земли на многие тысячи километров. по сравнению со скоростями распространения продольных и поперечных колебаний в неограниченном пространстве, т. е.
по сравнению со скоростями распространения продольных и поперечных колебаний в неограниченном пространстве, т. е.  На рис. 34 показано распространение упругой волны, возбуждаемой в плоском стальном массиве силой, приложенной в точке
На рис. 34 показано распространение упругой волны, возбуждаемой в плоском стальном массиве силой, приложенной в точке  и изменяющейся по закону
и изменяющейся по закону  ,
,  ,
, 




