ТЕПЛОПРОВОДНОСТЬ
Тепловые режимы и процессы в электроэнергетическом и электрофизическом оборудовании играют важную роль, определяя их рабочие характеристики и предельные возможности. Роль тепловых процессов в газоразрядных явлениях и технологиях также во многих случаях носит определяющий характер. Поэтому разделы физики, относящиеся к процессам теплопередачи, представляют для указанных инженерных областей особый интерес. Ниже будут рассмотрены классические модели теплопередачи и методы решения соответствующих задач для ряда характерных условий. Ранее мы получили уравнение энергии для сплошной среды
где ρ — массовая плотность, ε — объемная плотность внутренней энергии, P — давление, v — вектор скорости движения среды, Одним из важнейших физических механизмов теплообмена в сплошной среде является теплопроводность. Качественно на микроуровне явление теплопроводности в газах объясняется передачей энергии теплового движения частиц при столкновениях. Частицы газа, находящиеся в областях с большей температурой имеют более высокую кинетическую энергию теплового движения и при столкновениях с частицами их соседних более холодных элементов передают часть этой энергии. Таким образом, внутренняя энергия передается из более нагретой области в менее нагретую. В твердых телах, например в металлах, механизм теплопроводности реализуется в результате обмена энергией тепловых колебаний между узлами кристаллической решетки. В более нагретых областях эти колебания интенсивнее, чем в менее нагретых, однако возможность распространения колебаний в кристаллических решетках обеспечивает передачу их энергии из более нагретых областей в менее нагретые. Феноменологические свойства явления сформулированы в математической форме в начале 19 века Био и Фурье. Поток тепловой энергии или тепловой поток описывается с помощью закона Фурье
где
Как видно из формулы (69) интенсивность теплопередачи определяется не только градиентом температуры, но и средой, свойства которой выражены в коэффициенте теплопроводности
где В зависимости от знака Уравнение баланса энергии с учетом теплопроводности выведем на основе уравнения энергии (68). Без ограничения общности здесь рассмотрим малый элемент сплошной среды Скорость изменения теплосодержания
Разделив последнее уравнение на
В случае неподвижной среды v=0, и последнее уравнение примет вид
В достаточно широком интервале температур плотность внутренней энергии можно связать с температурой хорошо известным из общего курса физики линейным законом
После подстановки вместо теплового потока
В случае стационарного температурного поля последнее уравнение упрощается вследствие исчезновения производной по времени
Уравнение (71) описывает стационарное распределение температуры в пространстве с неподвижной средой. Для решения уравнения стационарной теплопроводности (71), которое является дифференциальным уравнением в частных производных, необходимы граничные условия, которые устанавливают физические законы температурного поля на границе расчетной области.
|


 — мощность источников внутренней энергии. Приведенное уравнение описывает адиабатический режим, когда элементы среды не могут обмениваться энергией друг с другом. В соответствии с этой моделью, местное выделение энергии не приводит к изменению внутренней энергии в окружающих место выделения энергии элементах среды. В случае быстро протекающих процессов элементы среды просто не успевают обмениваться тепловой энергией друг с другом, и адиабатическая модель дает адекватное описание. Однако во многих практически важных случаях обмен энергией между элементами среды становится определяющим фактором теплового режима. Поэтому нам вновь придется модифицировать уравнение энергии, чтобы учесть и явления теплообмена.
— мощность источников внутренней энергии. Приведенное уравнение описывает адиабатический режим, когда элементы среды не могут обмениваться энергией друг с другом. В соответствии с этой моделью, местное выделение энергии не приводит к изменению внутренней энергии в окружающих место выделения энергии элементах среды. В случае быстро протекающих процессов элементы среды просто не успевают обмениваться тепловой энергией друг с другом, и адиабатическая модель дает адекватное описание. Однако во многих практически важных случаях обмен энергией между элементами среды становится определяющим фактором теплового режима. Поэтому нам вновь придется модифицировать уравнение энергии, чтобы учесть и явления теплообмена.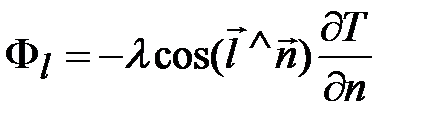 ,
, — количество тепловой энергии, передаваемой за единицу времени через единичную площадку в направлении
— количество тепловой энергии, передаваемой за единицу времени через единичную площадку в направлении  ,
,  — направление нормали к изотерме (рис. 35), коэффициент теплопроводности, являющейся индивидуальной характеристикой вещества. С помощью формул векторного анализа последнее выражение можно записать в следующем общем виде
— направление нормали к изотерме (рис. 35), коэффициент теплопроводности, являющейся индивидуальной характеристикой вещества. С помощью формул векторного анализа последнее выражение можно записать в следующем общем виде . (69)
. (69)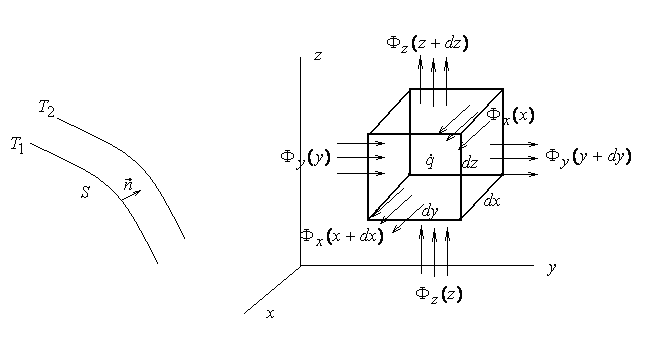 Рис. 35. К выводу уравнения теплопроводности
Рис. 35. К выводу уравнения теплопроводности
 . Теплопроводность веществ может сильно различаться. Наиболее высокой теплопроводностью обладают металлы, для которых
. Теплопроводность веществ может сильно различаться. Наиболее высокой теплопроводностью обладают металлы, для которых 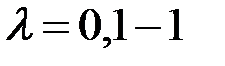 Вт/м∙ К. Наименьшей теплопроводностью обладают газы
Вт/м∙ К. Наименьшей теплопроводностью обладают газы  Вт/м∙ К. Многочисленные опыты подтверждают справедливость закон Фурье. При этом сама величина
Вт/м∙ К. Многочисленные опыты подтверждают справедливость закон Фурье. При этом сама величина 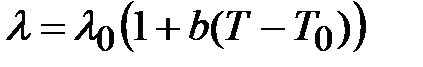 ,
, — коэффициент теплопроводности при температуре
— коэффициент теплопроводности при температуре 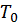 , b — постоянная, определяемая опытным путем.
, b — постоянная, определяемая опытным путем.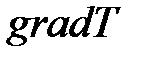 в выражении (69) тепловой поток может быть как положительным, так и отрицательным. В первом случае это приводит к уменьшению теплосодержания в данной точке, а во втором — к увеличению. Поэтому наряду с действующими в среде источниками и стоками тепловой энергии тепловой поток (69) играет равноправную роль в энергетическом балансе в некоторой точке среды.
в выражении (69) тепловой поток может быть как положительным, так и отрицательным. В первом случае это приводит к уменьшению теплосодержания в данной точке, а во втором — к увеличению. Поэтому наряду с действующими в среде источниками и стоками тепловой энергии тепловой поток (69) играет равноправную роль в энергетическом балансе в некоторой точке среды.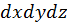 (рис. 35).
(рис. 35). выделенного элемента определяется мощностью действующего внутри него объемного источника тепловыделения
выделенного элемента определяется мощностью действующего внутри него объемного источника тепловыделения  , а также балансом входящих и выходящих через грани выделенного элемента тепловых потоков
, а также балансом входящих и выходящих через грани выделенного элемента тепловых потоков


 , где
, где 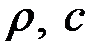 — массовая плотность и удельная теплоемкость, последнее уравнение можно переписать в виде
— массовая плотность и удельная теплоемкость, последнее уравнение можно переписать в виде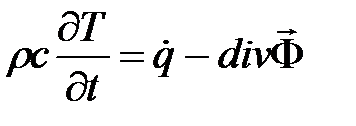 .
. его выражения через температуру (69) получим уравнение теплопроводности
его выражения через температуру (69) получим уравнение теплопроводности . (70)
. (70)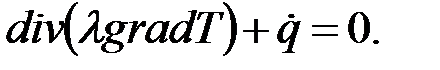 (71)
(71)


