Упражнения для самоконтроля. 1. Применима ли модель механики сплошной среды при расчете движения солнечного ветра от Солнца к Земле
1. Применима ли модель механики сплошной среды при расчете движения солнечного ветра от Солнца к Земле, если концентрация частиц в межпланетном пространстве Указания к решению задач. 1–3 — применить критериальное соотношение между размером области движения и длины свободного пробега частиц 2. В воздухе, разряженном до давления 3. Применима ли модель механики сплошной среды при расчете сопротивления движению космической межпланетной станции размером 100м в туманности с концентрацией частиц 4. Скорость течения воды в выходном отверстии воронки площадью S равна Указания к решению задачи проинтегрировать стационарное уравнение неразрывности по объему, преобразуя объемный интеграл от дивергенции в поверхностный (теорема Гаусса) 5. В бесконечном объеме несжимаемой жидкости расширяется длинная цилиндрическая полость. Определить поле скорости радиального течения вне полости, если известен закон ее расширения:
Указания к решению задачи проинтегрировать уравнение неразрывности в цилиндрической системе координат по радиусу при постоянной плотности и найти связь скорости течения в произвольной точке со скоростью на границе полости 6. В бесконечном объеме несжимаемой жидкости расширяется сферическая полость. Определить поле скоростей Указания к решению задач 6–7 — аналогично задаче 5, но с использованием сферической системы координат 7. Погруженная в идеальную несжимаемую жидкость с 8. Погруженная в идеальную несжимаемую жидкость сфера расширяется с постоянной скоростью 100 м/с. Найти разность давлений внутри и вне сферы, плотность жидкости 2 г/см3. Указания к решению задачи применить уравнение Рэлея (раздел 4.5) 9. Показать, что вдоль струи потока несжимаемой жидкости справедливо следующее выражение
где ρ — плотность, v — скорость, P — давление. Указания к решению задачи проинтегрировать стационарное уравнение течения жидкости вдоль струи 10. Определить скорость вытекания газа из полости, если давление снаружи Указания к решению задач 10-12 использовать систему уравнений Рэнкина-Гюгонио, формулы (60)-(62), ударную волну считать слабой (D=c=1450 м/с – скорость звука в воде). 11. Плита падает на воду с высоты 10 м. Рассчитать скачок воды давления в воде. Ударную волну считать слабой, то есть скорость ударной волны приблизительно равна скорости звука в воде:
12. Ударная волна движется в воздухе со скоростью 13. Рассчитать полезную мощность электродугового нагревателя плазматрона, необходимую для создания струи горячего газа сечением S, при температуре T и скорости v. Рабочий газ водород масса атома Указания к решению задачи найти ответ как полный поток кинетической и внутренней энергии газа на срезе сопла рельсотрона, использовать выражение для кинетической и внутренней энергии газа на единицу массы.
|

 см-3? Расстояние между Землей и Солнцем 149 млн.км.
см-3? Расстояние между Землей и Солнцем 149 млн.км. .
. Па при
Па при  К за время
К за время 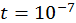 с, формируется электрический пробой. Можно ли анализировать данный процесс на стадии формирования разряда в предположении локального термодинамического равновесия? Среднюю массу молекулы для воздуха принять равной
с, формируется электрический пробой. Можно ли анализировать данный процесс на стадии формирования разряда в предположении локального термодинамического равновесия? Среднюю массу молекулы для воздуха принять равной  кг.
кг. . Найти скорость течения на входном отверстии, равном 10 S. Воду считать несжимаемой жидкостью, скорости на входном и выходном отверстиях равномерно распределены по их сечению.
. Найти скорость течения на входном отверстии, равном 10 S. Воду считать несжимаемой жидкостью, скорости на входном и выходном отверстиях равномерно распределены по их сечению.

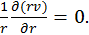
 , если известен закон изменения радиуса сферы
, если известен закон изменения радиуса сферы  .
.
 ,
,  сфера расширяется по закону
сфера расширяется по закону  . Найти закон изменения давления внутри сферы.
. Найти закон изменения давления внутри сферы.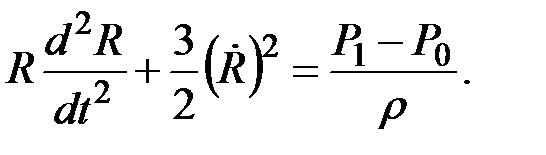

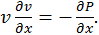
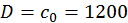 м/с.
м/с.  кг/м3.
кг/м3. (
( м/с),
м/с),  атм,
атм,  кг/м3. Найти параметры среды (P, ρ, v) за фронтом ударной волны. Считать, что за ее фронтом давление и плотность связаны законом адиабаты, коэффициент
кг/м3. Найти параметры среды (P, ρ, v) за фронтом ударной волны. Считать, что за ее фронтом давление и плотность связаны законом адиабаты, коэффициент  .
.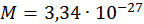 кг, плотность
кг, плотность  кг/м3, скорость
кг/м3, скорость  м/с,
м/с,  К,
К,  cм2. Температура газа на входе
cм2. Температура газа на входе  К.
К. а также выражение для полного потока массы
а также выражение для полного потока массы 



