Частотная и фазовая модуляции аналоговых сигналов. Смоделированный амплитудный манипулятор с пассивной паузой удовлетворяет поставленным требованиям
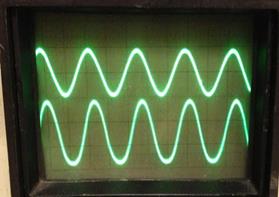
Смоделированный амплитудный манипулятор с пассивной паузой удовлетворяет поставленным требованиям. Передатчик, полученный в результате каскадного соединения автогенератора и манипулятора, работает стабильно, что видно из осциллограммы его работы. Небольшие отклонения, которые составляют не более 3%, обусловлены неточностями значений элементов при выборе в стандартной библиотеке Multisim при моделировании, и возникающими на высоких частотах паразитными емкостями и индуктивностями. Санкт-Петербургский Государственный Политехнический Университет Кафедра: ЭиЭ Лабораторная работа ИССЛЕДОВАНИЕ ЭЛЕКТРООПТИЧЕСКОГО МОДУЛЯТОРА Выполнил: студенты гр. 4027/10 Амбросович В.А. Ерин И.Е. Ефимов А.С. Коряковский А.В. Сыропятов Д.А.
Проверил:_________ Г Цель работы: Ознакомиться с устройством, принципом действия и характеристиками электрооптического модулятора (ЭОМ) на основе эффекта Поккельса. Описание лабораторной установки: Лабораторная установка включает в себя маломощный гелий-неоновый лазер (l = 633 нм) с вертикальной линейной поляризацией излучения (рис. 4.2). Лазер укреплен на оптической скамье соосно с ЭОМ и фотоприемником. ЭОМ выполнен на основе кристалла КДР. В качестве анализатора используется пленочный поляроид призма. Крепление анализатора в модуляторе обеспечивает его вращение вокруг оси лазерного пучка на 360°.
Рис. 1. Структурная схема лабораторной установки
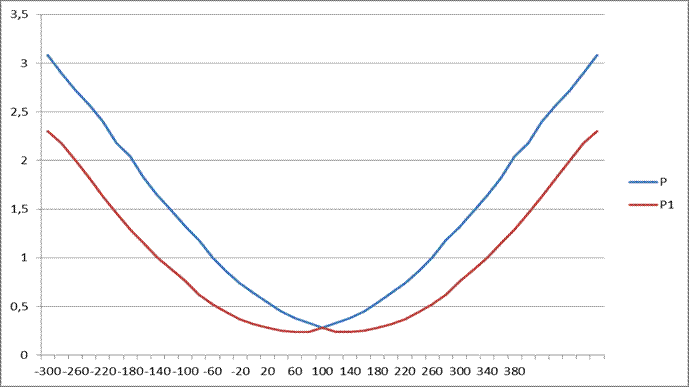
Область прозрачности модулятора 350...1200 нм. Напряжение полного просветления на длине волны 633 нм не более 700 В; потери света в режиме полного просветления – не более 30%; остаточный уровень светового потока в режиме полного затемнения – не более 7%. Диапазон частот модуляции 0.01...100 МГц. Кристалл КДР снабжен электродами, благодаря которым создается поперечное электрическое поле по отношению к направлению распространения лазерного пучка. Использование продольного электрического поля улучшает частотные свойства ЭОМ за счет уменьшения паразитной межэлектродной емкости, но требует существенного повышения напряжения смещения. Регулируемое напряжение смещения подается на кристалл от стабилизированного источника питания. Для расширения диапазона исследования в источнике предусмотрена смена полярности напряжения смещения. Модулирующий синусоидальный сигнал поступает на вход ЭОМ от генератора. Выход фотоприемника соединен с цифровым вольтметром, контролирующим сигнал, пропорциональный постоянной составляющей мощности излучения P t, прошедшей модулятор. Переменная составляющая сигнала излучения Р m регистрируется с помощью двухлучевого осциллографа, имеющего калиброванные входы. На второй вход осциллографа подается опорный сигнал от генератора. Экспериментальные данные: Зависимость пропускания ЭОМ от угла поворота анализатора:
Зависимость пропускания ЭОМ от напряжения на ЭОМ, при минимальном угле пропускания (80˚):
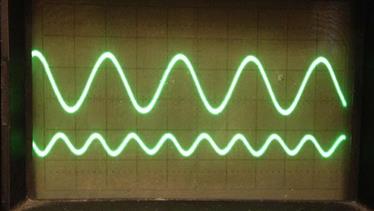
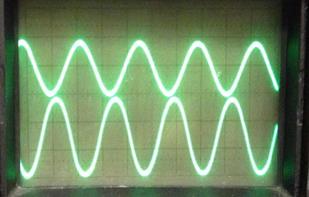
Осциллограммы опорного сигнала и переменной составляющей мощности излучения Р m для различных режимов:
Удвоение частоты (U = 40 В, f = 21 Гц):
Режим искажения амплитуды для разных полярностей:
Выводы: На основе газового разряда существует много приборов, гелий-неоновые лазеры, у которых все процессы происходят на тлеющем разряде. Также есть лазерное излучение, на него можно воздействовать ЭОМ или анализатором. При распространении линейно поляризованного излучения лазера с длиной волны l и мощностью P 0 вдоль геометрической оси z двулучепреломляющего кристалла происходит его разложение на взаимно перпендикулярно поляризованные “обыкновенный” и “необыкновенный” лучи, показатели преломления n о и nе для которых различны, причем n е больше nо. В результате “обыкновенный” луч распространяется быстрее “необыкновенного”, что после прохождения кристалла протяженностью l приводит к сдвигу фаз между лучами Dj = 2p(nе – nо) l /l. Частотная и фазовая модуляции аналоговых сигналов. Поскольку мгновенная частота
то частотная и фазовая модуляция взаимозависимы, их объединяют даже общим названием - угловая модуляция. При частотной модуляции (ЧМ) мгновенная частота сигнала изменяется по закону модулирующего сигнала, при фазовой (ФМ) - фаза. Поэтому при модуляции тестовым синусоидальным сигналом частотой
при ЧМ и ФМ соответственно получим:
где
где Высокочастотное, несущее колебание:
При частоте модуляции тональных сигналов (2) с учетом (3) несущее колебание (5) примет вид:
где индекс При фазовой модуляции тональный сигнал (2) с учетом (4) несущее колебание (5) примет вид:
где Из (6) и (7) следует, что при частоте модулирующего сигнала При ФМ согласно (7) амплитуда колебания фазы сигнала
и, следовательно, девиация частоты пропорциональна частоте модулирующего сигнала
Рисунок 1 – Частотная и фазовая модуляции
Таким образом, при обеих видах угловой модуляции - ЧМ и ФМ -меняется как мгновенная частота, так и фаза модулируемого высокочастотного сигнала. Однако, два основных параметра, характеризующих эти виды модуляции - девиация частоты Спектр сигнала при частотной и фазовоймодуляции. Обратимся к выражению для ЧМ-сигнала (6), представив его в виде суммы двух слагаемых:
Разложив в периодические функции в (9) в ряд Фурье, имеем:
где Согласно (10) при ЧМ спектр высокочастотного сигнала при тональном модулирующем сигнале частотой Пакет программ «Mathcad» представляет возможность путем обращения к функции J0,J1,Jn вычислить значения бесселевой„функции 1-го рода n-порядка при любом значении аргумента mЧ. Такая программа и графики бесселевой функции при n=0…8 и mЧ=0…20 приведены на рисунке 2. С помощью данных графиков можно построить спектр ЧМ и ФМ сигнала при заданном значении mЧ=х или
Рисунок 2– Спектральная составляющая
Следует заметить, что спектральная составляющая с частотой Теоретически спектр ЧМ-сигнала безграничен. Однако, как показывает аналез, большая часть энергии ЧМ-сигнала сосредоточена в полосе:
где F- высшая частота в спектре модулирующего сигнала. Именно на эту величину и следует рассчитывать полосы пропускания высокочастотных трактов радиопередатчиков и радиоприемников. При mч <<2-3- широкополосный. Преимущества частотной модуляции в полной мере реализуются при mч >1.
|

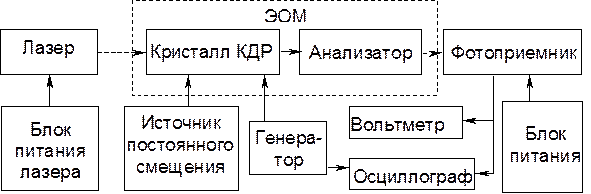

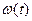 с фазой
с фазой  сигнала связана соотношением
сигнала связана соотношением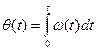 , (1)
, (1) :
: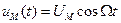 , (2)
, (2)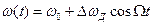 , (3)
, (3) - девиация частоты;
- девиация частоты;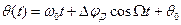 , (4)
, (4) - девиация фазы.
- девиация фазы. (5)
(5) , (6)
, (6) - частотная модуляция.
- частотная модуляция.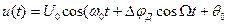 , (7)
, (7) - девиация фазы или индекс фазовой модуляции.
- девиация фазы или индекс фазовой модуляции. отличить частотную модуляцию от фазовой не представляется возможным. Это различие можно обнаружить только при изменении частоты
отличить частотную модуляцию от фазовой не представляется возможным. Это различие можно обнаружить только при изменении частоты  при изменении частоты
при изменении частоты 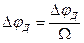 .
. , а мгновенная частота сигнала меняется по закону:
, а мгновенная частота сигнала меняется по закону: (8)
(8) . Данное различие между ЧМ и ФМ иллюстрируется с помощью графиков, построенных на рисунке.1
. Данное различие между ЧМ и ФМ иллюстрируется с помощью графиков, построенных на рисунке.1
 и девиация фазы
и девиация фазы 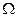 .
. (9)
(9)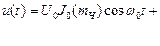

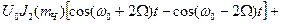 (10)
(10) ,
,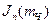 - бесселева функция 1-го рода n-порядка от аргумента mЧ.
- бесселева функция 1-го рода n-порядка от аргумента mЧ. , а амплитуды и
, а амплитуды и  . Аналогичный результат получается и при фазовой модуляции с заменой параметра mЧ на
. Аналогичный результат получается и при фазовой модуляции с заменой параметра mЧ на 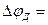 х. В качестве примера такие спектрограммы при mЧ=5 и 2,4 приведены на рисунке 2
х. В качестве примера такие спектрограммы при mЧ=5 и 2,4 приведены на рисунке 2
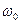 и несущая частотой
и несущая частотой  (11)
(11)


