ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
Пусть · потенциал обкладки конденсатора, на которой находится заряд · а потенциал обкладки, на которой находится заряд Энергия такой системы зарядов равна:
то есть равна собственной энергии системы зарядов, где Найдем энергию 1. плоского конденсатора. Энергия, заключенная в единице объема электростатического поля называется объемной плоскостью энергии. Эта объемная плоскость должна быть одинаковой во всех точках однородного поля, а полная энергия поля пропорциональна его объему. Известно, что тогда для энергии имеем: но то есть Тогда объемная плотность энергии то есть определяется его напряженностью или смещением. В случае неоднородных электрических полей 2. сферического конденсатора. На расстоянии Рассмотрим бесконечно тонкий шаровой слой, заключенный между сферами радиусов Объем такого слоя: Энергия слоя следовательно Тогда полная энергия заряженного шара равна: Но емкость шара следовательно,
|

 , равен
, равен 
 ,
,  .
. ,
,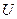 - напряжение между обкладками конденсатора,
- напряжение между обкладками конденсатора,  .
. ,
,  ,
, ,
, - объем электростатического поля между обкладками конденсатора,
- объем электростатического поля между обкладками конденсатора, .
. однородного электростатического поля конденсатора равна
однородного электростатического поля конденсатора равна  ,
, .
. от центра заряженного шара напряженность его электростатического поля равна
от центра заряженного шара напряженность его электростатического поля равна  .
.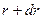 .
. .
.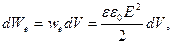 ,
, .
. , где
, где 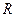 - радиус шара.
- радиус шара.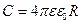 ,
, - энергия электростатического поля сферического конденсатора равна его собственной энергии, так как заряженное тело потому и обладает электрической энергией, что при его зарядке была совершена работа против сил создаваемого им электростатического поля.
- энергия электростатического поля сферического конденсатора равна его собственной энергии, так как заряженное тело потому и обладает электрической энергией, что при его зарядке была совершена работа против сил создаваемого им электростатического поля.


