ЭЛЕКТРОЕМКОСТЬ УЕДИНЕННОГО ПРОВОДНИКА
Рассмотрим проводник, находящийся в однородной среде вдали от других проводников. Такой проводник называется уединенным. При сообщении этому проводнику электричества, происходит перераспределение его зарядов. Характер этого распределения зависит от формы проводника. Каждая новая часть зарядов распределяется по поверхности проводника подобно предыдущей, таким образом, при увеличении в где Разобьем поверхность проводника · Потенциал
· Потенциал в произвольной точке электростатического поля, образованного замкнутой поверхностью проводника, равен интегралу:
Для точки, лежащей на поверхности проводника, В этом случае интеграл зависит только от размеров и формы поверхности При этом для всех точек проводника потенциал одинаков, поэтому и значения Считается, что потенциал незаряженного уединенного проводника равен нулю. Из формулы (1) видно, что потенциал уединенного проводника прямо пропорционален его заряду. Отношение Электроемкость уединенного проводника численно равна электрическому заряду, который нужно сообщить этому проводнику для того, чтобы потенциал проводника изменился на единицу. Электроемкость проводника зависит от его формы и размеров, причем геометрически подобные проводники обладают пропорциональными емкостями, так как распределение зарядов на них также подобно, а расстояния от аналогичных зарядов до соответствующих точек поля прямо пропорциональны линейным размерам проводников. Потенциал ж е электростатического поля, создаваемого каждым точечным зарядом, обратно пропорционален расстоянию от этого заряда. Таким образом, потенциалы одинаково заряженных и геометрически подобных проводников изменяются обратно пропорционально их линейным размерам, а емкости этих проводников – прямо пропорционально.
|

 раз заряда
раз заряда  проводника во столько же раз возрастает
проводника во столько же раз возрастает  в любой точке его поверхности, то есть
в любой точке его поверхности, то есть  ,
, - некоторая функция координат рассматриваемой точки поверхности.
- некоторая функция координат рассматриваемой точки поверхности. на бесконечно малые элементы
на бесконечно малые элементы  , заряд каждого такого элемента равен
, заряд каждого такого элемента равен  , и его можно считать точечным.
, и его можно считать точечным. поля заряда
поля заряда  равен:
равен:
 (1)
(1) одинаковы.
одинаковы. называется электрической емкостью
называется электрической емкостью 
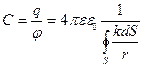 (2)
(2)


