Проекции плоских кривых линий

 

1. Фамилия, имя, отчество практиканта.

2. Где, в какой должности и под чьим руководством проходил практику.

3. Отношение практиканта к работе (интерес, инициатива, оперативность,

исполнительность, соблюдение трудовой дисциплины, деловитость).

4. Качество выполняемой практикантом работы.

5. Степень овладения практическими умениями и навыками по направлению подготовки.

6. Личные качества практиканта.

7. Недостатки в работе и теоретической подготовке.

8. На какой самостоятельной работе он может быть использован по окончании университета.

 

 

Подпись руководителя практики от организации (предприятия)

 

Проекции плоских кривых линий

 

При построении проекций плоской кривой линии необходимо указывать на их так называемые характерные точки, к которым относятся особые точки кривой, а также точки, наиболее удаленные от плоскостей проекций и наиболее близкие к ним.

Обыкновенной точкой кривой называют такую точку М (рисунок 4.3), которую можно заключить в прямоугольник (хотя бы очень малый) так, что попавшая внутрь него часть кривой является простым отрезком*.

Все другие точки называются особыми** (А и В на рисунок 4.3).

 

 

Рисунок 4.3

 

На рисунок 4.3 изображены некоторые из особых точек плоских кривых:

1) узловая точка А или точка самопересечения (рисунок 4.4, а), в которой кривая имеет две различные касательные;

2) точка возврата первого рода (рисунок 4.4, б), в которой кривая подходит к точке двумя ветвями, имеющими в точке В общую касательную и расположенными по разные стороны от касательной;

3) точка возврата второго рода С (рисунок 4.4, в), в которой кривая подходит к точке двумя ветвями, имеющими в точке С общую касательную, расположенную (вблизи точки С) по одну сторону от обеих ветвей кривой.

 

а)	б)	в)

 

Рисунок 4.4

 

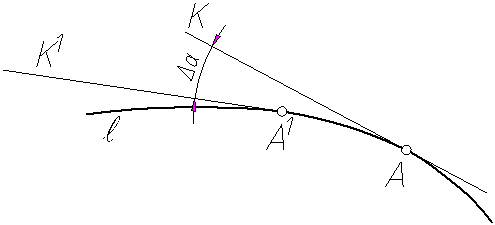
Характерным признаком линии является ее кривизна. Кривизной х линии l (рисунок 4.5) в данной ее точке А называется предел, к которому стремится отношение угла смежности Da между касательными k и k' в точках А и А¢ к дуге АА¢ =ΔS, когда точка А¢ оставаясь на линии l, стремится к А.

х = lim / s при s 0.

 

Из этого определения следует, что кривизна прямой во всех ее точках равна нулю, а кривизна окружности данного радиуса - величина постоянная.

 

 

Рисунок 4.5

 

Элементы кривой линии

 

Выделяют циркульные и лекальные кривые. Циркульные кривые имеют постоянную кривизну. У лекальных кривых кривизна непрерывно меняется по длине кривой.

* Простым отрезком кривой называется множество точек, координаты которых хотя бы в одной прямоугольной декартовой системе удовлетворяют уравнению y= f (x) при x₁<x<x₂ где x₁ и х₂ - два фиксированных значения, a f (x₁) предполагается однозначной, непрерывной и достаточное число раз дифференцируемой.

** Особые точки рассматриваются в курсе дифференциальной геометрии.