Минимизация по правильному симплексуПравильным симплексом в пространстве En называется множество из п + 1 равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса. В пространстве E2 правильным симплексом является совокупность вершин равностороннего треугольника, в E3 – правильного тетраэдра. Шаг 0. Выбрать параметр точности e, базовую точку х0, ребро a и построить начальный симплекс по формулам Шаг 1. Вычислить значения f (х) в вершинах симплекса х1,.., xn. Шаг 2. Упорядочить вершины симплекса х0,.., хn так, что бы f (х0) £ …£ £f (х1) £ f (хn–1) £ f (хn). Шаг 3. Проверить условие
Если оно выполнено, то вычисления прекратить, полагая х*» х0, f *» f (x0). В противном случае перейти к шагу 4. Шаг 4. Найти
Шаг 5. Найти Шаг 6. Перейти к новому правильному симплексу с вдвое меньшим ребром, считая базовой вершиной х0. Остальные п вершин симплекса найти по формуле хi = (хi + х0)/2, i=1,.., п. Перейти к шагу 1. Геометрическая иллюстрация работы алгоритма в пространстве показана на рис., где точки х0, х1, х2 – вершины начального симплекса, а пунктиром указаны процедуры отражения.
|
где d1 
, d2 
, a– длина ребра.. Вычислить f (х0).
(3.38)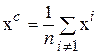
и выполнить отражение вершины хn:
=2xc – хn.Если f (
) <f (xn), то положить хn= 
и перейти к шагу 2. Иначе – перейти к шагу 5.
и выполнить отражение вершины хn–1: 
= 2x c – хn–1. Если f (
) < f (хn–1), то положить хn–1 = 
