Первый метод деления отрезка пополам (дихотомии).
Шаг 1. Определить x1 и х2 по формулам Шаг 2. Сравнить f (x1) и f (x2). Если Шаг 3. Найти достигнутую точность Шаг 4. Положить Метод золотого сечения. Шаг 1. Найти х1 и х2 по формулам Шаг 2. Проверка на окончание поиска: если en > e, то перейти к шагу 3, иначе – к шагу 4. Шаг 3. Переход к новому отрезку и новым пробным точкам. Если f (x1) £ f (x2) то положить b=x2, x2=x1, f (x2) £ f (x1), x1=b–t(b–a) и вычислить f (x1), иначе – положить a=x1, x1= x2, f (x1) = f (x2), x2=b+t(b–a) и вычислить f (x2). Положить en = ten и перейти к шагу 2. Шаг 4. Окончание поиска: положить Метод парабол Шаг 1. Выбрать точки x1, x2, x3, удовлетворяющие условиям х1 < х2 < х3, f (x1) ³ f (x2) £ f (x3). Перейти к шагу 2.
Шаг 2. Найти
Шаг 3. Проверка на окончание поиска. Сравнить модуль разности значений Шаг 4. Вычислить значение f ( Шаг 5. Определить новую тройку чисел x1, x2, x3. Присвоить f (x1), f (x2) и f (x3) соответствующие значения f (x) найденные ранее. Перейти к шагу 2.
|

 , где d > 0 – малое число.. Вычислить f (x1) и f (x2).
, где d > 0 – малое число.. Вычислить f (x1) и f (x2). , то перейти к отрезку [а; x2], положив b = x2, иначе – к отрезку [x1; b], положив а = x1.
, то перейти к отрезку [а; x2], положив b = x2, иначе – к отрезку [x1; b], положив а = x1.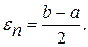 Если
Если  , то перейти к следующей итерации, вернувшись к шагу 1. Если
, то перейти к следующей итерации, вернувшись к шагу 1. Если  , то завершить поиск х*, перейдя к шагу 4.
, то завершить поиск х*, перейдя к шагу 4.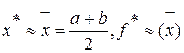 .
.
 . Вычислить f (x1) и f (x2). Положить
. Вычислить f (x1) и f (x2). Положить  ,
,  .
. ,
,  .
. по формуле
по формуле  . На первой итерации перейти к шагу 4, на остальных – к шагу 3.
. На первой итерации перейти к шагу 4, на остальных – к шагу 3.


