Алгоритм выполнения работы

 

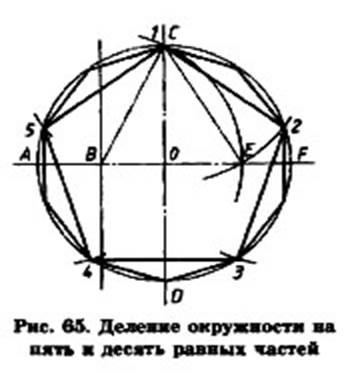
1 Через центр окружности О провести два взаимноперпендикулярных диаметра АF и СD.

2 Разделить отрезок AO пополам, получим точку B.

3 Из точки B провести дугу радиусом BС, получим точку E пересечения с диаметром АF.

4 Соединить точки С и E, получим отрезок СE, размер которого делит окружность на пять равных частей.

5 Из точки С сделать засечки на заданной окружности длиной, равной отрезку СE. Полученные точки пересечении делят окружность на пять равных частей (рисунок 9).

 

Рисунок 9 – Деление окружности на пять равных частей

Задание: Дано: окружность радиусом R = 20мм.

Требуется разделить заданную окружность на пять равных частей.

Ход работы

 

Упражнение 4 Касательные

Упражнение выполняется в рабочей тетради.

Построение прямой линии, проходящей через заданную точку и касательной к заданной окружности.

Алгоритм выполнения работы

1 Соединить точку А с центром окружности О, получим отрезок ОА.

2 Разделить отрезок ОА пополам, получим точку О₁, являющуюся центром дополнительной окружности.

3 Построить дополнительную окружность радиусом R₁, равным отрезку О₁А, получим точки пересечения m и n заданной окружности и вспомогательной. Данные точки будут точками сопряжения, а линии А m и А n – касательными к данной окружности (рисунок 10).

 

Рисунок 10 - Построение прямой линии, проходящей через заданную точку и касательной к заданной окружности

Задание:Дано: точка К и окружность радиусом R = 15 мм.

Требуется в рабочей тетради построить прямую линию, проходящую через заданную точку К и касательной к заданной окружности.