Проводники в электрическом поле.
Проводники в электрическом поле. Проводники. Наиболее хорошими проводниками электричества являются металлы. Основные особенности проводников состоят в следующем: 1) В проводниках имеются свободные заряды, т.е. индуцированные заряды разделяются (могут быть разделены механически); в металлах свободными зарядами являются электроны. 2) В равновесном состоянии электрическое поле внутри проводника, находящегося во внешнем поле или заряженного до некоторого значения В противном случае на электрические заряды в проводнике будет действовать со стороны поля сила, приводящая их в движение и вызывающая перераспределение зарядов. В электростатическом состоянии движение зарядов отсутствует, откуда следует, что электрическое поле внутри проводящего вещества должно быть равно нулю. Отсюда неизбежно получаем, что в стационарном состоянии в проводнике
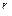 избыточных (нескомпенсированных) зарядов внутри однородного проводника также равна нулю. избыточных (нескомпенсированных) зарядов внутри однородного проводника также равна нулю.
Заметим, что мы имеем в виду поле, усредненное по объему, который велик по сравнению с характерными объёмами атомов. 3) Избыточный электрический заряд может располагаться только на поверхности проводника с некоторой плотностью 4) Отсутствие поля внутри проводника (
 внутри и вне проводника должна быть равна нулю. внутри и вне проводника должна быть равна нулю.
6) Поле вблизи поверхности проводника. Пусть интересующий нас участок поверхности проводника граничит с вакуумом (
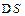 с плотностью стороннего заряда с плотностью стороннего заряда 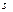 , можем записать , можем записать
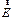 (из-за (из-за 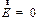 внутри проводника и внутри проводника и  ) равен нулю. То ) равен нулю. То
Емкость проводников. Если проводнику сообщить заряд Итак, рассмотрим уединенный заряженный проводник. Если увеличить его заряд на
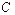 называют электроемкостью или емкостью уединенного проводника. называют электроемкостью или емкостью уединенного проводника.
Емкость зависит от размеров и формы проводника. Она численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. Пример: Пусть проводящий уединенный шар имеет радиус
 и единица емкости 1 Фарада: и единица емкости 1 Фарада:
Фарада - очень большая величина, так
Конденсаторы. Наличие вблизи проводника других тел изменяет его электрическую емкость, т.к. потенциал проводника зависит и от электрических полей, создаваемых зарядами, наведенными в окружающих телах вследствие электростатической индукции. При приближении к заряженному проводнику других тел в них будет происходить перераспределение зарядов, причем так, что ближе окажутся заряды противоположные по знаку заряду рассматриваемого проводника. Поэтому потенциал проводника, являющийся алгебраической суммой потенциалов собственных и индуцированных на других телах зарядов, уменьшится, а, значит, его емкость увеличится. Конденсатором называют систему, состоящую из двух проводников, отделенных слоем диэлектрика, расстояние между которыми много меньше их линейных размеров. Чтобы внешние поля не оказывали заметного влияния на емкость конденсатора, нужно, чтобы поле, создаваемое накапливающимися на обкладках зарядами, было практически полностью сосредоточено внутри конденсатора. В реальном конденсаторе это условие выполняется приближенно, но с достаточно хорошей точностью. Заряд конденсатора (заряд, расположенный на одной из его обкладок), связан с разностью потенциалов между обкладками конденсатора через коэффициент пропорциональности - емкость конденсатора:
1). Плоский конденсатор: две параллельные проводящие пластинки, между которыми расположен тонкий диэлектрик с диэлектрической проницаемостью
Отсюда находим связь между напряжением на конденсаторе и его электрическим полем:
.
3). Цилиндрический конденсатор: обкладками конденсатора служат два проводящих коаксиальных цилиндра радиусами
где
Параллельное и последовательное соединение конденсаторов (СРС).
|

 , равно нулю (
, равно нулю (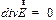
 , т.е. проводник представляет собой эквипотенциальную область пространства, а его поверхность – эквипотенциальную поверхность.
, т.е. проводник представляет собой эквипотенциальную область пространства, а его поверхность – эквипотенциальную поверхность.
 ), т.е.
), т.е.  .
.
 ).
).

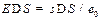

 , то он распределится аналогичным образом, лишь возрастет напряженность поля вблизи поверхности и потенциал проводника. Опыт показывает, что между зарядом проводника и его потенциалом существует прямая пропорциональность (потенциал на бесконечности считаем равным нулю):
, то он распределится аналогичным образом, лишь возрастет напряженность поля вблизи поверхности и потенциал проводника. Опыт показывает, что между зарядом проводника и его потенциалом существует прямая пропорциональность (потенциал на бесконечности считаем равным нулю):
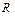 . Найдем потенциал этого шара
. Найдем потенциал этого шара
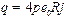
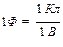 .
. - это емкость шара радиусом 9×109 м, что в 1500 раз больше радиуса Земли (емкость Земли
- это емкость шара радиусом 9×109 м, что в 1500 раз больше радиуса Земли (емкость Земли  ). Поэтому для практических нужд вводят обычно кратные величины:
). Поэтому для практических нужд вводят обычно кратные величины:  .
.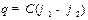

 . Расстояние между пластинами равно
. Расстояние между пластинами равно  , площадь пластин равна
, площадь пластин равна 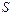 . Напряжение на конденсаторе определяется как
. Напряжение на конденсаторе определяется как
 .
.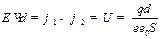


 и
и  (обкладки конденсатора), разделенные тонким слоем диэлектрика с диэлектрической проницаемостью
(обкладки конденсатора), разделенные тонким слоем диэлектрика с диэлектрической проницаемостью 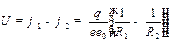 ,
,

 и
и  , между которыми расположен тонкий диэлектрик с диэлектрической проницаемостью
, между которыми расположен тонкий диэлектрик с диэлектрической проницаемостью  (при этом
(при этом  ). Поле внутри цилиндрического конденсатора (между цилиндрами) легко найти, используя теорему Гаусса:
). Поле внутри цилиндрического конденсатора (между цилиндрами) легко найти, используя теорему Гаусса: ,
, заряд, приходящийся на единицу длины одного из цилиндров. Тогда разность потенциалов между обкладками цилиндрического конденсатора:
заряд, приходящийся на единицу длины одного из цилиндров. Тогда разность потенциалов между обкладками цилиндрического конденсатора: .
.
 .
.


