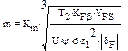Геометрия зубчатых передач
Поверхности взаимодействующих зубьев должны обеспечивать постоянство передаточного числа. Основная теорема зацепления: общая нормаль, проведенная через точку касания профилей, делит расстояние между центрами зубчатых колес на части, обратно пропорциональные угловым скоростям.
зависимости от модуля m числа зубьев z:
Зная определяют число зубьев шестерни
21. Расчетная нагрузка
22. Расчет на контактную прочность зубчатых передач Целью расчета является предотвращение усталостного выкрашивания.
Расчет производится по формуле Герца-Беляева. Зависимость Герца-Беляева для нормальных напряжений в месте контакта двух сухих неподвижных цилиндров из изотропных материалов
qH – удельная погонная сила по нормали к профилю; n1, n2 – коэффициент пуансона; E1, E2 – модуль упругости материала, r – радиусы кривизны каждого цилиндра. 1/r=1/r1 ± 1/r2, «+» для внешного зацепления, «–» для внутренного зацепления. Формула Герца-Беляева для пары зубчатых колес
ZE – коэффициент, учитывающий свойства материалов
Ze – коэффициент, учитывающий суммарную длину контактных линий
23. Контактные напряжения и контактная прочность
частиц
24. Расчет зубчатых передач на изгиб Расчет выполняется при предположениях, что зуб нагружен силой FH, в зацеплении находится одна пара зубьев, а также силы трения отсутствуют.
Наибольшее трение в точке b, однако растягивающий эффект в точке a, r – радиус выпуклости зуба,
YFS – коэффициент, учитывающий форму зуба и концентрацию напряжения Yb – коэффициент, учитывающий угол наклона Ye – коэффициент, учитывающий перекрытие зубьев. Ye= 1/e£ – для косозубой передачи, Ye = 1 для прямозубой передачи. m выбрать по возможности меньше, z соответственно больше. m=(0,01... 0,02)aW. В случае открытой передачи
|


 - угол зацепления;
- угол зацепления; 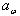 - межосевое расстояние; d1, d2 - диаметры делительных окружностей;
- межосевое расстояние; d1, d2 - диаметры делительных окружностей;  - высота головки и ножки зуба;
- высота головки и ножки зуба; 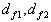 - диаметры окружностей впадин,
- диаметры окружностей впадин,  - диаметры окружностей выступов. Основной параметр зубчатых колес – модуль m:
- диаметры окружностей выступов. Основной параметр зубчатых колес – модуль m: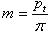

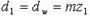 ,
, 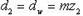

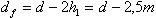

 - суммарное число зубьев.
- суммарное число зубьев.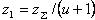 и колёса
и колёса 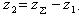 .
.
 - коэффициент ширины венца колеса.
- коэффициент ширины венца колеса.
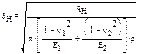
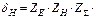
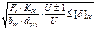

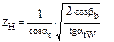
 – для прямозуб.
– для прямозуб. – для косозубых
– для косозубых



 £[d]F
£[d]F