Геометрические свойства эллипса (исследование канонического уравнения).
Свойство 10. Т очки пересечения эллипса, заданного уравнением (4), с осями координат: 1) с осью абсцисс: Получили точки А 1(– а; 0), А 2(а; 0). 2) с осью ординат: Получили точки В 1(0; – b), В 2(0; b). Точки А 1, А 2, В 1, В 2 называются вершинами эллипса. Отрезок А 1 А 2= 2а называется большой осью, отрезок В 1 В 2=2 b – малой осью. Величины а и b называются соответственно большой и малой полуосями. 3) Эллипс не проходит через точку О, т.к. Свойство 20. Оси координат являются осями симметрии эллипса, заданного уравнением (13.4), Так как уравнение содержит только квадраты текущих координат, т.е. если М (х; у) – точка эллипса, то точки М 1(– х; у), М 2(х;– у) также принадлежат ему. Ось симметрии, на которой располагаются фокусы, называется фокальной. Точка О – точка пересечения осей симметрии – является центром симметрии, так как уравнению (13.4) удовлетворяют координаты точки М 3(– х;– у). Центр симметрии называется центром эллипса. Свойство 30. Из уравнения (13.4) следует, что Это значит, что: эллипс заключен в прямоугольнике, ограниченном прямыми
Свойство 40. Если в (13.4) а=b, то получим Свойство 50. Рассмотрим точку М (х; у) эллипса, лежащую в первой координатной четверти. Из уравнения (4) для нее следует:
Очевидно, что при возрастании значения х от 0 до а значение у убывает от b до 0. Аналогично во второй четверти: при возрастании значения х от – а до 0 значение у возрастает от 0 до b, третьей: при возрастании значения х от – а до 0 значение у убывает от 0 до – b, четвертой: при возрастании значения х от 0 до а значение у возрастает от – b до 0. Свойство 60. Из (13.5) следует, что форма эллипса зависит от отношения полуосей Свойство 70. Для любой точки, принадлежащей эллипсу, r 1+ r 2 = 2 а, для любой точки, лежащей внутри эллипса r 1+ r 2<2 а, для любой точки, лежащей вне эллипса r 1+ r 2>2 а.
|

 , отсюда
, отсюда 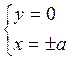 .
. , отсюда
, отсюда  .
. .
. ,
,  , откуда
, откуда  ,
, 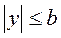 или
или  ,
, 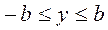 .
. ,
, 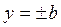 .
.
 , т.е. эллипс представляет собой окружность с центром в точке О радиусом а, тогда из (13.3): F 1 F 2= с =0, т.е. F 1= F 2 (фокусы совпадают).
, т.е. эллипс представляет собой окружность с центром в точке О радиусом а, тогда из (13.3): F 1 F 2= с =0, т.е. F 1= F 2 (фокусы совпадают). (13.5).
(13.5). : чем больше b, тем эллипс менее сжат к оси абсцисс, и наоборот.
: чем больше b, тем эллипс менее сжат к оси абсцисс, и наоборот.


