Вывод канонического уравнения эллипса
ЭЛЛИПС
Определение 1. Эллипсом называется геометрическое место точек плоскости, от каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Вывод канонического уравнения эллипса Введем обозначения: F 1 и F 2 – фокусы, сумма расстояний F 2 М+F 1 М =2 а, F 1 F 2=2 с – фокусное расстояние, причем по опр-ю 2 а >2 с или а > с. F 1 М 0 =r 1и F 2 М 0= r 2 – левый и правый фокальные радиусы точки М 0.
Введем прямоугольную систему координат. Пусть ось Ох проходит через точки F 1 и F 2, как показано на рисунке (положительное направление от F 1 к F 2); начало координат О – середина отрезка F 1 F 2. Тогда координаты точек: F 1(– с; 0) и F 2(с; 0).
Пусть М (х; у) – произвольная точка плоскости, для которой справедливо: F 1 М+F 2 М =2 а (13.1).
Запишем условие (1) в координатах:
Это уравнение эллипса в выбранной прямоугольной системе координат. Выполним тождественные преобразования:
Разделим обе части равенства на (а 2– с 2), получим:
По условию а > с, тогда разность а 2– с 2 – величина положительная, ее принято обозначать b2, т.е. b 2 =а 2– с 2 (13.3) Тогда
Определение 2. Уравнение (13.4) называется каноническим уравнением эллипса.
Очевидно, что эллипс – линия второго порядка. 2. Покажем, что всякая точка, координаты которой удовлетворяют уравнению (13.4), принадлежит эллипсу (по определению). Пусть М 0(х 0; у 0) – точка, координаты которой удовлетворяют уравнению (13.4), т.е.
Отсюда
Найдем расстояния r 1 =F 1 М 0 и r 2= F 2 М 0. r 1 =
аналогично r 2 = (Из условия (13.3): а > с, из уравнения (13.4): Значит, а > r 1+ r 2 =F 1 М 0 +F 2 М 0=
Точка М 0 принадлежит эллипсу по определению.
|



 и F 2 М=
и F 2 М=  ,
, . (13.2)
. (13.2) ,
, ,
, ,
, ,
,
 ,
, .
. .
. (13.4)
(13.4) .
. .
.


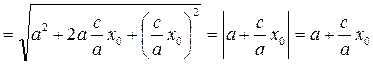 ;
;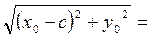
 .
. , т.е.
, т.е.  .
.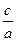 х 0.
х 0.
 =2 а.
=2 а.


