Урок №36. Задачи с уравнением окружности
Вспомним сначала общее уравнение окружности с центром 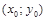 и радиусом
и радиусом  :
: 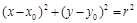 . Понятно ли, почему оно именно такое? Слева записан квадрат расстояния от точки
. Понятно ли, почему оно именно такое? Слева записан квадрат расстояния от точки 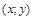 до точки
до точки 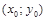 , он должен быть равен квадрату радиуса. Потренируемся в изображении окружностей.
, он должен быть равен квадрату радиуса. Потренируемся в изображении окружностей.
1. 
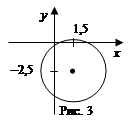 Изобразить на плоскости следующие окружности: а)
Изобразить на плоскости следующие окружности: а) 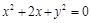 ; б)
; б)  ; в)
; в) 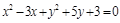 . Решение. а) Нужно сформировать в левой части полные квадраты:
. Решение. а) Нужно сформировать в левой части полные квадраты: 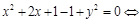
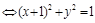 . Итак, мы получили окружность с центром в точке (–1; 0) радиуса 1 (рис. 1). б) Сформировав полные квадраты, получим уравнение
. Итак, мы получили окружность с центром в точке (–1; 0) радиуса 1 (рис. 1). б) Сформировав полные квадраты, получим уравнение 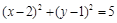 . Это окружность с центром в точке (2; 1) и радиусом
. Это окружность с центром в точке (2; 1) и радиусом 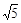 (рис. 2). Чтобы точнее изобразить эту окружность, заметим, что она проходит через начало координат: это видно из уравнения. в) Получим уравнение
(рис. 2). Чтобы точнее изобразить эту окружность, заметим, что она проходит через начало координат: это видно из уравнения. в) Получим уравнение  (рис. 3).
(рис. 3).
2.  Найти площадь фигуры, заданной неравенствами
Найти площадь фигуры, заданной неравенствами 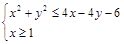 . Решение. Изобразим множество точек, удовлетворяющих первому неравенству. Для этого перепишем его в таком виде:
. Решение. Изобразим множество точек, удовлетворяющих первому неравенству. Для этого перепишем его в таком виде: 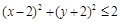 . Граница этого множества — окружность
. Граница этого множества — окружность 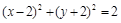 с центром в точке
с центром в точке  и радиусом
и радиусом 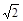 . Неравенству
. Неравенству 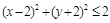 удовлетворяют все точки, лежащие в данном круге. Таким образом, заданная фигура – это часть круга с центром в точке (2; –2) и радиусом
удовлетворяют все точки, лежащие в данном круге. Таким образом, заданная фигура – это часть круга с центром в точке (2; –2) и радиусом 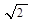 , лежащая правее прямой
, лежащая правее прямой  (рис. 4). Ответ:
(рис. 4). Ответ: 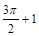 .
.
3.  Сколько целочисленных решений имеет неравенство
Сколько целочисленных решений имеет неравенство  ? Решение. Преобразуем левую часть следующим образом:
? Решение. Преобразуем левую часть следующим образом:  . Точки, удовлетворяющие данному неравенству, — это точки круга с центром в точке (–3; 2) и радиусом 2. Осталось только посчитать, сколько в этом круге точек с целыми координатами (рис. 5). Ответ: 13.
. Точки, удовлетворяющие данному неравенству, — это точки круга с центром в точке (–3; 2) и радиусом 2. Осталось только посчитать, сколько в этом круге точек с целыми координатами (рис. 5). Ответ: 13.
4.  Решить систему неравенств
Решить систему неравенств 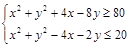 . Решение. Преобразуем систему к виду
. Решение. Преобразуем систему к виду 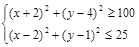 . Первое неравенство описывает внешность круга (включая границу) с центром в точке
. Первое неравенство описывает внешность круга (включая границу) с центром в точке  и радиусом 10. Второе — внутренность (включая границу) круга с центром в точке (2; 1) и радиусом 5 (рис. 6). Заметим, что расстояние между центрами этих окружностей равно
и радиусом 10. Второе — внутренность (включая границу) круга с центром в точке (2; 1) и радиусом 5 (рис. 6). Заметим, что расстояние между центрами этих окружностей равно 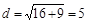 , т. е. равно разности радиусов большей окружности и меньшей окружности. Отсюда следует, что окружности касаются внутренним образом, и единственная точка, удовлетворяющая этим неравенствам, — это точка касания, симметричная точке (–2; 4) относительно точки
, т. е. равно разности радиусов большей окружности и меньшей окружности. Отсюда следует, что окружности касаются внутренним образом, и единственная точка, удовлетворяющая этим неравенствам, — это точка касания, симметричная точке (–2; 4) относительно точки  , т. е. точка (6; –2) (симметричность следует из того, что точка
, т. е. точка (6; –2) (симметричность следует из того, что точка  , лежит на середине отрезке между центром большей окружности (–2; 4) и точкой касания). Ответ: (6; –2).
, лежит на середине отрезке между центром большей окружности (–2; 4) и точкой касания). Ответ: (6; –2).
5. При каких значениях параметра 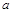 неравенство
неравенство 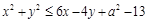 имеет не менее пяти целочисленных решений? Решение. Преобразовав данное неравенство, получим неравенство
имеет не менее пяти целочисленных решений? Решение. Преобразовав данное неравенство, получим неравенство  . Это неравенство задает круг с центром в точке (3; –2) и радиусом
. Это неравенство задает круг с центром в точке (3; –2) и радиусом 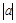 . Чтобы в этот круг вошло не меньше пяти целочисленных точек, нужно, чтобы его радиус был не меньше 1 (рис. 7). Ответ:
. Чтобы в этот круг вошло не меньше пяти целочисленных точек, нужно, чтобы его радиус был не меньше 1 (рис. 7). Ответ: 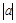
 .
.
6. 
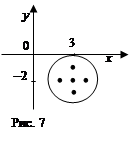 При каких значениях параметра система
При каких значениях параметра система 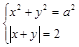 имеет ровно два решения? Решение. Как и множество других задач такого типа, эта задача гораздо проще решается графически. Уравнения этой системы задают две линии. Одну из них, не зависящую от параметра, мы будем называть «неподвижной», а ту, которая зависит от параметра, «движущейся». По сути дела, «движущаяся» линия — это семейство линий, но при решении удобнее представлять ее именно как линию, движущуюся по плоскости. Решение обычно состоит в том, что мы изображаем «неподвижную» линию, а затем мысленно двигаем по плоскости «движущуюся» линию, пытаясь найти такое ее положение, при котором выполняются условия задачи. Итак, изображаем «неподвижную» линию
имеет ровно два решения? Решение. Как и множество других задач такого типа, эта задача гораздо проще решается графически. Уравнения этой системы задают две линии. Одну из них, не зависящую от параметра, мы будем называть «неподвижной», а ту, которая зависит от параметра, «движущейся». По сути дела, «движущаяся» линия — это семейство линий, но при решении удобнее представлять ее именно как линию, движущуюся по плоскости. Решение обычно состоит в том, что мы изображаем «неподвижную» линию, а затем мысленно двигаем по плоскости «движущуюся» линию, пытаясь найти такое ее положение, при котором выполняются условия задачи. Итак, изображаем «неподвижную» линию 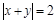 . Это две прямые
. Это две прямые 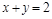 и
и 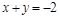 . Наша «движущаяся» линия — это окружность с центром в точке
. Наша «движущаяся» линия — это окружность с центром в точке  и переменным радиусом
и переменным радиусом 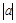 . Ее «движение» — это сжатие или растяжение в зависимости от изменения радиуса. Мы должны найти такое значение радиуса, при котором окружность имеет с прямыми ровно две общие точки. Мы видим, что есть только одно такое положение окружности, оно соответствует значению радиуса
. Ее «движение» — это сжатие или растяжение в зависимости от изменения радиуса. Мы должны найти такое значение радиуса, при котором окружность имеет с прямыми ровно две общие точки. Мы видим, что есть только одно такое положение окружности, оно соответствует значению радиуса 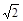 (рис.
(рис.  8). Ответ:
8). Ответ: 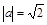 .
.
7. При каких значениях а система  равносильна системе
равносильна системе  ? Решение. Вспомним, что две системы называются равносильными, если они имеют одно и то же множество решений (или обе не имеют решения). Сразу можно отметить, что при
? Решение. Вспомним, что две системы называются равносильными, если они имеют одно и то же множество решений (или обе не имеют решения). Сразу можно отметить, что при 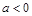 обе системы не имеют решения, значит, отрицательные значения параметра нужно включить в ответ. При
обе системы не имеют решения, значит, отрицательные значения параметра нужно включить в ответ. При 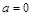 и та, и другая система имеет единственное решение (0; 0), следовательно, равносильность тоже выполняется. При положительных значениях
и та, и другая система имеет единственное решение (0; 0), следовательно, равносильность тоже выполняется. При положительных значениях 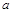 получаем в первой системе окружность радиуса
получаем в первой системе окружность радиуса 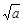 и прямую
и прямую  (рис. 10), а во второй системе ту же окружность и бесконечное множество прямых
(рис. 10), а во второй системе ту же окружность и бесконечное множество прямых 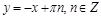 (см. рис. 9). Мы видим, что множества решений будут совпадать, если окружность не будет пересекать прямые
(см. рис. 9). Мы видим, что множества решений будут совпадать, если окружность не будет пересекать прямые  . Это будет в том случае, если радиус окружности меньше, чем
. Это будет в том случае, если радиус окружности меньше, чем  . Ответ:
. Ответ:  .
.
8.
При каких значениях параметра система
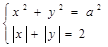
имеет ровно четыре решения?
Решение. Изображаем «неподвижную» линию, раскрывая знаки модуля отдельно в каждой четверти. Затем «сжимаем» и «растягиваем» окружность с центром в начале координат в поисках такого положения, чтобы она имела ровно четыре общие точки с «неподвижной» линией. Мы видим, что таких положений два (рис. 11). Одно соответствует значению радиуса 2, а второе —
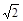
. Ответ:

.
9.
При каких значениях параметра система
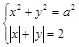
имеет ровно восемь решений?
Решение. Графическое исследование, проведенное в предыдущей задаче, показывает, что восемь точек пересечения будет, когда радиус находится в промежутке
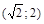
. Ответ:
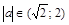
.
10. При каких значениях параметра 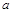 из неравенства
из неравенства 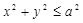 следует неравенство
следует неравенство 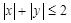 ? Решение. Вспомним, что означают слова «из неравенства (1) следует неравенство (2)». Они означают, что любая точка
? Решение. Вспомним, что означают слова «из неравенства (1) следует неравенство (2)». Они означают, что любая точка 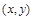 , удовлетворяющая неравенству (1), удовлетворяет также неравенству (2). Т. е. множество решений неравенства (1) содержится во множестве решений неравенства (2). Поскольку множество решений неравенства (1)
, удовлетворяющая неравенству (1), удовлетворяет также неравенству (2). Т. е. множество решений неравенства (1) содержится во множестве решений неравенства (2). Поскольку множество решений неравенства (1) 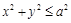 — это круг радиуса
— это круг радиуса 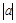 , а множество решений неравенства (2)
, а множество решений неравенства (2) 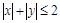 — это квадрат (рис. 11), то нужное расположение будет в том случае, когда радиус круга
— это квадрат (рис. 11), то нужное расположение будет в том случае, когда радиус круга 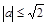 . Ответ:
. Ответ: 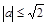 .
.
Рассмотрим небольшое усложнение этой задачи.
11. При каких значениях параметра 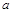 из неравенства
из неравенства  следует неравенство
следует неравенство 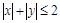 ? Решение. Понятно, что при
? Решение. Понятно, что при 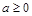 все предыдущие рассуждения пригодны, и при
все предыдущие рассуждения пригодны, и при 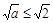 условие задачи выполнено. Что делать, когда
условие задачи выполнено. Что делать, когда 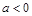 ? В этом случае неравенство (1) не имеет решений. Запомните, что изнеравенства, не имеющего решений, следует любое неравенство. (То же верно и для уравнений, систем уравнений или неравенств). Т. е. в этом случае условие задачи также выполнено. Ответ:
? В этом случае неравенство (1) не имеет решений. Запомните, что изнеравенства, не имеющего решений, следует любое неравенство. (То же верно и для уравнений, систем уравнений или неравенств). Т. е. в этом случае условие задачи также выполнено. Ответ:  .
.
12.  При каких значениях параметра
При каких значениях параметра 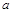 неравенство
неравенство 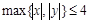 является следствием неравенства
является следствием неравенства 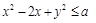 ? Решение. Неравенство (1)
? Решение. Неравенство (1) 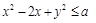
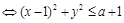 задает на плоскости круг с центром в точке (1; 0) радиуса
задает на плоскости круг с центром в точке (1; 0) радиуса 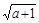 (при
(при 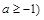 . Неравенство (2)
. Неравенство (2) 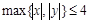 задает квадрат (рис. 12) с вершинами в точках
задает квадрат (рис. 12) с вершинами в точках 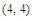 ,
, 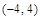 ,
, 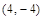 , (–4; –4).
, (–4; –4).  Чтобы круг с центром в точке (1; 0) полностью лежал в квадрате, нужно, чтобы его радиус был не больше 3. Т. е. должно выполняться неравенство
Чтобы круг с центром в точке (1; 0) полностью лежал в квадрате, нужно, чтобы его радиус был не больше 3. Т. е. должно выполняться неравенство 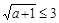
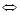
 . При
. При  неравенство (1) не имеет решений, следовательно, условие задачи также выполняется. Ответ:
неравенство (1) не имеет решений, следовательно, условие задачи также выполняется. Ответ: 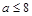 .
.
13. При каких значениях параметра система 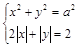 имеет ровно четыре решения? Решение. «Неподвижная» линия в данном случае ромб, и это усложняет задачу. Мы должны внимательно проделать мысленное «растяжение» окружности и проследить за количеством точек пересечения. Мы видим, что такое положение имеется, во-первых, в момент касания окружности и ромба (рис. 13), во-вторых, когда вершины ромба, лежащие на оси Оx, уже находятся внутри окружности, а вершины ромба на оси Оy еще вне окружности (рис. 15). Радиус окружности, вписанной в данный ромб, вычисляется как высота прямоугольного треугольника с катетами 1 и 2, опущенная на гипотенузу:
имеет ровно четыре решения? Решение. «Неподвижная» линия в данном случае ромб, и это усложняет задачу. Мы должны внимательно проделать мысленное «растяжение» окружности и проследить за количеством точек пересечения. Мы видим, что такое положение имеется, во-первых, в момент касания окружности и ромба (рис. 13), во-вторых, когда вершины ромба, лежащие на оси Оx, уже находятся внутри окружности, а вершины ромба на оси Оy еще вне окружности (рис. 15). Радиус окружности, вписанной в данный ромб, вычисляется как высота прямоугольного треугольника с катетами 1 и 2, опущенная на гипотенузу:
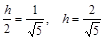 . Ответ:
. Ответ: 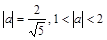 .
.
14.
При каких значениях параметра система
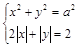
имеет ровно шесть решений?
Решение. Единственное подходящее расположение окружности показано на рис. 14. Ответ:

.
15.
При каких значениях параметра система
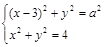
имеет единственное решение?
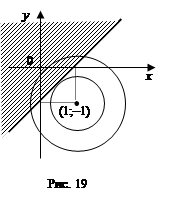
Решение. «Растягивая» окружность с центром в точке (3; 0), мы найдем два положения, в которых точка пересечения единственная (рис. 18). Они соответствуют значениям радиуса 1 и 5. Ответ:
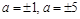
.
16. 
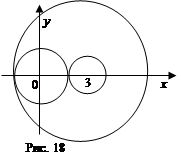 При каких значениях
При каких значениях 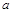 найдутся
найдутся  удовлетворяющие уравнению
удовлетворяющие уравнению  Решение. Данное уравнение равносильно системе
Решение. Данное уравнение равносильно системе 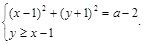 Изобразим окружность с центром в точке (1; –1) (ее радиус
Изобразим окружность с центром в точке (1; –1) (ее радиус  зависит от параметра), и область, лежащую выше прямой
зависит от параметра), и область, лежащую выше прямой 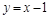 (рис. 19). Решение будет существовать, если радиус не меньше значения, соответствующего касанию:
(рис. 19). Решение будет существовать, если радиус не меньше значения, соответствующего касанию: 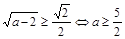 . Ответ:
. Ответ: 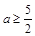 .
.
17.  При каких значениях параметра система
При каких значениях параметра система 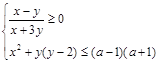 имеет хотя бы одно решение? Решение. Преобразуем второе неравенство к виду
имеет хотя бы одно решение? Решение. Преобразуем второе неравенство к виду  и увидим, что оно задает круг с центром в точке (0; 1) радиуса
и увидим, что оно задает круг с центром в точке (0; 1) радиуса 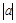 . Чтобы изобразить множество, задаваемое первым неравенством, нарисуем сначала прямые
. Чтобы изобразить множество, задаваемое первым неравенством, нарисуем сначала прямые  ,
, 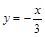 , причем вторую пунктиром, поскольку она не войдет во множество (рис. 20). Между этими прямыми выражения
, причем вторую пунктиром, поскольку она не войдет во множество (рис. 20). Между этими прямыми выражения  сохраняют знак, и несложно определить, какой именно. Неравенству
сохраняют знак, и несложно определить, какой именно. Неравенству 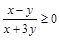 будет удовлетворять точки заштрихованной области (рис. 19). Мы видим, что решения системы будут тогда, когда радиус окружности не меньше, чем у окружности, касающейся прямой
будет удовлетворять точки заштрихованной области (рис. 19). Мы видим, что решения системы будут тогда, когда радиус окружности не меньше, чем у окружности, касающейся прямой  , т. е.
, т. е. 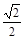 . Ответ:
. Ответ: 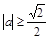 .
.
Рассмотрим теперь другой вид движения окружности: сдвиг.
18. При каких значениях параметра система  имеет единственное решение? Решение. В данном случае «неподвижная» линия — окружность с центром в начале координат и радиусом 2, а «движущаяся» линия — тоже окружность радиуса 2, но центр ее — точка
имеет единственное решение? Решение. В данном случае «неподвижная» линия — окружность с центром в начале координат и радиусом 2, а «движущаяся» линия — тоже окружность радиуса 2, но центр ее — точка 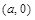 , зависящая от параметра, т. е. перемещающаяся по оси Оx. «Двигая» эту окружность, найдем два положения, в которых будет единственная точка пересечения (рис. 21). Ответ:
, зависящая от параметра, т. е. перемещающаяся по оси Оx. «Двигая» эту окружность, найдем два положения, в которых будет единственная точка пересечения (рис. 21). Ответ: 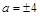 .
.
Аналогичным способом решаются задачи, в которых «неподвижной» линией является окружность, а «двигаются» линии другого вида.
19. При каких значениях параметра система 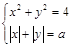 имеет ровно восемь решений? Решение. В данном случае «неподвижна» окружность с центром в начале координат и радиусом 2. «Движущаяся» линия — это квадрат с вершинами в точках
имеет ровно восемь решений? Решение. В данном случае «неподвижна» окружность с центром в начале координат и радиусом 2. «Движущаяся» линия — это квадрат с вершинами в точках 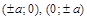 (при
(при 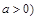 . Квадрат «растягивается» или «сжимается» в зависимости от изменения параметра. Используя рис. 11, несложно понять, при каких значениях параметра линии будут пересекаться в восьми точках. Ответ:
. Квадрат «растягивается» или «сжимается» в зависимости от изменения параметра. Используя рис. 11, несложно понять, при каких значениях параметра линии будут пересекаться в восьми точках. Ответ:  .
.
20. При каких значениях параметра 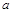 система
система  имеет хотя бы одно решение? Решение. Введем новые переменные
имеет хотя бы одно решение? Решение. Введем новые переменные 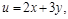
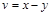 . Выразим из этих уравнений
. Выразим из этих уравнений 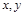 через новые переменные:
через новые переменные: 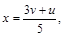
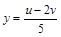 . Подставив эти выражения в первое уравнение, получим уравнение окружности:
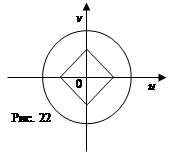
. Подставив эти выражения в первое уравнение, получим уравнение окружности: 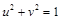 . Итак, в новых переменных получилась простая система
. Итак, в новых переменных получилась простая система  (рис. 22). «Растягивающийся» квадрат должен пересекаться с окружностью, отсюда
(рис. 22). «Растягивающийся» квадрат должен пересекаться с окружностью, отсюда 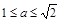 . Ответ:
. Ответ: 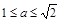 .
.
 Решим для сравнения внешне похожую задачу, которая тем не менее решается не графическим способом.
Решим для сравнения внешне похожую задачу, которая тем не менее решается не графическим способом.
21. При каких 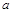 система
система  имеет не более двух решений? Решение. Введем новые переменные
имеет не более двух решений? Решение. Введем новые переменные 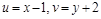 . Выразим из этих уравнений
. Выразим из этих уравнений 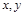 через новые переменные
через новые переменные 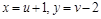 , и, подставив эти выражения в первое уравнение, получим систему
, и, подставив эти выражения в первое уравнение, получим систему 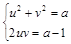 . Трудность в том, что второе уравнение задает гиперболу, а искать «касательное положение» окружности и гиперболы не очень просто. Проще заняться решением этой системы и в процессе решения разобраться, когда сколько решений. Предположим сначала
. Трудность в том, что второе уравнение задает гиперболу, а искать «касательное положение» окружности и гиперболы не очень просто. Проще заняться решением этой системы и в процессе решения разобраться, когда сколько решений. Предположим сначала 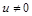 , выразим из второго уравнения
, выразим из второго уравнения  и подставим в первое:
и подставим в первое:  , или
, или  . Решаем биквадратное уравнение:
. Решаем биквадратное уравнение: 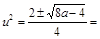
 . Отсюда видно, что при
. Отсюда видно, что при  решений нет. Если
решений нет. Если 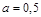 , то получаем два решения
, то получаем два решения 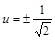 (и соответствующие значения
(и соответствующие значения  ). Если
). Если 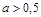 , то два решения получатся, если
, то два решения получатся, если 
 . Нужно вернуться к случаю, когда
. Нужно вернуться к случаю, когда 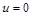 , значит,
, значит,  . Но система
. Но система 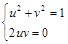 имеет четыре решения
имеет четыре решения  . Окончательный вывод: не более двух решений при
. Окончательный вывод: не более двух решений при  . Ответ:
. Ответ:  .
.
22. 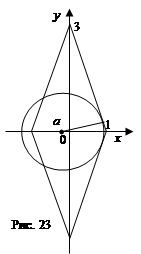 При каких значениях
При каких значениях 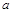 существует значение
существует значение  такое, что система
такое, что система  имеет ровно три решения? Решение. «Неподвижная» линия — ромб с вершинами
имеет ровно три решения? Решение. «Неподвижная» линия — ромб с вершинами 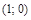 , (–1; 0),
, (–1; 0),  , (0; –3). «Движущаяся» линия — окружность с переменным центром и переменным радиусом. Наличие двух параметров, конечно, очень усложняет задачу. Мы должна сначала зафиксировать центр окружности в некоторой точке
, (0; –3). «Движущаяся» линия — окружность с переменным центром и переменным радиусом. Наличие двух параметров, конечно, очень усложняет задачу. Мы должна сначала зафиксировать центр окружности в некоторой точке 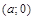 , а затем мысленно менять радиус, выясняя, можно ли при данном центре получить три точки пересечения. Заметим, что среди этих трех точек обязательно должна быть вершина ромба, лежащая на оси Ox. Поэтому можно рассматривать только окружности, проходящие через эти вершины, и выяснять, при каком расположении центра будут три точки пересечения. Рассмотрим сначала окружности, проходящие через точку (–1; 0). Мы видим (рис. 23), что три точки пересечения будут до тех пор, пока окружность не коснется противоположной стороны ромба. Вычислим положение центра в этот момент. Нужно потребовать, чтобы расстояние от точки
, а затем мысленно менять радиус, выясняя, можно ли при данном центре получить три точки пересечения. Заметим, что среди этих трех точек обязательно должна быть вершина ромба, лежащая на оси Ox. Поэтому можно рассматривать только окружности, проходящие через эти вершины, и выяснять, при каком расположении центра будут три точки пересечения. Рассмотрим сначала окружности, проходящие через точку (–1; 0). Мы видим (рис. 23), что три точки пересечения будут до тех пор, пока окружность не коснется противоположной стороны ромба. Вычислим положение центра в этот момент. Нужно потребовать, чтобы расстояние от точки 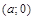 до прямой
до прямой  равнялось ее расстоянию до точки (–1; 0). Составим это уравнение:
равнялось ее расстоянию до точки (–1; 0). Составим это уравнение: 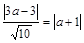 . Учитывая, что
. Учитывая, что 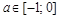 , получаем
, получаем  . Мы нашли положение центра в момент касания, а условию задачи удовлетворяют значения
. Мы нашли положение центра в момент касания, а условию задачи удовлетворяют значения 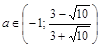 . Еще одно подходящее положение возникнет в тот момент, когда окружность пройдет через три вершины
. Еще одно подходящее положение возникнет в тот момент, когда окружность пройдет через три вершины  (0; 3),(0; –3). Подставив эти точки в уравнение окружности
(0; 3),(0; –3). Подставив эти точки в уравнение окружности 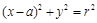 , получим
, получим  . Для окружностей, проходящих через точку (1; 0), получим симметричные значения. Ответ:
. Для окружностей, проходящих через точку (1; 0), получим симметричные значения. Ответ: 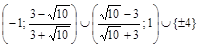 .
.
23. 
Найти значение
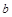
такое, что наименьшее положительное значение
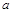
, при котором система
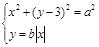
имеет решение, равно 2.
Решение. Линия
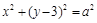
является окружностью с центром в точке (0; 3) радиуса
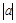
, линия
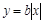
— «уголок» с вершиной в начале координат,
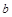
— угловой коэффициент правого луча (рис. 24). Очевидно, наименьшее значение радиуса, при котором линии пересекаются — это такой радиус, при котором окружность касается сторон «уголка». По условию это радиус, равный 2. Обозначим через
А центр окружности, через
В точку касания (рис. 24). Тогда
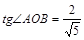
, а угловой коэффициент прямой
ОВ равен
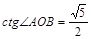
. Ответ:
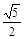
.
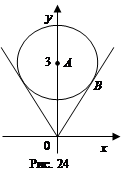
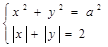 имеет ровно четыре решения? Решение. Изображаем «неподвижную» линию, раскрывая знаки модуля отдельно в каждой четверти. Затем «сжимаем» и «растягиваем» окружность с центром в начале координат в поисках такого положения, чтобы она имела ровно четыре общие точки с «неподвижной» линией. Мы видим, что таких положений два (рис. 11). Одно соответствует значению радиуса 2, а второе —
имеет ровно четыре решения? Решение. Изображаем «неподвижную» линию, раскрывая знаки модуля отдельно в каждой четверти. Затем «сжимаем» и «растягиваем» окружность с центром в начале координат в поисках такого положения, чтобы она имела ровно четыре общие точки с «неподвижной» линией. Мы видим, что таких положений два (рис. 11). Одно соответствует значению радиуса 2, а второе — 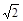 . Ответ:
. Ответ:  .
.
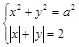 имеет ровно восемь решений? Решение. Графическое исследование, проведенное в предыдущей задаче, показывает, что восемь точек пересечения будет, когда радиус находится в промежутке
имеет ровно восемь решений? Решение. Графическое исследование, проведенное в предыдущей задаче, показывает, что восемь точек пересечения будет, когда радиус находится в промежутке 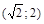 . Ответ:
. Ответ: 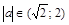 .
.
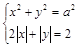 имеет ровно шесть решений? Решение. Единственное подходящее расположение окружности показано на рис. 14. Ответ:
имеет ровно шесть решений? Решение. Единственное подходящее расположение окружности показано на рис. 14. Ответ:  .
.
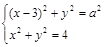 имеет единственное решение? Решение. «Растягивая» окружность с центром в точке (3; 0), мы найдем два положения, в которых точка пересечения единственная (рис. 18). Они соответствуют значениям радиуса 1 и 5. Ответ:
имеет единственное решение? Решение. «Растягивая» окружность с центром в точке (3; 0), мы найдем два положения, в которых точка пересечения единственная (рис. 18). Они соответствуют значениям радиуса 1 и 5. Ответ: 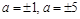 .
.
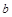 такое, что наименьшее положительное значение
такое, что наименьшее положительное значение 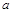 , при котором система
, при котором система 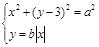 имеет решение, равно 2. Решение. Линия
имеет решение, равно 2. Решение. Линия 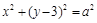 является окружностью с центром в точке (0; 3) радиуса
является окружностью с центром в точке (0; 3) радиуса 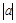 , линия
, линия 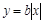 — «уголок» с вершиной в начале координат,
— «уголок» с вершиной в начале координат, 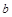 — угловой коэффициент правого луча (рис. 24). Очевидно, наименьшее значение радиуса, при котором линии пересекаются — это такой радиус, при котором окружность касается сторон «уголка». По условию это радиус, равный 2. Обозначим через А центр окружности, через В точку касания (рис. 24). Тогда
— угловой коэффициент правого луча (рис. 24). Очевидно, наименьшее значение радиуса, при котором линии пересекаются — это такой радиус, при котором окружность касается сторон «уголка». По условию это радиус, равный 2. Обозначим через А центр окружности, через В точку касания (рис. 24). Тогда 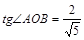 , а угловой коэффициент прямой ОВ равен
, а угловой коэффициент прямой ОВ равен 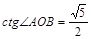 . Ответ:
. Ответ: 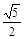 .
.

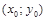 и радиусом
и радиусом  :
: 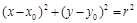 . Понятно ли, почему оно именно такое? Слева записан квадрат расстояния от точки
. Понятно ли, почему оно именно такое? Слева записан квадрат расстояния от точки 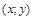 до точки
до точки 
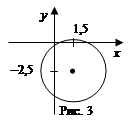 Изобразить на плоскости следующие окружности: а)
Изобразить на плоскости следующие окружности: а) 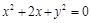 ; б)
; б)  ; в)
; в) 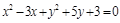 . Решение. а) Нужно сформировать в левой части полные квадраты:
. Решение. а) Нужно сформировать в левой части полные квадраты: 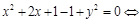
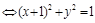 . Итак, мы получили окружность с центром в точке (–1; 0) радиуса 1 (рис. 1). б) Сформировав полные квадраты, получим уравнение
. Итак, мы получили окружность с центром в точке (–1; 0) радиуса 1 (рис. 1). б) Сформировав полные квадраты, получим уравнение 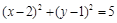 . Это окружность с центром в точке (2; 1) и радиусом
. Это окружность с центром в точке (2; 1) и радиусом 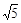 (рис. 2). Чтобы точнее изобразить эту окружность, заметим, что она проходит через начало координат: это видно из уравнения. в) Получим уравнение
(рис. 2). Чтобы точнее изобразить эту окружность, заметим, что она проходит через начало координат: это видно из уравнения. в) Получим уравнение  (рис. 3).
(рис. 3). Найти площадь фигуры, заданной неравенствами
Найти площадь фигуры, заданной неравенствами 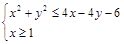 . Решение. Изобразим множество точек, удовлетворяющих первому неравенству. Для этого перепишем его в таком виде:
. Решение. Изобразим множество точек, удовлетворяющих первому неравенству. Для этого перепишем его в таком виде: 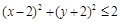 . Граница этого множества — окружность
. Граница этого множества — окружность 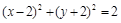 с центром в точке
с центром в точке  и радиусом
и радиусом 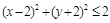 удовлетворяют все точки, лежащие в данном круге. Таким образом, заданная фигура – это часть круга с центром в точке (2; –2) и радиусом
удовлетворяют все точки, лежащие в данном круге. Таким образом, заданная фигура – это часть круга с центром в точке (2; –2) и радиусом 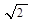 , лежащая правее прямой
, лежащая правее прямой  (рис. 4). Ответ:
(рис. 4). Ответ: 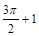 .
. Сколько целочисленных решений имеет неравенство
Сколько целочисленных решений имеет неравенство  ? Решение. Преобразуем левую часть следующим образом:
? Решение. Преобразуем левую часть следующим образом:  . Точки, удовлетворяющие данному неравенству, — это точки круга с центром в точке (–3; 2) и радиусом 2. Осталось только посчитать, сколько в этом круге точек с целыми координатами (рис. 5). Ответ: 13.
. Точки, удовлетворяющие данному неравенству, — это точки круга с центром в точке (–3; 2) и радиусом 2. Осталось только посчитать, сколько в этом круге точек с целыми координатами (рис. 5). Ответ: 13. Решить систему неравенств
Решить систему неравенств 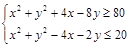 . Решение. Преобразуем систему к виду
. Решение. Преобразуем систему к виду 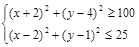 . Первое неравенство описывает внешность круга (включая границу) с центром в точке
. Первое неравенство описывает внешность круга (включая границу) с центром в точке  и радиусом 10. Второе — внутренность (включая границу) круга с центром в точке (2; 1) и радиусом 5 (рис. 6). Заметим, что расстояние между центрами этих окружностей равно
и радиусом 10. Второе — внутренность (включая границу) круга с центром в точке (2; 1) и радиусом 5 (рис. 6). Заметим, что расстояние между центрами этих окружностей равно 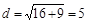 , т. е. равно разности радиусов большей окружности и меньшей окружности. Отсюда следует, что окружности касаются внутренним образом, и единственная точка, удовлетворяющая этим неравенствам, — это точка касания, симметричная точке (–2; 4) относительно точки
, т. е. равно разности радиусов большей окружности и меньшей окружности. Отсюда следует, что окружности касаются внутренним образом, и единственная точка, удовлетворяющая этим неравенствам, — это точка касания, симметричная точке (–2; 4) относительно точки  , т. е. точка (6; –2) (симметричность следует из того, что точка
, т. е. точка (6; –2) (симметричность следует из того, что точка 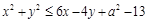 имеет не менее пяти целочисленных решений? Решение. Преобразовав данное неравенство, получим неравенство
имеет не менее пяти целочисленных решений? Решение. Преобразовав данное неравенство, получим неравенство  . Это неравенство задает круг с центром в точке (3; –2) и радиусом
. Это неравенство задает круг с центром в точке (3; –2) и радиусом  .
.
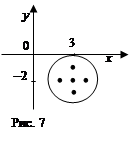 При каких значениях параметра система
При каких значениях параметра система 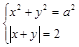 имеет ровно два решения? Решение. Как и множество других задач такого типа, эта задача гораздо проще решается графически. Уравнения этой системы задают две линии. Одну из них, не зависящую от параметра, мы будем называть «неподвижной», а ту, которая зависит от параметра, «движущейся». По сути дела, «движущаяся» линия — это семейство линий, но при решении удобнее представлять ее именно как линию, движущуюся по плоскости. Решение обычно состоит в том, что мы изображаем «неподвижную» линию, а затем мысленно двигаем по плоскости «движущуюся» линию, пытаясь найти такое ее положение, при котором выполняются условия задачи. Итак, изображаем «неподвижную» линию
имеет ровно два решения? Решение. Как и множество других задач такого типа, эта задача гораздо проще решается графически. Уравнения этой системы задают две линии. Одну из них, не зависящую от параметра, мы будем называть «неподвижной», а ту, которая зависит от параметра, «движущейся». По сути дела, «движущаяся» линия — это семейство линий, но при решении удобнее представлять ее именно как линию, движущуюся по плоскости. Решение обычно состоит в том, что мы изображаем «неподвижную» линию, а затем мысленно двигаем по плоскости «движущуюся» линию, пытаясь найти такое ее положение, при котором выполняются условия задачи. Итак, изображаем «неподвижную» линию 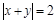 . Это две прямые
. Это две прямые 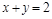 и
и 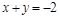 . Наша «движущаяся» линия — это окружность с центром в точке
. Наша «движущаяся» линия — это окружность с центром в точке  и переменным радиусом
и переменным радиусом  8). Ответ:
8). Ответ: 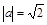 .
. равносильна системе
равносильна системе  ? Решение. Вспомним, что две системы называются равносильными, если они имеют одно и то же множество решений (или обе не имеют решения). Сразу можно отметить, что при
? Решение. Вспомним, что две системы называются равносильными, если они имеют одно и то же множество решений (или обе не имеют решения). Сразу можно отметить, что при 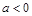 обе системы не имеют решения, значит, отрицательные значения параметра нужно включить в ответ. При
обе системы не имеют решения, значит, отрицательные значения параметра нужно включить в ответ. При 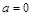 и та, и другая система имеет единственное решение (0; 0), следовательно, равносильность тоже выполняется. При положительных значениях
и та, и другая система имеет единственное решение (0; 0), следовательно, равносильность тоже выполняется. При положительных значениях 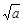 и прямую
и прямую  (рис. 10), а во второй системе ту же окружность и бесконечное множество прямых
(рис. 10), а во второй системе ту же окружность и бесконечное множество прямых 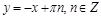 (см. рис. 9). Мы видим, что множества решений будут совпадать, если окружность не будет пересекать прямые
(см. рис. 9). Мы видим, что множества решений будут совпадать, если окружность не будет пересекать прямые  . Это будет в том случае, если радиус окружности меньше, чем
. Это будет в том случае, если радиус окружности меньше, чем  . Ответ:
. Ответ:  .
.

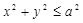 следует неравенство
следует неравенство 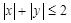 ? Решение. Вспомним, что означают слова «из неравенства (1) следует неравенство (2)». Они означают, что любая точка
? Решение. Вспомним, что означают слова «из неравенства (1) следует неравенство (2)». Они означают, что любая точка 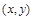 , удовлетворяющая неравенству (1), удовлетворяет также неравенству (2). Т. е. множество решений неравенства (1) содержится во множестве решений неравенства (2). Поскольку множество решений неравенства (1)
, удовлетворяющая неравенству (1), удовлетворяет также неравенству (2). Т. е. множество решений неравенства (1) содержится во множестве решений неравенства (2). Поскольку множество решений неравенства (1) 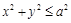 — это круг радиуса
— это круг радиуса 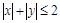 — это квадрат (рис. 11), то нужное расположение будет в том случае, когда радиус круга
— это квадрат (рис. 11), то нужное расположение будет в том случае, когда радиус круга 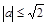 . Ответ:
. Ответ:  следует неравенство
следует неравенство 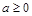 все предыдущие рассуждения пригодны, и при
все предыдущие рассуждения пригодны, и при 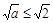 условие задачи выполнено. Что делать, когда
условие задачи выполнено. Что делать, когда  .
. При каких значениях параметра
При каких значениях параметра 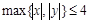 является следствием неравенства
является следствием неравенства 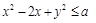 ? Решение. Неравенство (1)
? Решение. Неравенство (1) 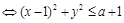 задает на плоскости круг с центром в точке (1; 0) радиуса
задает на плоскости круг с центром в точке (1; 0) радиуса 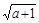 (при
(при 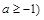 . Неравенство (2)
. Неравенство (2) 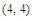 ,
, 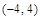 ,
, 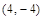 , (–4; –4).
, (–4; –4).  Чтобы круг с центром в точке (1; 0) полностью лежал в квадрате, нужно, чтобы его радиус был не больше 3. Т. е. должно выполняться неравенство
Чтобы круг с центром в точке (1; 0) полностью лежал в квадрате, нужно, чтобы его радиус был не больше 3. Т. е. должно выполняться неравенство 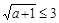
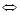
 . При
. При  неравенство (1) не имеет решений, следовательно, условие задачи также выполняется. Ответ:
неравенство (1) не имеет решений, следовательно, условие задачи также выполняется. Ответ: 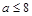 .
.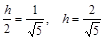 . Ответ:
. Ответ: 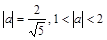 .
.

 При каких значениях
При каких значениях  удовлетворяющие уравнению
удовлетворяющие уравнению  Решение. Данное уравнение равносильно системе
Решение. Данное уравнение равносильно системе 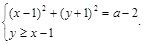 Изобразим окружность с центром в точке (1; –1) (ее радиус
Изобразим окружность с центром в точке (1; –1) (ее радиус  зависит от параметра), и область, лежащую выше прямой
зависит от параметра), и область, лежащую выше прямой 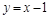 (рис. 19). Решение будет существовать, если радиус не меньше значения, соответствующего касанию:
(рис. 19). Решение будет существовать, если радиус не меньше значения, соответствующего касанию: 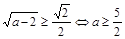 . Ответ:
. Ответ: 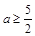 .
. При каких значениях параметра система
При каких значениях параметра система 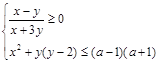 имеет хотя бы одно решение? Решение. Преобразуем второе неравенство к виду
имеет хотя бы одно решение? Решение. Преобразуем второе неравенство к виду  и увидим, что оно задает круг с центром в точке (0; 1) радиуса
и увидим, что оно задает круг с центром в точке (0; 1) радиуса  ,
, 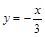 , причем вторую пунктиром, поскольку она не войдет во множество (рис. 20). Между этими прямыми выражения
, причем вторую пунктиром, поскольку она не войдет во множество (рис. 20). Между этими прямыми выражения  сохраняют знак, и несложно определить, какой именно. Неравенству
сохраняют знак, и несложно определить, какой именно. Неравенству 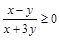 будет удовлетворять точки заштрихованной области (рис. 19). Мы видим, что решения системы будут тогда, когда радиус окружности не меньше, чем у окружности, касающейся прямой
будет удовлетворять точки заштрихованной области (рис. 19). Мы видим, что решения системы будут тогда, когда радиус окружности не меньше, чем у окружности, касающейся прямой 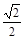 . Ответ:
. Ответ: 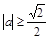 .
. имеет единственное решение? Решение. В данном случае «неподвижная» линия — окружность с центром в начале координат и радиусом 2, а «движущаяся» линия — тоже окружность радиуса 2, но центр ее — точка
имеет единственное решение? Решение. В данном случае «неподвижная» линия — окружность с центром в начале координат и радиусом 2, а «движущаяся» линия — тоже окружность радиуса 2, но центр ее — точка 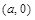 , зависящая от параметра, т. е. перемещающаяся по оси Оx. «Двигая» эту окружность, найдем два положения, в которых будет единственная точка пересечения (рис. 21). Ответ:
, зависящая от параметра, т. е. перемещающаяся по оси Оx. «Двигая» эту окружность, найдем два положения, в которых будет единственная точка пересечения (рис. 21). Ответ: 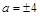 .
.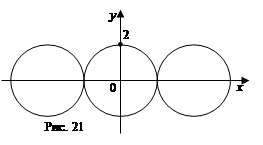
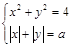 имеет ровно восемь решений? Решение. В данном случае «неподвижна» окружность с центром в начале координат и радиусом 2. «Движущаяся» линия — это квадрат с вершинами в точках
имеет ровно восемь решений? Решение. В данном случае «неподвижна» окружность с центром в начале координат и радиусом 2. «Движущаяся» линия — это квадрат с вершинами в точках 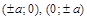 (при
(при 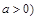 . Квадрат «растягивается» или «сжимается» в зависимости от изменения параметра. Используя рис. 11, несложно понять, при каких значениях параметра линии будут пересекаться в восьми точках. Ответ:
. Квадрат «растягивается» или «сжимается» в зависимости от изменения параметра. Используя рис. 11, несложно понять, при каких значениях параметра линии будут пересекаться в восьми точках. Ответ:  .
. имеет хотя бы одно решение? Решение. Введем новые переменные
имеет хотя бы одно решение? Решение. Введем новые переменные 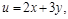
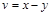 . Выразим из этих уравнений
. Выразим из этих уравнений 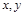 через новые переменные:
через новые переменные: 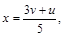
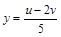 . Подставив эти выражения в первое уравнение, получим уравнение окружности:
. Подставив эти выражения в первое уравнение, получим уравнение окружности: 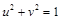 . Итак, в новых переменных получилась простая система
. Итак, в новых переменных получилась простая система  (рис. 22). «Растягивающийся» квадрат должен пересекаться с окружностью, отсюда
(рис. 22). «Растягивающийся» квадрат должен пересекаться с окружностью, отсюда 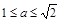 . Ответ:
. Ответ:  Решим для сравнения внешне похожую задачу, которая тем не менее решается не графическим способом.
Решим для сравнения внешне похожую задачу, которая тем не менее решается не графическим способом. имеет не более двух решений? Решение. Введем новые переменные
имеет не более двух решений? Решение. Введем новые переменные 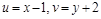 . Выразим из этих уравнений
. Выразим из этих уравнений 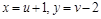 , и, подставив эти выражения в первое уравнение, получим систему
, и, подставив эти выражения в первое уравнение, получим систему 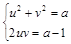 . Трудность в том, что второе уравнение задает гиперболу, а искать «касательное положение» окружности и гиперболы не очень просто. Проще заняться решением этой системы и в процессе решения разобраться, когда сколько решений. Предположим сначала
. Трудность в том, что второе уравнение задает гиперболу, а искать «касательное положение» окружности и гиперболы не очень просто. Проще заняться решением этой системы и в процессе решения разобраться, когда сколько решений. Предположим сначала 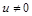 , выразим из второго уравнения
, выразим из второго уравнения  и подставим в первое:
и подставим в первое:  , или
, или  . Решаем биквадратное уравнение:
. Решаем биквадратное уравнение: 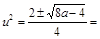
 . Отсюда видно, что при
. Отсюда видно, что при  решений нет. Если
решений нет. Если 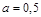 , то получаем два решения
, то получаем два решения 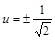 (и соответствующие значения
(и соответствующие значения  ). Если
). Если 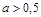 , то два решения получатся, если
, то два решения получатся, если 
 . Нужно вернуться к случаю, когда
. Нужно вернуться к случаю, когда 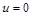 , значит,
, значит,  . Но система
. Но система 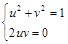 имеет четыре решения
имеет четыре решения  . Окончательный вывод: не более двух решений при
. Окончательный вывод: не более двух решений при  . Ответ:
. Ответ: 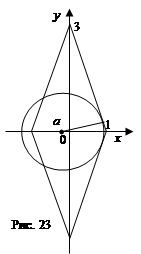 При каких значениях
При каких значениях  имеет ровно три решения? Решение. «Неподвижная» линия — ромб с вершинами
имеет ровно три решения? Решение. «Неподвижная» линия — ромб с вершинами 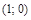 , (–1; 0),
, (–1; 0),  , (0; –3). «Движущаяся» линия — окружность с переменным центром и переменным радиусом. Наличие двух параметров, конечно, очень усложняет задачу. Мы должна сначала зафиксировать центр окружности в некоторой точке
, (0; –3). «Движущаяся» линия — окружность с переменным центром и переменным радиусом. Наличие двух параметров, конечно, очень усложняет задачу. Мы должна сначала зафиксировать центр окружности в некоторой точке 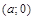 , а затем мысленно менять радиус, выясняя, можно ли при данном центре получить три точки пересечения. Заметим, что среди этих трех точек обязательно должна быть вершина ромба, лежащая на оси Ox. Поэтому можно рассматривать только окружности, проходящие через эти вершины, и выяснять, при каком расположении центра будут три точки пересечения. Рассмотрим сначала окружности, проходящие через точку (–1; 0). Мы видим (рис. 23), что три точки пересечения будут до тех пор, пока окружность не коснется противоположной стороны ромба. Вычислим положение центра в этот момент. Нужно потребовать, чтобы расстояние от точки
, а затем мысленно менять радиус, выясняя, можно ли при данном центре получить три точки пересечения. Заметим, что среди этих трех точек обязательно должна быть вершина ромба, лежащая на оси Ox. Поэтому можно рассматривать только окружности, проходящие через эти вершины, и выяснять, при каком расположении центра будут три точки пересечения. Рассмотрим сначала окружности, проходящие через точку (–1; 0). Мы видим (рис. 23), что три точки пересечения будут до тех пор, пока окружность не коснется противоположной стороны ромба. Вычислим положение центра в этот момент. Нужно потребовать, чтобы расстояние от точки  равнялось ее расстоянию до точки (–1; 0). Составим это уравнение:
равнялось ее расстоянию до точки (–1; 0). Составим это уравнение: 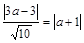 . Учитывая, что
. Учитывая, что 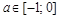 , получаем
, получаем  . Мы нашли положение центра в момент касания, а условию задачи удовлетворяют значения
. Мы нашли положение центра в момент касания, а условию задачи удовлетворяют значения 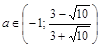 . Еще одно подходящее положение возникнет в тот момент, когда окружность пройдет через три вершины
. Еще одно подходящее положение возникнет в тот момент, когда окружность пройдет через три вершины  (0; 3),(0; –3). Подставив эти точки в уравнение окружности
(0; 3),(0; –3). Подставив эти точки в уравнение окружности 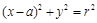 , получим
, получим  . Для окружностей, проходящих через точку (1; 0), получим симметричные значения. Ответ:
. Для окружностей, проходящих через точку (1; 0), получим симметричные значения. Ответ: 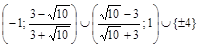 .
.




