Прямая в пространстве и различные способы ее задания.
24. При каких значениях параметра система 25. При каких значениях параметра система 26. При каких 27. При каких значениях параметра система 28. При каких значениях параметра системы 29. При каких значениях параметра неравенство 30. Найти все целочисленные решения системы 31. Найти все целочисленные решения системы 32. Определить число целочисленных решений системы 33. При каких значениях параметра система 34. При каких значениях параметра из неравенства 35. Найти значение Прямая в пространстве и различные способы ее задания.
Уравнение прямой, проходящей через заданную точку
и называется векторно-параметрическим уравнением прямой. Здесь
Если в уравнении (1) перейти к координатам векторов, то получаются параметрические уравнения прямой:
Если из уравнений (2) исключить параметр t, то получаются канонические уравнения прямой:
Уравнения прямой, проходящей через две точки М1(x1,y1,z1) и М2(x2,y2,z2) имеют вид:
Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей
Т.о., прямая определяется совместным заданием системы двух линейных уравнений:
---------------------------------------------------------------------------------------------------------------- Прямая в пространстве. Стр. 1. Они называются общими уравнениями прямой. В этом случае направляющий вектор прямой можно определить следующим образом:
Пусть заданы две прямые:
Пример 1. Составить уравнения прямой, проходящей через точку M 1(2;0;–3) параллельно: а) вектору Решение. а) Так как искомая прямая параллельна вектору
б) Так как искомая прямая параллельна прямой с направляющим вектором
в) Так как искомая прямая параллельна оси Ox, значит, она параллельна вектору
Случай, когда хотя бы в одном знаменателе канонических уравнений прямой получается ноль, не лишено смысла, но свидетельствует о том, что направляющий вектор прямой имеет одну или две нулевые координаты. В таких случаях лучше записывать параметрические уравнения прямой:
---------------------------------------------------------------------------------------------------------------- Прямая в пространстве. Стр. 2. Пример 2. Составить канонические уравнения прямой Решение. Для составления канонических уравнений прямой необходимо знать направляющий вектор
В качестве фиксированной точки можно выбрать любую точку прямой. Зададим одну из координат искомой точки произвольно. Пусть z=0. Тогда
Теперь составляем канонические уравнения прямой, зная ее направляющий вектор
|

 имеет ровно восемь решений? Ответ:
имеет ровно восемь решений? Ответ:  .
. имеет ровно три решения? Ответ:
имеет ровно три решения? Ответ:  .
.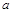 система
система  имеет ровно три решения? Ответ:
имеет ровно три решения? Ответ: 
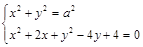 имеет а) решение; б) единственное решение? Ответ:
имеет а) решение; б) единственное решение? Ответ:  ; б)
; б) 
 .
. и
и  равносильны? Ответ:
равносильны? Ответ:  .
.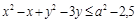 не имеет целочисленных решений? Ответ:
не имеет целочисленных решений? Ответ:  .
. . Ответ: (3; –4); (4; –5).
. Ответ: (3; –4); (4; –5). . Ответ: (–7; 7); (–6; 6).
. Ответ: (–7; 7); (–6; 6). . Ответ: 2.
. Ответ: 2. не имеет решений? Ответ:
не имеет решений? Ответ: 
 следует неравенство
следует неравенство 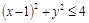 ? Ответ:
? Ответ:  .
.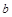 такое, что наименьшее положительное значение
такое, что наименьшее положительное значение 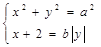 имеет решение, равно 1. Ответ:
имеет решение, равно 1. Ответ:  .
. параллельно вектору
параллельно вектору  имеет вид:
имеет вид: (1)
(1) – радиус-вектор произвольной точки М(x,y,z) прямой;
– радиус-вектор произвольной точки М(x,y,z) прямой;  – радиус-вектор фиксированной точки
– радиус-вектор фиксированной точки  называется направляющим вектором прямой, а его координаты
называется направляющим вектором прямой, а его координаты  – направляющими коэффициентами прямой.
– направляющими коэффициентами прямой.
 (2)
(2) (3)
(3) (4)
(4)
 (5)
(5) .
. и
и  . Тогда условие параллельности прямых записывается в виде:
. Тогда условие параллельности прямых записывается в виде:  , условие перпендикулярности – в виде:
, условие перпендикулярности – в виде:  , а угол
, а угол  между ними вычисляется по формуле
между ними вычисляется по формуле .
. ; б) прямой
; б) прямой  ; в) оси Ox.
; в) оси Ox. 
 , то этот вектор параллелен искомой прямой, значит, его можно принять за направляющий вектор искомой прямой. Тогда канонические уравнения искомой прямой имеют вид:
, то этот вектор параллелен искомой прямой, значит, его можно принять за направляющий вектор искомой прямой. Тогда канонические уравнения искомой прямой имеют вид: .
. , т.е.
, т.е.  и канонические уравнения искомой прямой имеют вид:
и канонические уравнения искомой прямой имеют вид: .
.

 ,
,  , то
, то
 .
.



