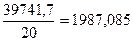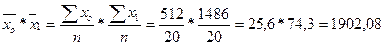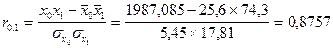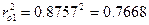Первенство России. Велоспорт-шоссе
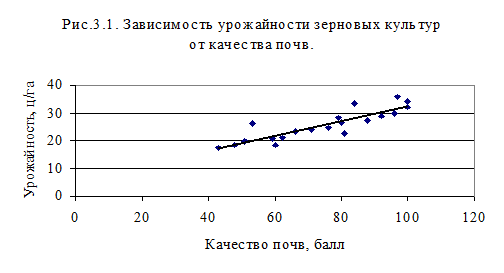
Условие. В табл. 3.15 представлены данные выборочного наблюдения о качестве почв и урожайности зерновых культур. Требуется решить уравнение и определить показатели тесноты связи урожайности с качеством почв. Решение. 1.Построим график, чтобы установить форму связи между признаками (рис.3.1). Для этого на корреляционное поле нанесем фактические значения зависимой переменной (х0 - урожайность, ц с 1 га) при соответствующих
значениях независимой переменной (х1 - качество почв).
Расположение точек на корреляционном поле позволяет сделать вывод о том, что связь между переменными близка к линейной. Запишем уравнение связи урожайности с качеством почв: х0=а0+а1х1, где а0 и а1 - неизвестные параметры уравнения. 2.Составим систему нормальных уравнений, необходимых для определения неизвестных параметров а0 и а1:
3. Рассчитаем величины 4. Из таблицы 3.15 подставим в систему нормальных уравнений соответствующие конкретные величины: 512,0 = 20 а0 + 1486 а1 39741,7 = 1486 а0 + 116752 а1 5. Решим систему уравнений и определим неизвестные параметры а0 и а1, для чего: а) разделим оба уравнения на коэффициенты при а0 (первое уравнение - на 20, второе - на 1486): 25,600 = а0 + 74,300 а1 26,744 = а0 + 78,568 а1 б) вычтем из второго уравнения первое: 1,144 = 4,268 а 1 в) определим параметр а 1: а 1 = 1,144: 4,268 = 0,268 г) подставим в одно из уравнений значение параметра а 1 и исчислим параметр а 0: а 0 = 25,600 - 74,300 х 0,265 = 5,688 Таблица -3.15. Данные для определения показателей корреляционной связи
6. Подставим найденные значения параметров а 0 и а 1 в уравнение связи:
7. Для расчета показателей тесноты связи определим величины: -среднее квадратическое отклонение по урожайности:
-среднее квадратическое отклонение по качеству почв:
- среднее произведение зависимой и независимой переменной:
-произведение средних величин зависимой и независимой переменной
8.Рассчитаем коэффициент корреляции по формуле:
9. Рассчитаем коэффициент детерминации
10. Сделаем вывод. Судя по уравнению регрессии Коэффициент корреляции 0,8757 показывает, что связь между изучаемыми признаками тесная. Коэффициент детерминации 0,7668 показывает, что 76,68% вариации урожайности объясняется вариацией плодородия почв.
Первенство России. Велоспорт-шоссе
|

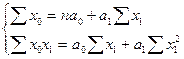
 которые нужны для решения системы нормальных уравнений и определения показателей тесноты связи (табл.5.1).
которые нужны для решения системы нормальных уравнений и определения показателей тесноты связи (табл.5.1).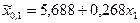
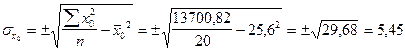
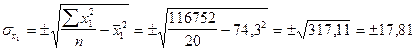
 =
=