Зміст лекції. Сила Ампера. Сила Лоренца. Рух заряджених частинок в електричному та магнітному полях. Взаємодія двох провідників.
Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила d F, с которой магнитное поле действует на элемент dl проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной d l проводника на магнитную индукцию В:
Направление вектора d F может быть найдено, по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера вычисляется по формуле dF = IB dl sin α где α - угол между векторами d l и В.
Ток I 1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B 1 задается правилом правого винта, его модуль по формуле равен
Направление силы d F 1, с которой поле B 1 действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, с учетом того, что угол α между элементами тока I 2 и вектором B 1прямой, равен dF 1= I 2 B 1 dl, или, подставляя значение для B 1, получим
Рассуждая аналогично, можно показать, что сила d F 2, с которой магнитное поле тока I 2 действует на элемент dl первого проводника с током I 1, направлена в противоположную сторону и по модулю равна
Сравнение этих выражений показывает, что dF 1= dF 2, т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая єтой же формулой. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля. Если два параллельных проводника с током находятся в вакууме (μ =1), то сила взаимодействия на единицу длины проводника, равна
Для нахождения числового значения μо воспользуемся определением ампера, согласно которому при I 1= I 2=1 A и R =1 м μo=4л.10-7 H/A2 = 4π.10-7 Гн/м, где генри (Гн) - единица индуктивности. Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера запишется в виде dF=IBdl, откуда Единица магнитной индукции - тесла (Тл): 1 Тл - магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А: 1Тл=1Н/(А.м). Так как μo = 4.l0-7 H / A 2, а в случае вакуума (μ=1), согласно, В= μо H, то для данного случая H = B /μo. Единица напряженности магнитного поля - ампер на метр (А/м): 1 А/м - напряженность такого поля, магнитная индукция которого в вакууме равна 4π.10-7 Тл. Действие магнитного поля на движущийся заряд. Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой F = Q [ vB ], где В - индукция магнитного поля, в котором заряд движется.
Отметим еще раз, что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды. Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано для определения вектора магнитной индукции В. Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется. Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил -силы, действующей со стороны электрического поля, и силы Лоренца: F = Q E + Q [ vB ]. Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля. Движение заряженных частиц в магнитном поле. Выражение для силы Лоренца позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных нолях. Будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и В равен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F = Q [ vB ] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться но окружности, радиус r которой определяется из условия QvB = mv 2/ r, откуда
Подставив сюда выражение, получим т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду(Q / m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)). На этом основано действие циклических ускорителей заряженных частиц. Если скорость v заряженной частицы направлена под углом a к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1)равномерного прямолинейного движения вдоль поля со скоростью 2) равномерного движения со скоростью h =2p mv cos a/(BQ). Направление, в котором закручивается спираль, зависит от знака заряда частицы. Если скорость v заряженной частицы составляет угол a с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.
|

 .
. Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I 1 и I 2 (направления токов указаны на рис.167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I 1 на элемент dl второго проводника с током I 2.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I 1 и I 2 (направления токов указаны на рис.167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I 1 на элемент dl второго проводника с током I 2. .
.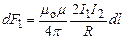 .
.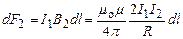 .
.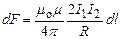 .
.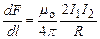 .
.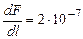 Н / м. Подставив это значение, получим
Н / м. Подставив это значение, получим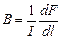 .
. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q >0 направления I и v совпадают, для Q<0 - противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис.169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца равен F=QvB sin α, где α - угол между v и В.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q >0 направления I и v совпадают, для Q<0 - противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис.169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца равен F=QvB sin α, где α - угол между v и В.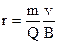 .
. Период вращения частицы., т. е. время Т, затрачиваемое ею на один полный оборот, T =2p r / v.
Период вращения частицы., т. е. время Т, затрачиваемое ею на один полный оборот, T =2p r / v. ,
, ;
; по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (в данном случае надо заменить v на
по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (в данном случае надо заменить v на 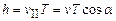 . Подставив в последнее выражение, получим
. Подставив в последнее выражение, получим


