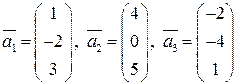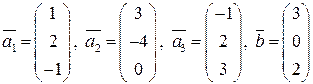ТИПОВОЙ РАСЧЕТ ПО ДИСЦИПЛИНЕ
Нередко отношение родителя к подростку обусловливается не действительными особенностями подростка, а теми чертами, которые родитель приписывает его полу, т. е. «вообще мужчинам» или «вообще женщинам». Так, при наличии предпочтения женских качеств наблюдается неосознаваемое непринятие подростка мужского пола. В таком случае приходится сталкиваться со стереотипными отрицательными суждениями о мужчинах вообще: «Мужчины в основном грубы, неопрятны. Они легко поддаются животным побуждениям, агрессивны и чрезмерно сексуальны, склонны к алкоголизму. Любой же человек, будь то мужчина или женщина, должен стремиться к противоположным качествам — быть нежным, деликатным, опрятным, сдержанным в чувствах». Именно такие качества родитель с ПЖК и видит в женщинах. Примером проявления установки ПЖК может служить отец, видящий массу недостатков у сына и считающий, что таковы и все его сверстники. В то же время этот отец «без ума» от младшей сестры подростка, так как находит у нее одни достоинства. Под влиянием ПЖК в отношении подростка мужского пола в данном случае формируется тип воспитания «эмоциональное отвержение». Возможен и противоположный перекос с выраженной антифеминистской установкой, пренебрежением к матери подростка, его сестрам. В этих условиях по отношению самого подростка мужского пола может сформироваться воспитание по типу «потворствующей гиперпротекции».
Типичные ошибки семейного воспитания — действия (бездействия), которые осуществляют родители в интересах воспитания ребенка. При этом сами родители негативной роли «воспитательной деятельности» не осознают или делают вид, что не осознают. К таким ошибкам относятся: • недооценка роли личного примера родителей; • отсутствие единства требований в воспитательной деятельности родителей; • отстранение детей от посильного домашнего труда; • неумение пользоваться методами воспитания, особенно поощрением и наказанием; • применение физического наказания; • отсутствие такта в отношении с ребенком; • ссоры родителей в присутствии детей; • неправильное поведение отдельных родителей в быту (пьянство, скандалы); • переоценка родителями своих воспитательных возможностей; • неоправданная идеализация своих детей («мой ребенок самый умный, талантливый, необыкновенный») и т.п. ТИПОВОЙ РАСЧЕТ ПО ДИСЦИПЛИНЕ «ЛИНЕЙНАЯ АЛГЕБРА» (Часть 1. Линейные и евклидовы пространства)
Направление 080100 «Экономика»
Очная форма обучения
Рязань 2012 Вариант 1 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 2 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 6 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 7 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 9 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 10 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 11 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 12 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 16 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 17 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов
Вариант 19 Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы
Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений
Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов 1. Доказать, что она является базисом в пространстве 2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве
|



 .
. , написать матрицу
, написать матрицу  перехода от стандартного базиса
перехода от стандартного базиса  пространства
пространства  .
. в базисе
в базисе  ,
, 
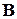 , если в
, если в 
 ,
,  пространства
пространства 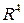 и дополнить эти векторы до ортогонального базиса
и дополнить эти векторы до ортогонального базиса






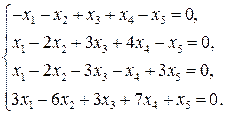




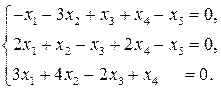
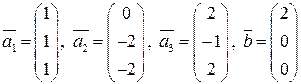

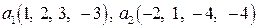
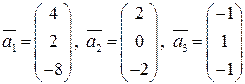













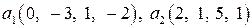








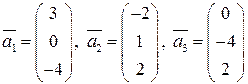

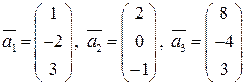



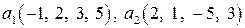

 ,
,
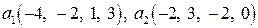


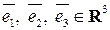 пространства
пространства 


 .
.


 в базисе
в базисе 






 пространства
пространства 
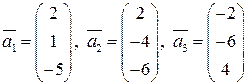
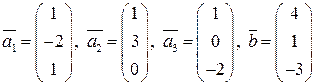
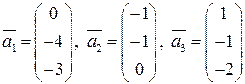



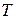 перехода от стандартного базиса
перехода от стандартного базиса 
 ,
, 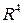 и дополнить эти векторы до ортогонального базиса
и дополнить эти векторы до ортогонального базиса


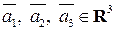 .
. , написать матрицу
, написать матрицу 
 , если в
, если в