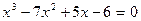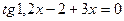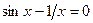Неравенства с одной переменной. Теоремы о равносильности неравенств.
Замінимо рівняння Ітераційна послідовність може бути як збіжною, так і розбіжною. Теорема збіжності ітераційної послідовності. Нехай рівняння 1) 2) 3) існує таке дійсне Тоді ітераційна послідовність Перетворення рівняння до ітераційного вигляду Рівняння З цією метою рівняння Таблиця 1
Контрольні запитання 1. Які існують методи відокремлення коренів та їх уточнення? 2. Як зробити оцінку вибору функції? 3. В чому полягає суть методів простих ітерацій, Ньютона, бісекцій та їх геометрична інтерпретація? 4. Поясніть схему алгоритму та програму відшукання коренів нелінійних рівнянь методами простих ітерацій, Ньютона, бісекцій. Неравенства с одной переменной. Теоремы о равносильности неравенств.
Рассмотрим два выражения, из которых хотя бы одно содержит переменную. Пусть это будут выражения х + 2 и 6. Соединив их знаками неравенства < или >, получим предложение х + 2 < 6. Это предложение содержит переменную и при подстановке вместо переменной конкретных числовых значений обращается в числовое неравенство (высказывание) истинное или ложное. Таким образом, предложение х + 2 < 6 есть высказывательная форма или предикат с одной переменной. Такой предикат называют неравенством с одной переменной. В общем случае понятие неравенства с одной переменной можно определить так. Опр. 1. Пусть f (x) и g (x) - два выражения с переменной x Одноместный предикат вида f (x) < g (x) называется неравенством с одной переменной. Опр. 2. Решением или корнем неравенства с одной переменной называется всякое значение переменной, которое обращает данное неравенство с переменной в истинное числовое неравенство. Решить неравенство - значит найти множество его решений. Иначе говоря, решить неравенство - значит найти область истинности Т данного предиката. При этом следует помнить, что область истинности предиката всегда является подмножеством его области определения. Следовательно, множество Т решений неравенства f (x) < g (x) является подмножеством множества X, то есть Т Ì Х. Например, неравенство x + 2 < 6 имеетмножество решений x < 4, то есть его множество решений Т= (-∞; 4). Для того, чтобы найти решения неравенства, его, как правило, преобразовывают до тех пор, пока не получат неравенство, решения которого находятся известным способом. Но чтобы найденные решения были решениями данного неравенства, необходимо преобразования неравенства выполнять по определенным правилам. При этом используют понятие равносильности неравенства. Опр. 3. Два неравенства f (x) < g (x) (1) и j (x) < k (x), (2) рассматриваемые на множестве X, называются равносильными, если множества их решений равны.
Например, неравенства x + 2 < 6, 2 x + 4 < 12 и 4 - x > 0 равносильны на множестве действительных чисел R, так как множества их решений Т= (-∞; 4) равны. Теорема 1. Пусть неравенство f (x) < q(х) (1) задано на множестве X и h(х) – выражение c переменной, определенное на том же множестве X. Тогда неравенства f (x) < q(х) (1) и f (x) + h(х) < q(х) + h(х) (2) равносильны на множестве X. Доказательство. Обозначим множество решений неравенства (1) через Т1, а множество решений неравенства (2) через Т2. Чтобы убедиться в равносильности неравенств (1) и (2), достаточно показать, что Т1 = Т2, то есть Т1 Ì Т2 и Т2 Ì Т1. 1. Пусть а - произвольное решение неравенства (1). Тогда аÎТ1 и при подстановке в неравенство (1) обращает его в истинное числовое неравенство f(а) < q(а), а выражение h(х) обращается в числовое выражение h(а). К обеим частям истинного числового неравенства f(а) < q(а) прибавим числовое выражение h(а). По свойству 1 истинных числовых неравенств получим истинное числовое неравенство f(а) + h(а) < q(а) + h(а). Но это означает, что а является решением неравенства (2), т. е. аÎТ2. В силу произвольности выбора решения а можем утверждать: всякое решение неравенства (1) является решением неравенства (2), то есть Т1 Ì Т2. 2. Пусть теперь b - произвольное решение неравенства (2). Тогда b Î Т2 и при подстановке в неравенство (2) обращает его в истинное числовое неравенство f(в) + h(в) < q(в) + h(в). К обеим частям этого неравенства прибавим числовое выражение – h(в). По свойству истинных числовых неравенств получим истинное числовое неравенство f(в) < q(в). Это означает, что в является решением неравенства (1). Поскольку решение в выбрано произвольно, можно утверждать, что каждый корень неравенства (2) является корнем неравенства(1), то есть Т2 Ì Т1. Из того, что Т1 Ì Т2 и Т2 Ì Т1, по определению равных множеств следует, что Т1 = Т2 и равносильность неравенств (1) и (2) доказана. Из доказанной теоремы вытекают важные следствия.
Следствие 1. Если к обеим частям неравенства прибавить одно и то же число, то получим неравенство, равносильное данному. Следствие 2. Если какое-либо слагаемое перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.
Теорема 2. Пусть неравенство f(x) < q(х) (1) задано на множестве X и h(х) – выражение c переменной, определенное на том же множестве X и принимающее положительные значения при всех значениях переменной из множества X. Тогда неравенства f(x) < q(х) (1) и f(x) ∙ h(х) < q(х) ∙ h(х) (2) равносильны на множестве X. Теорема 3. Пусть неравенство f(x) < q(х) (1) задано на множестве X и h(х) – выражение c переменной, определенное на том же множестве X и принимающее отрицательные значения при всех значениях переменной из множества X. Тогда неравенства f(x) < q(х) (1) и f(x) ∙ h(х) > q(х) ∙ h(х) (2) равносильны на множестве X.
Доказательство этих теорем аналогично доказательству теоремы 1. Из теорем 2 и 3 также вытекают важные следствия.
Следствие из теоремы 2. Если обе части неравенства умножить (или разделить) на одно и то же положительное число, то получим неравенство, равносильное данному с тем же знаком. Следствие из теоремы 3. Если обе части неравенства умножить (или разделить) на одно и то же отрицательное число, то получим неравенство, равносильное данному с противоположным знаком.
|

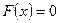 рівносильним рівнянням
рівносильним рівнянням  . Нехай
. Нехай  - корінь цього рівняння, а
- корінь цього рівняння, а  - одержане будь-яким способом початковим наближенням до кореня
- одержане будь-яким способом початковим наближенням до кореня  у праву частину рівняння, одержимо деяке число
у праву частину рівняння, одержимо деяке число  . Зробимо те ж саме з
. Зробимо те ж саме з  , одержимо
, одержимо  і так далі. Використовуючи крок за кроком співвідношення
і так далі. Використовуючи крок за кроком співвідношення  для
для  одержуємо числову послідовність
одержуємо числову послідовність  ,…., яку називають ітераційною послідовністю.
,…., яку називають ітераційною послідовністю. і виконані умови:
і виконані умови: визначена і диференційована на
визначена і диференційована на  для всіх
для всіх  ;
; , що
, що  для всіх
для всіх  .
. .
. виконувались умови теореми збіжності.
виконувались умови теореми збіжності. ,
,  де стала
де стала  . Тоді позначимо
. Тоді позначимо  Диференціюючи, отримуємо
Диференціюючи, отримуємо 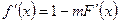 . Для виконання умови 3 теореми збіжності потрібно
. Для виконання умови 3 теореми збіжності потрібно  . А для цього досить підібрати сталу
. А для цього досить підібрати сталу  Підставимо це значення
Підставимо це значення  у рівняння
у рівняння