Регулировочная характеристика ТРН при активно-индуктивном характере нагрузки
Наличие индуктивности в цепи нагрузки вносит отличие в характер изменения тока нагрузки и напряжения. Действующее значение напряжения нагрузки определяются по формуле
В относительных единицах
Ток в нагрузки на интервале проводимости каждого тиристора ψ находят из анализа переходного процесса, обусловленного отпиранием тиристора. Его можно определить в виде суммы двух составляющих: принужденной и свободной. Принужденная составляющая тока i нг.пр. отстает на угол φ=arctg(ωLнг./Rнг.) от напряжения питания питающей сети u. Принужденная составляющая тока определяется по формуле (185).
Свободная составляющая тока нагрузки спадает по экспоненциальному закону:
с постоянной времени τ= L нг/ R нг=tgφ/ω. (187) В момент времени υ=α сумма принужденной и свободной составляющих, определяющая ток iнг, равна нулю:
откуда определяем коэффициент А:
С учетом выражения (184) и (185)находим
Рисунок 42. Временные диаграммы, иллюстрирующие работу преобразователя переменного напряжения при критическом значении угла управления
При чисто активной нагрузке (L нг=0, φ=0, tgφ=0) соотношение (189) приводится к виду
т.е. кривая тока i нг на интервале проводимости тиристоров определяется синусоидой напряжения питания (смотри рисунок 37,г). После подстановки в (189) значения υ=π+δ, соответствующего току i нг=0 (рисунок 38, б, в), получаем уравнение (190)
которое может быть использовано для определения угла δ. При активно - индуктивной нагрузке преобразователя представляет интерес определение так называемого критического значения угла управления α=αкр, при котором интервалы проводимости тока δ полностью занимают интервалы α. В этом случае (рисунок 42) ток i нг спадает до нуля в момент времени υ=π+δ (т. е. момент запирания одного тиристора совпадает во времени с моментом отпирания другого тиристора), паузы в кривой тока i нг и напряжения U нг отсутствуют и длительность проводящего состояния каждого тиристора ψ становится равной 180°. Из уравнения (190) следует, что такой режим имеет место при
Действующее значение напряжения на нагрузке максимально и относительная его величина согласно соотношению (184) равна единице. Кривая тока i нг становится непрерывной и синусоидальной. В соответствии с выражением (190) при α=αКР имеем
Очевидно, аналогичный режим работы будет и при углах αкр>α>0. Диапазон углов α от нуля до αкр характеризует неуправляемую зону преобразователя, где изменение угла α не вызывает изменения действующего значения напряжения на нагрузке и ее тока. Для осуществления нормальной работы схемы в этой зоне (создания непрерывного тока нагрузки) необходимо подавать на тиристоры управляющие импульсы достаточной длительности (рисунок 42), чтобы при малых углах α< αкр они перекрывали по длительности момент перехода тока нагрузки через нуль. В противном случае отпирающий импульс для очередного тиристора закончится раньше, чем прекратится ток в параллельном ему тиристоре, и тиристор не сможет открыться — произойдет пропуск его отпирания. Исходя из наименьшего угла α=0 длительность отпирающих импульсов должна, быть не меньше φ.
Вопросы для самоконтроля: 1 Приведите выражение регулировочной характеристики тиристорного регулятора переменного напряжения при чисто активной нагрузке. 2 Приведите выражение внешней характеристики тиристорного регулятора переменного напряжения. 3 Укажите в чем отличия в работе тиристорного регулятора переменного напряжения при чисто активной и активно-индуктивной нагрузке.
|


 (184)
(184) (185)
(185) (186)
(186)
 (188)
(188) (189)
(189)
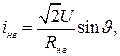
 , (190)
, (190) (191)
(191) (192)
(192)


