Напряженность электрического поля неподвижного точечного заряда
где Q – источник поля. Зависимость E (r) дана на рис. 11.2.
Рис.11.1. Зависимость модуля вектора напряженности электрического поля точечного заряда от расстояния Картины линий напряженности ("силовых линий") электрического поля точечных зарядов даны на рис. 9.4 и 9.5. Формулу (11.2) для электрической силы, действующей между двумя точечными зарядами можно будет записать в виде
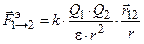 . (11.4) . (11.4)
Здесь Q1 и Q2 - алгебраические величины (см.9.2.2.).
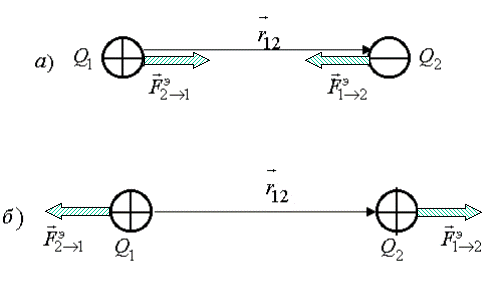
Рис.11.2.Электрическое взаимодействие точечных зарядов: а) разноименных (притяжение); б) одноименных (отталкивание).
Формула (11.4) выражает закон Кулона – электрическую силу взаимодействия двух точечных зарядов (этот закон по форме аналогичен закону всемирного тяготения – см.(10.4)). Электрическая сила, действующая со стороны заряда 1 на заряд 2,
в случае притяжения разноименных зарядов (рис.11.2, а), и электрическая сила, действующая со стороны заряда 1 на заряд 2,
в случае отталкивания одноименных зарядов (рис.11.2, б). Силовая (векторная) характеристика электрического поля
где gradj (градиент потенциала) – вектор, направленный в сторону быстрейшего увеличения потенциала поля (см. рис.11.3). Потенциал поля точечного заряда q:
где Q может быть положительным (>0) и отрицательным (<0). Формула (11.5) может быть выведена по аналогии с выводом формулы (10.8) потенциала гравитационного поля точечной массы (гл.10). Зависимости j(r) представлены на рис. 11.3.
Рис. 11.3. Зависимость потенциала поля Скалярной характеристикой взаимодействия в электрическом поле является потенциальная энергия, величина которой может быть получена на основе взаимосвязи силы и потенциальной энергии (10.9). Тогда, например, потенциальная энергия взаимодействия (отталкивания) двух одно именных точечных зарядов будет равна:
а потенциальная энергия взаимодействия (притяжения) двух разно именных точечных зарядов будет равна:
|

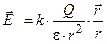 , (11.3.)
, (11.3.)
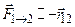
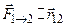
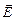 и энергетическая (скалярная) характеристика поля j связаны друг с другом соотношением (табл.9.1):
и энергетическая (скалярная) характеристика поля j связаны друг с другом соотношением (табл.9.1):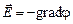 ,
,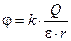 ,(11.5)
,(11.5)
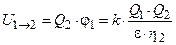 , (11.6)
, (11.6) .(11.7)
.(11.7)


