Магнитное поле движущегося заряда (в вакууме)
Как было показано выше, движущийся электрический заряд создает и электрическое и магнитное поля (единое электромагнитное поле). Силовая характеристика магнитного поля – индукция Поэтому индукция магнитного поля движущегося в веществе точечного заряда
При b ® 0
Силовая линия магнитного поля строится так, чтобы в каждой точке силовой линии вектор  был направлен по касательной к этой линии (рис. 11.9 и рис. 11.10). Силовые линии магнитного поля замкнуты. Магнитное поле - вихревое, непотенциальное. был направлен по касательной к этой линии (рис. 11.9 и рис. 11.10). Силовые линии магнитного поля замкнуты. Магнитное поле - вихревое, непотенциальное.
Рис. 11.9. Электромагнитное поле движущегося точечного заряда
Рис. 11.10. Вихревой характер магнитного поля положительного заряда, движущегося «от читателя». 11.6.Закон Био – Савара – Лапласа Закон Био – Савара – Лапласа определяет магнитное поле элемента тока. Введем понятие элемента тока:
По аналогии с магнитным полем движущегося точечного заряда индукция магнитного поля элемента тока в вакууме (рис. 11.11) выражается:
– закон Био – Савара – Лапласа в векторной и скалярной формах, соответственно.
Рис. 11.11. Магнитное поле элемента тока 11.7.Магнитное взаимодействие Рассмотрим токи в металлических проводниках. Вокруг металлического проводника нет суммарного электрического поля, так как электрические поля катионов и свободных электронов взаимно компенсируют друг друга и остается только магнитное поле, создаваемое движущимися электронами*. Магнитная сила, действующая на заряд q 2 во втором проводнике со стороны магнитного поля B 1 первого проводника (рис. 11.12), равна
Если
и измеряется в Н/м.
Рис. 11.12. Магнитное взаимодействие параллельных токов:
11.8.Электромагнитное взаимодействие потоков
Рассмотрим действие заряда q 1, движущегося со скоростью v1 << c,на движущийся со скоростью v2 заряд q 2. Заряд q 1 создает электрическое поле напряженностью
и магнитное поле
Поэтому заряд q 2 испытывает действие электрической силы
и магнитной силы
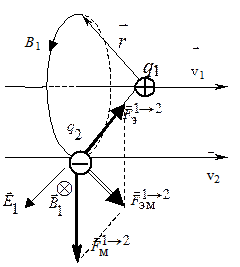
В результате на заряд q 2 действует электромагнитная сила Лоренца (рис. 11.13)
Рис. 11.13. Электромагнитное взаимодействие
|

 соотношением (11.14).
соотношением (11.14). (11.15.)
(11.15.) . (11.16.)
. (11.16.)

 . (11.17)
. (11.17) (11.18)
(11.18)
 (11.19.)
(11.19.)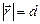 , то приведенная магнитная сила (сила, отнесенная к единице длины проводника) равна
, то приведенная магнитная сила (сила, отнесенная к единице длины проводника) равна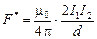 (11.20.)
(11.20.)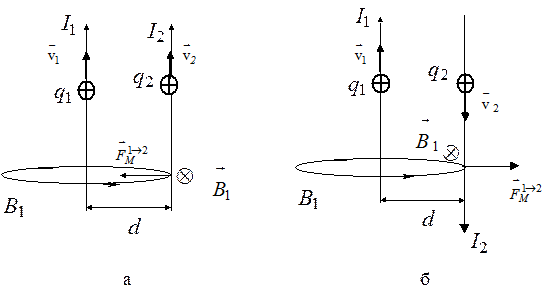
 (11.21)
(11.21)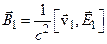 .(11.22)
.(11.22) (11.23)
(11.23) .(11.24)
.(11.24)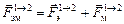 .(11.25)
.(11.25)